Пример метода золотого сечения

Опять рассмотрим задачу из примера 2.6, в которой требуется минимизировать f(х)=(100- х)² в интервале 60£ х £150. Для того чтобы перейти к интервалу единичной длины, проведем замену переменной, положив w=(х - 60)/90. Таким образом, задача принимает следующий вид: минимизировать f(w) = (40 – 90 w)² при ограничении 0£w£1.

Итерация 1. I₁ = (0, 1); L₁ = l. Проведем два первых вы­числения значений функции:

w₁ = t = 0,618, f(w₁) = 244,0

w₂ = 1- t = t ² = 0,382, f(w₂) = 31,6

Так как f(w₂) < f(w₁) и w₂ < w₁, интервал w ³ w₁ исключается.

Итерация 2. I₂ =(0. 0,618); L₂ = 0,618 = t. Следующее вы­числение значения функции проводится в точке

w₃ = t-t² = t(1-t) = t³ = 0,236, f(w₃) = 352.

Так как f(w₃) > f (w₂) и w₃ < w₂, интервал w £ w₃, исключается.

Итерация 3. I₃ =(0,236, 0,618); L₃ = 0,382 = t². Следующее вычисление значения функции проводится в точке, расположенной на расстоянии t ´ (длина полученного интервала) от левой гра­ничной точки интервала, или на расстоянии (1- t) ´ (длина ин­тервала) от правой граничной точки. Таким образом,

w₄ =0,618 – ( 1- t)L₃ = 0.618 - t² L₃ 0.618 - t²(t²) = 0.618 - t⁴ = 0,472, f(w₄) = 6,15.

Так как f(w₄) < f (w₂) и w₄ > w₂, интервал w £ w₂ исключается.

В результате получен следующий интервал неопределенности: 0,382 £ w £ 0,618 для переменной w, или 94,4£ х £115,6 для перемен­ной х.

Если в процессе поиска проведено шесть вычислений значений функции, то длина результирующего интервала для переменной w равна

t_N-1 = t₅ = 0,09,

что соответствует интервалу длины 8,1 для переменной х. Для срав­нения напомним, что в аналогичной ситуации метод деления интер­вала пополам привел к получению интервала длины 11,25.

В общем случае если правая и левая граничные точки интервала неопределенности (обозначим их через XR и XL) известны, то ко­ординаты всех последующих пробных точек, получаемых в соответ­ствии с методом золотого сечения, можно вычислить по формулам

w = XR - tⁿ или w = XL + tⁿ, в зависимости от того, какой подынтервал был исключен на преды­дущей итерации – левый или правый. В приведенных выше форму­лах через tⁿ обозначена n -я степень t, где п – количество вычисле­ний значений функции.

Поиск с помощью метода золотого сечения может быть окончен либо исходя из заданного количества вычислений значений функ­ции (и, следовательно, величины интервала неопределенности), либо по достижении относительной точности искомого значения функции. Наиболее предпочтительным является использование обоих критериев одновременно.

Сравнение методов исключения интервалов. Ниже проводится сравнение относительных эффективностей рас­смотренных методов исключения интервалов. Обозначим длину неходкого интервала неопределенности через L₁, а длину интервала, получаемого в результате N вычислений значений функции, - через L_N. В качестве показателя эффективности того или иного метода исключения интервалов введем в рассмотрение характеристику относительного уменьшения исходного интервала FR(N)=L_N/L₁

Напомним, что при использовании метода деления интервала пополам и метода золотого сечения длина получаемого интервала составляет L₁(0,5)^N/2 и L₁(0.618)^N-1 соответственно. Следовательно, относительное уменьшение интервала после N вычислений значений функции равно

FR(N) = (0,5)^N/2 для метода деления интервала пополам;

FR(N) = (0,618) ^N-1 для метода золотого сечения.

Для сравнения рассмотрим также метод равномерного поиска, в соответствии с которым оценивание функции проводится в N равноотстоящих друг от друга точках (при этом интервал L₁ де­лится на (N+1) равных интервалов длины L₁/(N+l)). Пусть х* – точка, в которой наблюдается минимум функции f(х). Тогда точка истинного минимума f(x) оказывается заключенной в интервале

 

,

 

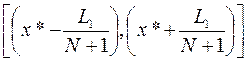откуда L_N = 2L₁/(N+l). Следовательно, для метода равномерного поиска FR(N)=2/(N+1).

В табл. 6.2 представлены значения FR(N), соответствующие выбранным N, для трех методов поиска. Из таблицы следует, что поиск величины относительного уменьшения интервала с помощью метода золотого сечения

 

Таблица 6.2

Метод поиска	Количество вычислений значений функции
N=2	N=5	N=10	N=15	N=20
Метод деления интервала пополам	0,5	0,177	0,031	0,006	0,0009
Метод золотого сечения	0,618	0,146	0,013	0,001	0,0001
Метод равномерного поиска	0,667	0,333	0,182	0,125	0,095

 

обеспечивает наибольшее от­носительное уменьшение исходного интервала при одном и том же количестве вычислений значений функции. С другой стороны, можно также сравнить количества вычислений значения функции, требуе­мые для достижения заданной величины относительного уменьшения интервала или заданной степени точности. Если величина FR(N) = E задана, то значение N вычисляется по следующим формулам:

для метода деления интервала пополам

N=2 ln(E)/ln(0,5),

для метода золотого сечения

N=1+[ln(E)/ln(0,618)],

для метода равномерного поиска

N=(2/E)-1

В табл. 6.3 приведены данные о количествах вычислений значений функции, необходимых для определения координаты точки мини­мума с заданной точностью. Следует еще раз подчеркнуть, что метод золотого сечения оказывается более эффективным по сравнению с остальными двумя методами, поскольку он требует наименьшего числа оцениваний значения функции для достижения одной и той же заданной точности.

Требуемые количества вычислений значений функции

Таблица 6.3

Метод поиска	Заданная точность
Е=0,1	Е=0,05	Е=0,01	Е=0,001
Метод деления интервала пополам
Метод золотого сечения
Метод равномерного поиска

 

Критерии оптимизации

 

Важная сторона оптимизации – это выбор критерия, по которому определяются свойства объекта и который позволяет количественно оценить какое из устройств данного класса является наилучшим.

Критерии в зависимости от назначения устройства могут быть самыми разными.

Так при проектировании фильтра критерий может относиться к его амплитудно-частной характеристике, минимуму потерь в полосе прозрачности и максимуму – в полосе заграждения.

В случае усилителя высокочастотных колебаний такой критерий может быть связан с получением максимального КПД, с соблюдением требования по нелинейным искажениям сигнала.

Несмотря на все разнообразие критериев их можно свести к единой математической записи – функции цели, которая в концентрированной форме отражает смысл решаемой задачи по оптимизации устройства – в наилучшем приближении его характеристик к требуемым согласно определенным признакам.

Все действия в такой программе оптимизации в конечном итоге направлены на получение экстремального значения функции цели – максимального или минимального, в зависимости от поставленной задачи.

Поскольку, как правило, качество устройства определяют несколько критериев (например, в приводимом выше примере с фильтром – максимум в одной полосе, минимум – в другой), то целевая функция является суммой определенного числа членов и по своему виду является взвешенно-аддитивно цифровой, отражающей требование минимального отличия желаемых (иногда идеальных) характеристик от реально получаемых. Составим в обобщенном виде функцию цели.

При исследовании в частотной области для целевой функции, определяемой K критериями, запишем:

 

(6.5)

 

где Ф_k – частная целевая функция для k-й характеристики;

ψ_kT – функция, определяющая требуемую k-ю частотную характеристику;

ψ_kP – функция, определяющая реально полученную k-ю частотную характеристику, зависящую от параметров устройства;

V_k – весовой множитель для k-й характеристики.

Мерой расхождения между требуемой и реальной характеристиками могут являться или минимум суммы квадратов уклонений, или минимаксный критерий. При них функция цели примет вид:

 

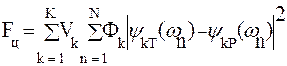(6.6)

 

(6.7)

Кроме того возможен вариант, когда требуется получить максимальное отношение параметров устройства, например A_k к B_k. Тогда функция цели примет вид:

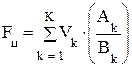(6.8)

 

Путем определенной процедуры следует найти или минимальное при (6.6) и (6.7), или максимальное при (6.8) значение функции цели. Для определенности рассмотрим первый случай, связанный с получением минимального значения.

Разделим все параметры устройства, определяющие его реальную характеристику ψ_kP, на две группы: варьируемые (x₁,x₂,…,x_n) и неизменные (y₁,y₂,…,y_m). Соберем варьируемые параметры (их еще называют переменными) в вектор-столбец, который затем преобразуем в транспонированную матрицу:

 

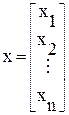
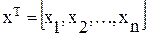(6.9)

 

Аналогичным образом поступим с постоянными или неизменными параметрами устройства:

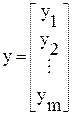
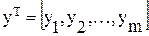(6.10)

Будем рассматривать вектор x как точку или элемент n-мерного действительного пространства Rⁿ . Совокупность объектов x произвольного содержания (точки, векторы, функции и т.д.) составляют множество X, а сами объекты есть элементы этого множества. Совместив понятия точечного множества, составленного из точек х, и n-мерного пространства Rⁿ , можно утверждать, что множество X представляет собой совокупность точек х в многомерном пространстве Rⁿ .

В процессе поиска среди множества векторов x следует найти такой вектор X_опт в пространстве Rⁿ , при котором функция цели (6.6) или (6.7) минимальна:

 

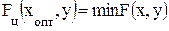_, где x Є Rn (6.11)

 

При этом на вектор х могут накладываться определенные ограничения. Точка x_опт соответствует наилучшему в соответствии с выбранными критериями варианту проектируемого устройства. Поиск x_опт относится к классу задач, объединяемых теорией нелинейного программирования. При этом вектор х во всех рассматриваемых ниже задачах ограничен определенным пространством Rⁿ , что можно следующим образом представить в развернутом виде:

 

x_1мин ≤ x₁ ≤ x_1макс, ……….x_n.мин ≤ x_n.макс (6.12)

 

При функции цели в виде (6.8) выражение (6.11) примет вид:

 

F_ц (x_опт,y)=maxF(x,y), где x Є Rn (6.13)

 

Перейдем к рассмотрению путей нахождения x_опт.

13.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: