 |
Пример циклического расчета
|
|
|
|
Рассчитать с «шагом»  затухающий колебательный процесс, описываемый функцией:
затухающий колебательный процесс, описываемый функцией:
 ,
,
при А = 10, α = 0,5, F = 10 и N = 1000.
Организуем цикл расчета с помощью записи k:= 0…N и выражений для аргумента tk и дискретной функции Yk(tk), полученной из непрерывной функции Y(t).

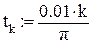

Строим график дискретной функции  :
:

Рис.6.36 График дискретной функции 
Вывод в виде таблицы дискретных значений  осуществляется путем записи Y= или
осуществляется путем записи Y= или  .
.
По умолчанию на рабочий лист выводится 16 значений функции.
Щелкнув по графику функции, обрамляют ее рамкой и путем протаскивания вниз курсора расширяют таблицу до любого требуемого значения k≤N.
При протаскивании курсора вверх таблица наоборот сжимается.
Таким же образом можно вывести и таблицу значений аргумента, сделав в рассматриваемом случае запись  .
.
7.
Обработка данных
Обработка данных – это важная сфера применения компьютерной математики.
При решении многих задач в радиотехнике, исходная функция задается в табличной форме или по точкам (например, экспериментально полученные амплитудная или амплитудно-частотная характеристики усилителя). Вместе с тем, для дальнейшего анализа необходимо знать значение функции при любом значении аргумента, а не только при некоторых его конкретных значениях. Данной цели, т.е. к переходу от дискретного описания функции к непрерывному, служит процедура аппроксимации. При определении функции между узловыми точками аппроксимация называется интерполяцией, а за их пределами – экстраполяцией.
«MathCAD» располагает двумя способами интерполяции:
· кусочно-линейной;
· сплайновой (более точная).
Кусочно-линейная интерполяция
|
|
|
При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости.
Для этого используется функция linterp (VX, VY, x). Для заданных векторов VX и VY узловых точек и заданного аргумента x функция linterp (VX, VY, x) возвращает значение функции при ее линейной аппроксимации. Графически это означает просто соединение узловых точек отрезками прямых. При экстраполяции используются отрезки прямых, проведенных через две крайние точки.
Пример
Пусть экспериментально получена амплитудная характеристика усилителя (таблица 6.1)
Таблица 6.1
| Uвх(В) | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | |
| Uвых(В) | 0.001 | 0.1 | 0.2 | 0.4 | 0.5 | 0.55 | 0.57 | 0.575 |
В программной среде «MathCAD» исходная функция (UВЫХ=F(UВХ)) записывается в виде матрицы [2x8]:

Далее производится сортировка значений функции по возрастанию значений аргумента, если в таблице такая сортировка не произведена. Для этого обращаемся к встроенным функциям f(x), (например, на стандартной линейке).
Записываем:
V:=
Открываем окно f(x) и выбираем в разделе категория функций – «сортировка», а в разделе имя функции – «сортировка по аргументу» (csort (v, o)).
После щелчка на кнопке «ок» получим запись:
 ,
,
далее вставляем имя матрицы:
V:= csort (V,0)
Далее присваиваем значениям аргумента значения из первого столбца:
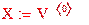 ,
,
а значениям функции значения второго столбца:

Теперь можно провести кусочно-линейную интерполяцию.
Записываем:
W(x):=
Открываем окно встроенных функций. В разделе «категория функций» указываем название «интерполяция», а в разделе «имя функции» – «линейная» («linterp»). После щелчка по клавише «ок» появляется запись:

Вводим в скобки последовательно X,Y,x:
W(x):= linterp(X,Y,x)
Далее по правилам построения графиков строим зависимость W(x) = f(x) (Рис. 6.38).

Рис.6.37 График зависимости W(x) = f(x)
|
|
|
Сплайн-интерполяция
Часто хорошие результаты дает сплайн-аппроксимация отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были первая и вторая производные. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закрепленную в узловых точках (откуда и название аппроксимации: splaine – гибкая линейка). Для осуществления сплайн-аппроксимации система Mathcad предлагает следующие функции:
cspline (VX, VY) – возвращает вектор VS вторых производных при приближении в опорных точках отрезками кубических полиномов;
pspline (VX, VY) – возвращает вектор VS вторых производных при приближении к опорным точкам отрезками парабол;
lspline (VX, VY) - возвращает вектор VS вторых производных при приближении к опорным точкам отрезками прямой;
interp (VS, VX, VY, x) –возвращает значение функции y(x) для заданных векторов VS, VX, и значения x.
Сплайн-аппроксимация проводится в два этапа. Вначале с помощью функций cspline, pspline или lspline отыскивается вектор вторых производных функции y(x), заданной векторами VX и VY ее абсцисс и ординат. Затем для каждой точки вычисляется y(x) с помощью функции interp.
Сплайн интерполяции даже при небольшом количестве точек (5-6) дает хорошие результаты:
· график функции оказывается плавным;
· точки его перегиба незаметны.
Проведем сплайн-интерполяцию для рассмотренного выше примера.

V:= csort (V,0)

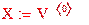
Этапы записи таблицы в виде матрицы и сортировки аналогичны кусочно-линейной интерполяции.
Далее записываем:
S:=
Открываем встроенные функции f(x) и в разделе «категория функций» выбираем «интерполяция», а в разделе «имя функции» - «cspline». После щелчка по клавише «ОК» появится
S:=cspline( ,
,  )
)
Вводим под знак cspline аргумент Х и функцию Y.
S:=cspline(X, Y)
Далее записываем:
W(x):=
Открываем встроенные функции f(x) и в разделе «категория функций» выбираем «интерполяция», а в разделе «имя функции» - «interp». После щелчка по клавише «ОК» появляется:
W(x):= interp( ,
,  ,
,  ,
,  ),
),
куда последовательно под знак функции вводятся обозначения S,X,Y,x.
W(x):= interp(S, X, Y, x).
Далее по правилам построения графиков строим в декартовой системе координат график функции W(x)= f(x) (Рис. 6.38).
|
|
|

Рис.6.38 График функции W(x)= f(x)
Экстраполяция
В математике экстраполяцией называется предсказание поведения некоторой зависимости по имеющимся измерениям ее характеристики в определенной, иногда довольно узкой области.
В MathCAD экстраполяция основывается на анализе поведения зависимости в нескольких точках.
Функцией, реализующей алгоритм линейной экстраполяции является встроенная функция
predict (y, m, n),
где y – вектор эмпирических значений экстраполируемой характеристики по оси ординат. Особенность алгоритма, используемого функцией, заключается в том, что экстраполяцию он делает только на основании y -координат выборки при постоянном шаге по оси абсцисс;
m – количество ближайших к правой границе выборки точек, на основании которых проводится экстраполяция;
n – количество точек в просчитываемом векторе прогноза.
При помощи функции «predict» можно проводить довольно эффективную экстраполяцию непрерывных, периодических или осциллирующих функций в относительно неширокой области.
Пример:
Предсказать поведение кривой затухающих колебаний.
Для этого зададим вектор из y-координат его 101-ой точкой на промежутке от 0 до 3 π. Шаг изменения переменной при определении вектора данных должен быть постоянным. Организуем вектор путем использования ранжированных переменных.




Далее зададим векторы экстраполяции при помощи функции «predict».
Чтобы сравнить степень влияния количества анализируемых точек выборки на качество предсказания, определим три экстраполяционных вектора при различных значениях параметра m. Размерность этих векторов определим, например, 150.



Строим графики векторов приближений (рис. 6.39).

Рис. 6.39 Графики векторов приближений
При этом переменная для векторов экстраполяции может быть определена прибавлением к вектору x соответствующей координаты крайнего значения в выборке (3π).
Из анализа графиков можно сказать, что функция «predict» довольно эффективна лишь на небольшом отрезке правой крайней точки выборки, что отсутствует прямая зависимость между обрабатываемым числом точек и точностью информации о продолжаемой кривой.
|
|
|
Успех экстраполяции зависит от типа исследуемой зависимости. Лучше всего удается предсказание поведения парабол, экспоненциальных кривых и несложных периодических функций.
Чем сложнее зависимость, тем короче интервал экстраполяции.
Если в выборке мало точек и шаг между ними велик, то экстраполяция бессмысленна.
8.
Символьные вычисления
Все математические вычисления можно отнести к двум типам, исходя из принципа их осуществления:
Первый, символьный или аналитический, известен с глубокой древности.
Второй, численный, получил широкое распространение только во второй половине 20 века.
Решение задач аналитически имеет массу преимуществ перед решением численным:
· ответ может быть вычислен без какой-либо погрешности;
· получение результата в виде алгебраического выражения открывает куда более широкие возможности для его последующего использования; (новые законы (физические) выводятся в результате символьного интегрирования или дифференцирования более простых или исторически более ранних уравнений);
· числовой результат, полученный в символьном виде, более понятен нам, чем десятичная дробь, получаемая численно.
Почему же символьные вычисления не очень широко распространены пока в компьютерной математике? Причины следующие:
1. Аналитическим решением обладает ограниченное число задач. (Так, например, чтобы найти корни уравнения в виде выражения, требуется выразить одну переменную через все остальные (или коэффициенты). Сделать же это можно только в том случае, если уравнение включает переменные невысокой степени и не содержит разнородных функций)
Численно же можно решить практически любое уравнение.
2. Возможности современных компьютеров в области аналитических вычислений все еще крайне ограничены. Дело в том, что такие задачи относятся к области применения технологий искусственного интеллекта. Компьютеры научились очень быстро считать, но творчески анализировать и создавать что-то принципиально новое на основании некоторого минимального базиса они не могут.
Символьный процессор MathCAD хорошо справляется только с теми математическими проблемами, в основу который можно положить четкий и конкретный алгоритм (например, дифференцирование или подстановка переменной).
Качество решения MathCAD основных задач символьной алгебры (требующих творческого поиска), например, упрощение выражений или разложение на множители можно считать удовлетворительным только с той оговоркой, что еще 17 летназад (до 1990 года) таких технологий не существовало в принципе.
|
|
|
В системе MathCAD – два альтернативных пути осуществления того или иного символьного преобразования:
· при помощи команд специального меню «Символические» (Symbolics), которое расположено в главном меню программы;
· с использованием операторов панели инструментов (рабочей панели) «Символика» (Symbolic).
Остановимся на принципиальных различиях при символических вычислениях в случае использования панели инструментов по сравнению с использованием меню.
Символьные операции, производимые при помощи панели «Символика» осуществляются не командами, а специальными операторами.
Ввести такой оператор можно очень просто, нажав на панели нужный пункт. Например, если необходимо решить уравнение, то следует выбрать пункт «Решить» (Solve):
■ solve, ■ →
Появится оператор, образованный ключевым словом, двумя маркерами и оператором символьного вывода.
На место левого маркера вводится уравнение, правого переменная, по которой оно должно быть решено.
Пример
Решить уравнение x2 – a = 0
Используя панель «Символика» запишем:
x2 – a solve, x →
Результат получим в виде вектора: 
Символьные преобразования, осуществляемые при помощи операторов панели «Символика» более наглядны, чем при использовании команд соответствующего меню.
Посмотрим на примерах отличия символьных преобразований при использовании панели и меню. Главное отличие – это то, что преобразования при помощи команд меню осуществляются MathCAD без учета определений и присваиваний, сделанных в документе выше.
При использовании же операторов панели «Символика» происходит подстановка определенных выше значений параметров.
Пример
Необходимо разложить в ряд функцию cos(ax + b), при a = 3 и b = 5.
Разложение в ряд при помощи команды меню «Символические» дает:

При использовании же операторов панели «Символика» происходит подстановка значений введенных параметров a и b:

Очевидно, что использование команд меню удобнее тогда, когда результат не нужно сохранять или использовать в дальнейших расчетах. В противном случае лучше применять операторы панели «Символика».
Однако меню «Символические» имеет ряд команд и настроек, которые не находят отражения на рабочей панели.
Одной из особенностей этого меню является наличие в нем подменю «вычислить» (Evaluate), отвечающего за проведение арифметических расчетов при помощи символьного процессора.
Состав подменю «Вычислить»:
| Символические | (Symbolically) |
| Плавающая точка | (Floating Point) |
| Комплексные | (Complex) |
Данное меню содержит три команды.
В первой строке располагается команда «Символически» (Symbolically), предназначенная для расчета значения некоторой функции или выражения в символьном виде. По своему назначению она полностью совпадает с оператором символьного вывода «→». Эта же команда может быть задействована нажатием сочетания клавиш [«Shift» + «F9»] (при этом вычисляемое выражение должно быть выделено).
Пример
Необходимо вычислить 
Нажав [Shift + F9] получим:
 ,
,
либо, используя оператор символьного вывода:

В меню «Символы», подменю «Расчеты» расположена команда «Плавающая точка» (Floating Point). С ее помощью можно получить численное значение некоторого выражения с нужной точностью.
Чтобы это сделать, необходимо выделить выражение и нажать данную команду. На экране появится специальное окно настройки «Вычисления с плавающей запятой» (рис. 6.40).

Рис. 6.40 Команда «Вычисления с плавающей запятой»
В строке «Floating Point Precision» необходимо задать уровень по шкале от 1 до 4000.
Примеры использования команды «Плавающая точка»: Найдем значение следующего выражения при различных уровнях точности:
 .
.
Floating Point Precision = 3:

Floating Point Precision = 15:

Floating Point Precision = 20:

Для обычных выражений увеличение уровня точности от 20 и выше не приводит к каким либо изменениям в ответе, поскольку числа с дробной частью при символьных расчетах отображаются только до 20-го знака после запятой. Однако уровень точности 4000 может понадобиться в том случае, если вы работаете с очень малыми величинами.
Арифметические расчеты с помощью символьного процессора могут быть полезны, если величина результата меньше параметра «Порог нуля» («Zero Threshold») закладки «Точность» («Tolerance») меню «Формат результата» («Result Format»).
В этом случае при использовании оператора численного вывода «=» в качестве ответа будет выдан ноль. Вычисление же символически даст правильный результат.
Пример
Точность результата при различных типах расчета.
«Порог нуля» («Zero Threshold») = 10-10

Использование команды «Плавающая точка»:
8,6602540378443864675 · 10-101
В меню «Символы», подменю «Рсчеты» расположена команда «Комплексные» (Complex), при помощи которой можно производить перевод различных форм записи комплексных чисел к стандартной (вида a + i · b).
Пример
 ;
;
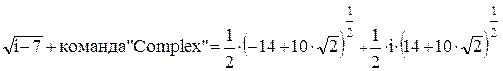 .
.
Произвести настройку особенностей отображения результата при использовании для символьных расчетов меню «Символические» (Symbolics) можно при помощи специального подменю «Стиль вычислений» (Evaluation Style) (рис. 6.41).

Рис 6.41 Подменю «Стиль вычислений»
При помощи параметров списка «Отображение шагов вычисления» (Show evaluations steps) рассматриваемого меню можно определить, каким образом по отношение к исходному выражению будет выведен результат символьных расчетов.
Данный список содержит 3 пункта:
1 «Вертикально, вставляя линии» (Vertikally, inserting lines). Параметр, определенный по умолчанию. Результат вставляется в специальную, очищенную от других формул полосу рабочей области ниже исходного выражения. Остальные объекты листа при этом смещаются вниз на ширину данной полосы;
2 «Вертикально, не вставляя линий» (Vertically, without inserting lines).
Результат выводиться ниже исходного выражения, но это не сказывается на положении других формул документа;
3 «Горизонтально» (Horizontally). Результат отображается правее исходного выражения.
Если поставить флажок в окошке «Вычислить на месте» (Evaluate In Place), то результат просто заменит исходное выражение.
При включении параметра «Показать комментарии» (Show comments) ответ выводиться на лист вместе с текстовой строкой, содержащей информацию о проделанной символьной операции.
Пример
x2 – 4x + 1, выделим х и проведем интегрирование. В результате выводятся комментарии и результат интегрирования:
by integration, yiecds

10.
|
|
|


