Числовые характеристики статистического распределения

В главе 5 мы ввели в рассмотрение различные числовые характеристики случайных величин:математическое ожидание, дисперсию, начальные и центральные моменты различных порядков. Эти числовые характеристики играют большую роль в теории вероятностей. Аналогичные числовые характеристики существуют и для статистических распределений. Каждой числовой характеристике случайной величины соответствует ее статистическая аналогия. Для основной характеристики положения — математического ожиданияслучайной величины – такой является среднее арифметическое наблюденных значений случайной величины:

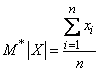, (7.4.1)

где — случайной величины, наблюденное -м опыте, - число опытов.

Эту характеристику мы будем в дальнейшем называть статистическим средним случайной величины.

Согласно закону больших чисел, при ограниченном увеличении числа опытов статистическое среднее приближается (сходится по вероятности) к математическому ожиданию. При ограниченном числе опытов статистическое среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем известное представление.

Подобные статистические аналогии существуют для всех числовых характеристик. Условимся в дальнейшем эти статистические аналогии обозначать теми же буквами, что и соответствующие числовые характеристики, но и снабжать их значком *.

Рассмотрим, например, дисперсию случайной величины. Она представляет собой математическое ожидание случайной величины :

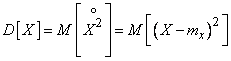. (7.4.2)

Если в этом выражении заменить математическое ожидание его статистической аналогией – средним арифметическим, мы получим статистическую дисперсию случайной величины :

, (7.4.3)

где 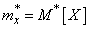- статистическое среднее.

Аналогично определяются статистические начальные и центральные моменты любых порядков:

(7.4.4)

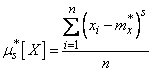(7.4.5)

Все эти определения полностью аналогичны данным в главе 5 определениям числовых характеристикслучайной величины, с той разницей, что в них везде вместо математического ожидания фигурирует среднее арифметическое. При увеличении числа наблюдений, очевидно, все статистические характеристики будут сходиться по вероятности к соответствующим математическим характеристикам и при достаточном могут быть приняты приближенно равными им.

Нетрудно доказать, что для статистических начальных и центральных моментов справедливы те же свойства, которые были введены в главе 5 для математических моментов. В частности, статистический первый центральный момент всегда равен нулю:

.

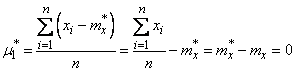Соотношения между центральными и начальными моментами также сохраняются:

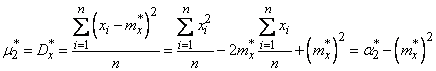(7.4.6)

и т.д.

При очень большом количестве опытов вычисление характеристик по формулам (7.4.1) - (7.4.5) становится чрезмерно громоздким и можно применить следующий прием: воспользоваться теми же разрядами, на которые был расклассифицирован статистический материал для построения статистического ряда или гистограммы, и считать приближенно значение случайной величины в каждом разряде постоянным и равным среднему значению, которое выступает в роли «представителя» разряда. Тогда статистические числовые характеристики будут выражаться приближенными формулами:

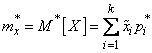, (7.4.7)

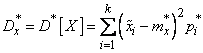, (7.4.8)

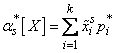, (7.4.9)

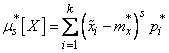, (7.4.10)

где — «представитель» -го разряда, - частота -го разряда, - число разрядов.

Как видно, формулы (7.4.7)— (7.4.10) полностью аналогичны формулам 5.6 и 5.7, определяющимматематическое ожидание, дисперсию, начальные и центральные моменты прерывной случайной величины , с той только разницей, что вместо вероятностей в них стоят частоты , вместо математического ожидания - статистическое среднее , вместо числа возможных значений случайной величины – число разрядов.

В большинстве руководств по теории вероятностей и математической статистике при рассмотрении вопроса о статистических аналогиях для характеристик случайных величин применяется терминология, несколько отличная от принятой в настоящей книге, а именно, статистическое среднее именуется «выборочным средним», статистическая дисперсия – «выборочной дисперсией» и т.д.

Происхождение этих терминов следующее. В статистике, особенно сельскохозяйственной и биологической, часто приходится исследовать распределение того или иного признака для весьма большой совокупности индивидуумов, образующих статистический коллектив (таким признаком может быть, например, содержание белка в зерне пшеницы, вес того же зерна, длина или вес тела какого-либо из группы животных и т.д.). Данный признак является случайной величиной, значение которой от индивидуума к индивидууму меняется. Однако, для того, чтобы составить представление о распределении этой случайной величины или об ее важнейших характеристиках, нет необходимости обследовать каждый индивидуум данной обширной совокупности; можно обследовать некоторую выборку достаточно большого объема для того, чтобы в ней были выявлены существенные черты изучаемого распределения. Та обширная совокупность, из которой производится выборка, носит в статистике названиегенеральной совокупности. При этом предполагается, что число членов (индивидуумов) в генеральной совокупности весьма велико, а число членов в выборке ограничено. При достаточно большом оказывается, что свойства выборочных (статистических) распределений и характеристик практически не зависят от ; отсюда естественно вытекает математическая идеализация, состоящая в том, что генеральная совокупность, из которой осуществляется выбор, имеет бесконечный объем. При этом отличают точные характеристики (закон распределения, математическое ожидание, дисперсию и т.д.), относящиеся к генеральной совокупности, от аналогичных им «выборочных» характеристик. Выборочные характеристики отличаются от соответствующих характеристик генеральной совокупности за счет ограниченности объема выборки ; при неограниченном увеличении , естественно, все выборочные характеристики приближаются (сходятся по вероятности) к соответствующим характеристикам генеральной совокупности. Часто возникает вопрос о том, каков должен быть объем выборки для того, чтобы по выборочным характеристикам можно было с достаточной точностью судить о неизвестных характеристиках генеральной совокупности или о том, с какой степенью точности при заданном объеме выборки можно судить о характеристиках генеральной совокупности. Такой методический прием, состоящий в параллельном рассмотрении бесконечной генеральной совокупности, из которой осуществляется выбор, и ограниченной по объему выборки, является совершенно естественным в тех областях статистики, где фактически приходится осуществлять выбор из весьма многочисленных совокупностей индивидуумов. Для практических задач, связанных с вопросами стрельбы и вооружения, гораздо более характерно другое положение, когда над исследуемой случайной величиной (или системой случайных величин) производится ограниченное число опытов с целью определить те или иные характеристики этой величины, например, когда с целью исследования закона рассеивания при стрельбе производится некоторое количество выстрелов, или с целью исследования ошибки наводки производится серия опытов, в каждом из которых ошибка наводки регистрируется с помощью фогопулемета, и т. д. При этом ограниченное число опытов связано не с трудностью регистрации и обработки, а со сложностью и дороговизной каждого отдельного опыта. В этом случае с известной натяжкой можно также произведенные опытов мысленно рассматривать как «выборку» из некоторой чисто условной «генеральной совокупности», состоящей из бесконечного числа возможных или мыслимых опытов, которые можно было бы произвести в данных условиях. Однако искусственное введение такой гипотетической «генеральной совокупности» при данной постановке вопроса не вызвано необходимостью и вносит в рассмотрение вопроса, по существу, излишний элемент идеализации, не вытекающий из непосредственной реальности задачи.

Поэтому мы в данном курсе не пользуемся терминами «выборочное среднее», «выборочная дисперсия», «выборочные характеристики» и т. д., заменяя их терминами «статистическое среднее», «статистическая дисперсия», «статистические характеристики».