Главная | Обратная связь | Поможем написать вашу работу!

Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения

Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определятьвероятность попадания случайной величины , подчиненной нормальному закону с параметрами , на участок от до . Для вычисления этой вероятности воспользуемся общей формулой

, (6.3.1)

где - функция распределения величины .

Найдем функцию распределения случайной величины , распределенной по нормальному закону с параметрами . Плотность распределения величины равна:

. (6.3.2)

Отсюда находим функцию распределения

. (6.3.3)

Сделаем в интеграле (6.3.3) замену переменной

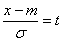
и приведем его к виду:

(6.3.4)

Интеграл (6.3.4) не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения или (так называемый интегралвероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:

;

и т.д. Какой из этих функций пользоваться – вопрос вкуса. Мы выберем в качестве такой функции

. (6.3.5)

Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами .

Условимся называть функцию нормальной функцией распределения. В приложении (табл. 1) приведены таблицы значений функции .

Выразим функцию распределения (6.3.3) величины с параметрами и через нормальную функцию распределения . Очевидно,

. (6.3.6)

Теперь найдем вероятность попадания случайной величины на участок от до . Согласно формуле (6.3.1)

. (6.3.7)

Таким образом, мы выразили вероятность попадания на участок случайной величины , распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения , соответствующую простейшему нормальному закону с параметрами 0,1. Заметим, что аргументы функции в формуле (6.3.7) имеют очень простой смысл: есть расстояние от правого конца участка до центра рассеивания, выраженное в средних квадратических отклонениях; - такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания, и отрицательным, если слева.

Как и всякая функция распределения, функция обладает свойствами:

1. .

2. .

3. - неубывающая функция.

Кроме того, из симметричности нормального распределения с параметрами относительно начала координат следует, что

. (6.3.8)

Пользуясь этим свойством, собственно говоря, можно было бы ограничить таблицы функции только положительными значениями аргумента, но, чтобы избежать лишней операции (вычитание из единицы), в таблице 1 приложения приводятся значения как для положительных, так и для отрицательных аргументов.

Рис. 6.3.1.

На практике часто встречается задача вычисления вероятности попадания нормально распределеннойслучайной величины на участок, симметричный относительно центра рассеивания . Рассмотрим такой участок длины (рис. 6.3.1). Вычислим вероятность попадания на этот участок по формуле (6.3.7):

. (6.3.9)

Учитывая свойство (6.3.8) функции и придавая левой части формулы (6.3.9) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону на участок, симметричный относительно центра рассеивания:

. (6.3.10)

Решим следующую задачу. Отложим от центра рассеивания последовательные отрезки длиной (рис. 6.3.2) и вычислим вероятность попадания случайной величины в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону.

Рис. 6.3.2.

По формуле (6.3.7) находим:

(6.3.11)

Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т.д.) с точностью до 0,001 равны нулю.

Округляя вероятности попадания в отрезки до 0,01 (до 1%), получим три числа, которые легко запомнить:

0,34; 0,14; 0,02.

Сумма этих трех значений равна 0,5. Это значит, что для нормально распределенной случайной величины все рассеивания (с точностью до долей процента) укладывается на участке .

Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал её практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма». Из правила трех сигма вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения .

Пример 1. Случайная величина , распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния. При измерении допускается систематическая ошибка в сторону завышения на 1,2 (м); среднее квадратическое отклонения ошибки измерения равно 0,8 (м). Найти вероятность того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6 (м).

Решение. Ошибка измерения есть случайная величина , подчиненная нормальному закону с параметрами и . Нужно найти вероятность попадания этой величины на участок от до . По формуле (6.3.7) имеем:

Пользуясь таблицами функции (приложение, табл. 1), найдем:

; ,

откуда

Пример 2. Найти ту же вероятность, что и в предыдущем примере, но при условии, что систематической ошибки нет.

Решение. По формуле (6.3.10), полагая , найдем:

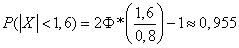Пример 3. По цели, имеющей вид полосы (автострада), ширина которой равна 20 м, ведется стрельба в направлении, перпендикулярном автостраде. Прицеливание ведется по средней линии автострады. Среднее квадратическое отклонение в направлении стрельбы равно м. Имеется систематическая ошибка в направлении стрельбы: недолет 3 м. Найти вероятность попадания в автостраду при одном выстреле.

Рис. 6.3.3.

Решение. Выберем начало координат в любой точке на средней линии автострады (рис. 6.3.3) и направим ось абсцисс перпендикулярно автостраде. Попадание или непопадание снаряда в автостраду определяется значением только одной координаты точки падения (другая координата нам безразлична). Случайная величина распределена по нормальному закону с параметрами , . Попадание снаряда в автостраду соответствует попаданию величины на участок от до . Применяя формулу (6.3.7), имеем:

Рис. 6.3.4.

Пример 4. Имеется случайная величина , нормально распределенная, с центром рассеивания (рис. 6.3.4) и некоторый участок оси абсцисс. Каково должно быть среднее квадратическое отклонение случайной величины для того, чтобы вероятность попадания на участок достигала максимума?