 |
Вероятное (срединное) отклонение
|
|
|
|
В ряде областей практических применений теории вероятностей (в частности, в теории стрельбы) часто, наряду со средним квадратическим отклонением, пользуются еще одной характеристикой рассеивания, так называемым вероятным, или срединным, отклонением. Вероятное отклонение обычно обозначается буквой 
(иногда В).
Вероятным (срединным) отклонением случайной величины 
, распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.
Геометрическая интерпретация вероятного отклонения показана на рис. 6.4.1. Вероятное отклонение – это половина длины участка оси абсцисс, симметричного относительно точки 
, на который опирается половина площади кривой распределения.
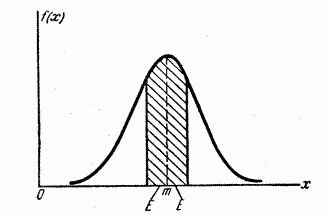
Рис. 6.4.1.
Поясним смысл термина «срединное отклонение» или «срединная ошибка», которым часто пользуются в артиллерийской практике вместо «вероятного отклонения».
Рассмотрим случайную величину , распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания меньше, чем на , по определению вероятного отклонения , равна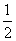 
:
. (6.4.1)
Вероятность того, что она отклонится от больше, чем на , тоже равна :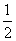
.
Таким образом, при большом числе опытов в среднем половина значений случайной величины отклонится от больше, чем на , а половина – меньше. Отсюда и термин «срединная ошибка», «срединное отклонение».
Очевидно, вероятное отклонение, как характеристика рассеивания, должно находиться в прямой зависимости от среднего квадратического отклонения 
. Вычислим вероятность события 
в уравнении (6.4.1) по формуле (6.3.10). Имеем:
.
Отсюда
|
|
|
. (6.4.2)
По таблицам функции 
можно найти такое значение аргумента 
, при котором она равна 0,75. Это значение приближенно равно 0,674; отсюда
; 
. (6.4.3)
Таким образом, зная значение , можно сразу найти пропорциональное ему значение . Часто пользуются еще такой формой записи этой зависимости:
, (6.4.4)
где 
- такое значение аргумента, при котором одна из форм интеграла вероятностей – так называемая функция Лапласа
- равна половине. Численное значение величины приближенно равно 0,477.
В настоящее время вероятное отклонение, как характеристика рассеивания, все больше вытесняется более универсальной характеристикой . В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.
Если в качестве характеристики рассеивания принято вероятное отклонение , то плотностьнормального распределения записывается в виде:
, (6.4.5)
а вероятность попадания на участок от 
до 
чаще всего записывается в виде:
, (6.4.6)
где
(6.4.7)
- так называемая приведенная функция Лапласа.
Сделаем подсчет, аналогичный выполненному в предыдущем n° для среднего квадратического отклонения : отложим от центра рассеивания последовательные отрезки длиной в одно вероятное отклонение (рис. 6.4.2) и подсчитаем вероятности попадания в эти отрезки с точностью до 0,01. Получим:
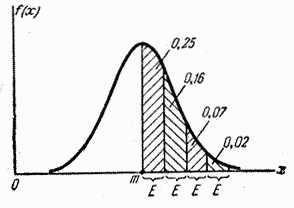
Рис. 6.4.2.
Отсюда видно, что с точностью до 0,01 все значения нормально распределенной случайной величиныукладываются на участке 
.
Пример. Самолет-штурмовик производит обстрел колонны войск противника, ширина которой равна 8 м. Полет – вдоль колонны; вследствие скольжения имеется систематическая ошибка: 2 м вправо по направлению полета. Главные вероятные отклонения: по направлению полета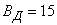 
м, в боковом направлении 
м. Не имея в своем распоряжении никаких таблиц интегралов вероятностей, а зная только числа:
25%, 16%, 7%, 2%,
оценить грубо-приближенно вероятность попадания в колонну при одном выстреле и вероятность хотя бы одного попадания при трех независимых выстрелах.
|
|
|
Решение. Для решения задачи достаточно рассмотреть одну координату точки попадания – абсциссу в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания 
и вероятным отклонением 
(м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:
.
Влево от центра рассеивания цель занимает участок 6 м. Это – целое вероятное отклонение (5 м), вероятность попадания в которое равна 25% плюс часть длиной 1 м следующего (второго от центра) вероятного отклонения, вероятность попадания в которое равна 16%. Вероятность попадания в часть длиной 1 м приближенно равна:
.
Таким образом, вероятность попадания в колонну приближенно равна:
.
Вероятность хотя бы одного попадания при трех выстрелах равна:
.
|
|
|
