 |
Нормальный закон на плоскости
|
|
|
|
Из законов распределения системы двух случайных величин имеет смысл специально рассмотреть нормальный закон, как имеющий наибольшее распространение на практике. Так как система двух случайных величин изображается случайной точкой на плоскости, нормальный закон для системы двух величин часто называют «нормальным» законом на плоскости.
В общем случае плотность нормального распределения двух случайных величин выражается формулой
. (9.1.1)
Этот закон зависит от пяти параметров: 
и 
. Смысл этих параметров нетрудно установить. Докажем, что параметры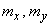 
представляют собой математические ожидания (центры рассеивания) величин 
и 
; 
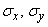— их средние квадратические отклонения; — коэффициент корреляции величин и .
Для того чтобы убедиться в этом, найдем прежде всего плотность распределения для каждой из величин, входящих в систему. Согласно формуле (8.4.2)
.
Вычислим интеграл
.
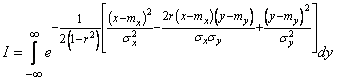Положим:
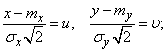(9.1.2)
тогда
.
Из интегрального исчисления известно, что
. (9.1.3)
В нашем случае
.
Подставляя эти значения в формулу (9.1.3), имеем:
,
откуда
,
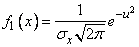или, учитывая (9.1.2)
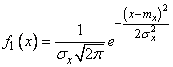. (9.1.4)
Таким образом, величина подчинена нормальному закону с центром рассеивания 
и средним квадратическим отклонением 
. Аналогично покажем, что
, (9.1.5)
т.е. величина подчинена нормальному закону с центром рассеивания 
и средним квадратическим отклонением 
.
Остается доказать, что параметр в формуле (9.1.1) представляет собой коэффициент корреляции величин и . Для этого вычислим корреляционный момент:
,
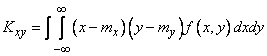где 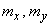- математические ожидания величин и .
Подставляя в эту формулу выражение 
, получим:
, (9.1.6)
где
.
Произведем в двойном интеграле (9.1.6) замену переменных, положив:
. (9.1.7)
Якобиан преобразования равен
|
|
|
,
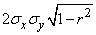следовательно,
Учитывая, что
имеем:
(9.1.8)
Таким образом, доказано, что параметр в формуле (9.1.1) представляет собой коэффициент корреляции величин и .
Предположим теперь, что случайные величины и , подчиненные нормальному закону на плоскости, не коррелированы; положим в формуле (9.1.1) 
. Получим:
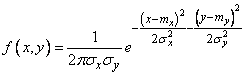. (9.1.9)
Легко убедиться, что случайные величины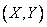 
, подчиненные закону распределения с плотностью (9.1.9), не только не коррелированы, но и независимы. Действительно.
.
т.е. плотность распределения системы равна произведению плотностей распределения отдельных величин, входящих в систему, а это значит, что случайные величины 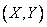независимы.
Таким образом, для системы случайных величин, подчиненных нормальному закону, из некоррелированности величин вытекает также их независимость. Термины «некоррелированные» и «независимые» величины для случаянормального распределения эквивалентны.
При 
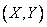случайные величины зависимы. Нетрудно убедиться, вычисляя условные законы распределенияпо формулам (8.4.6), что
Проанализируем один из этих условных законов распределения, например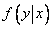 
. Для этого преобразуем выражение плотности 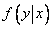к виду:
.
Очевидно, это есть плотность нормального закона с центром рассеивания
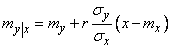(9.1.10)
и средним квадратическим отклонением
. (9.1.11)
Формулы (9.1.10) и (9.1.11) показывают, что в условном законе распределения величины при фиксированном значении 
от этого значения зависит только математическое ожидание, но не дисперсия.
Величина 
называется условным математическим ожиданием величины при данном 
. Зависимость (9.1.10) можно изобразить на плоскости 
, откладывая условное математическое ожидание по оси ординат. Получится прямая, которая называется линией регрессии на . Аналогично прямая
(9.1.12)
есть линия регрессии на .
Линии регрессии совпадают только при наличии линейной функциональной зависимости от . При независимых и линии регрессии параллельны координатным осям.
|
|
|
Рассматривая выражение (9.1.1) для плотности нормального распределения на плоскости, мы видим, что нормальный закон на плоскости полностью определяется заданием пяти параметров: двух координат центра рассеивания 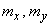, двух средних квадратических отклонений 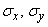и одного коэффициента корреляции . В свою очередь последние три параметра 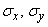и полностью определяются элементами корреляционной матрицы: дисперсиями 
и корреляционным моментом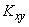 
. Таким образом, минимальное количество числовых характеристик системы – математические ожидания, дисперсии и корреляционный момент – в случае, когда система подчинения нормальному закону, определяет собой полностью закон распределения, т.е. образует исчерпывающую систему характеристик.
Так как на практике нормальный закон весьма распространен, то очень часто для полной характеристики закона распределения системы оказывается достаточно задать минимальное число – всего пять – числовых характеристик.
|
|
|
