 |
Эллипсы рассеивания. Приведение нормального закона к каноническому виду
|
|
|
|
Рассмотрим поверхность распределения, изображающую функцию (9.1.1). Она имеет вид холма, вершина которого находится над точкой 
(рис. 9.2.1).
В сечении поверхности распределения плоскостями, параллельными оси 
, получаются кривые, подобные нормальным кривым распределения. В сечении поверхности распределения плоскостями, параллельными плоскости 
, получаются эллипсы. Напишем уравнение проекции такого эллипса на плоскость :
,
или, обозначая константу 
,
. (9.2.1)
Уравнение эллипса (9.2.1) можно проанализировать обычными методами аналитической геометрии. Применяя их, убеждаемся, что центр эллипса (9.2.1) находится в точке с координатами ; что касается направления осей симметрии эллипса, то они составляют с осью 
углы, определяемые уравнением
. (9.2.2)
Рис. 9.2.1
Это уравнение дает два значения углов: 
и 
, различающиеся на 
.
Таким образом, ориентация эллипса (9.2.1) относительно координатных осей находится в прямой зависимости откоэффициента корреляции 
системы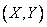 
; если величины не коррелированны (т.е. в данном случае и независимы), то оси симметрии эллипса параллельны координатным осям; в противном случае они составляют с координатными осями некоторый угол.
Пересекая поверхность распределения плоскостями, параллельными плоскости , и проектируя сечения на плоскость мы получим целое семейство подобных и одинаково расположенных эллипсов с общим центром . Во всех точках каждого из таких эллипсов плотность распределения постоянна. Поэтому такие эллипсы называются эллипсами равной плотности или, короче эллипсами рассеивания. Общие оси всех эллипсов рассеивания называются главными осями рассеивания.
Известно, что уравнение эллипса принимает наиболее простой, так называемый «канонический» вид, если координатные оси совпадают с осями симметрии эллипса. Для того чтобы привести уравнение эллипса рассеивания к каноническому виду, достаточно перенести начало координат в точку и повернуть координатные оси на угол , определяемый уравнением (9.2.2). При этом координатные оси совпадают с главными осями рассеивания, инормальный закон на плоскости преобразуется к так называемому «каноническому» виду.
|
|
|
Каноническая форма нормального закона на плоскости имеет вид
, (9.2.3)
где 
— так называемые главные средние квадратические отклонения, т.е. средние квадрадитеские отклонения случайных величин 
, представляющих собой координаты случайной точки в системе координат, определяемой главными осями рассеивания 
. Главные средние квадратичские отклонения 
и 
выражаются через средние квадратические отклонения в прежней системе координат формулами:
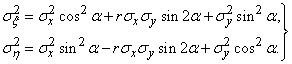(9.2.4)
Обычно, рассматривая нормальный закон на плоскости, стараются заранее выбрать координатные оси 
так, чтобы они совпали с главными осями рассеивания. При этом средние квадратические отклонения по осям 
и будут главными средними квадратическими отклонениями, и нормальный закон будет иметь вид:
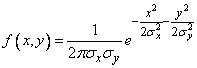. (9.2.5)
В некоторых случаях координатные оси выбирают параллельно главным осям рассеивания, но начало координат с центром рассеивания не совмещают. При этом случайные величины 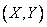также оказываются независимыми, но выражение нормального закона имеет вид:
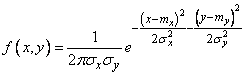, (9.2.6)
где 
и 
— координаты центра рассеивания.
Перейдем в канонической форме нормального закона (9.2.5) от средних квадратических отклонений квероятным отклонениям:
.
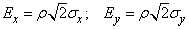Величины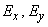 
называются главными вероятными отклонениями. Подставляя выражения 
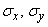через 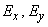в уравнение (9.2.5), получим другую каноническую форму нормального закона:
. (9.2.7)
В такой форме нормальный закон часто применяется в теории стрельбы.
|
|
|
Напишем уравнение эллипса рассеивания в каноническом виде:
или 
. (9.2.8)
где 
- постоянное число.
Из уравнения видно, что полуоси эллипса рассеивания пропорциональны главным средним квадратическим отклонениям (а значит, и главным вероятным отклонениям).
Назовем «единичным» эллипсом рассеивания тот из эллипсов равной плотности вероятности, полуоси которого равны главным средним квадратическим отклонениям 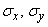. (Если пользоваться в качестве характеристик рассеивания не главными средними квадратическими, а главными вероятными отклонениями, то естественно будет назвать «единичным» тот эллипс, полуоси которого равны ).
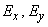Кроме единичного эллипса рассеивания иногда рассматривают еще «полный» эллипс рассеивания, под которым понимают тот из эллипсов равной плотности вероятности, в который с практической достоверностью укладывается все рассеивание. Размеры этого эллипса, разумеется, зависят от того, что понимать под «практической достоверностью». В частности, если принять за «практическую достоверность» вероятность порядка 
, то «полным эллипсом рассеивания» можно считать эллипс с полуосями 
.
Рассмотрим специально один частный случай, когда главные средние квадратические отклонения равны друг другу:
.
Тогда все эллипсы рассеивания обращаются в круги, и рассеивание называется круговым. При круговом рассеивании каждая из осей, проходящих через центр рассеивания, может быть принята за главную ось рассеивания, или, другими словами, направление главных осей рассеивания неопределенно. При некруговом рассеивании случайные величины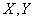 
, подчиненные нормальному закону на плоскости, независимы тогда и только тогда, когда координатные оси параллельны главным осям рассеивания; при круговом рассеивании случайные величины 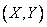независимы при любом выборе прямоугольной системы координат. Эта особенность кругового рассеивания приводит к тому, что оперировать с круговым рассеиванием гораздо удобнее, чем с эллиптическим. Поэтому на практике, где только возможно, стремятся приближенно заменять некруговое рассеивание круговым.
|
|
|
