 |
Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии
|
|
|
|
В предыдущем 
мы рассмотрели полную (или среднюю) информацию о системе 
, содержащуюся в сообщении о том, в каком состоянии находится система 
. В ряде случаев представляет интерес оценить частную информацию о системе , содержащуюся в отдельном сообщении, указывающем, что система находится в конкретном состоянии 
. Обозначим эту частную информацию 
. Заметим, что полная (или, иначе, средняя) информация 
должна представлять собой математическое ожидание частной информации для всех возможных состояний, о которых может быть передано сообщение:
. (18.6.1)
Придадим формуле (18.5.14), по которой вычисляется (она же 
), такой вид, как у формулы (18.6.1):
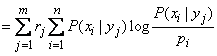, (18.6.2)
откуда, сравнивая с формулой (18.6.1), получим выражение частной информации:
. (18.6.3)
Выражение (18.6.3) и примем за определение частной информации. Проанализируем структуру этого выражения. Оно представляет собой не что иное, как осредненное по всем состояниям 
значение величины
. (18.6.4)
Осреднение происходит с учетом различных вероятностей значений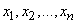 
. Так как система уже приняла состояние , то при осреднении значения (18.6.4) множатся не на вероятности 
состояний , а на условные вероятности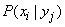 
.
Таким образом, выражение для частной информации можно записать в виде условного математического ожидания:
. (18.6.5)
Докажем, что частная информация , так же как и полная, не может быть отрицательна. Действительно, обозначим:
(18.6.6)
и рассмотрим выражение
.
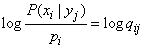Легко убедиться (см. рис. 18.6.1), что при любом 
. (18.6.7)
Рис. 18.6.1.
Полагая в (18.6.7) 
, получим:
; 
,
откуда
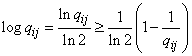. (18.6.8)
На основании (18.6.3) и (18.6.6) имеем:
.
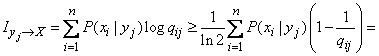
Но
,
и выражение в фигурной скобке равно нулю; следовательно 
.
Таким образом, мы доказали, что частная информация о системе , заключенная в сообщении о любом состоянии системы , не может быть отрицательной. Отсюда следует, что неотрицательна и полная взаимная информация (как математическое ожидание неотрицательной,случайной величины):
|
|
|
. (18.6.9)
Из формулы (18.5.6) для информации: 
следует, что
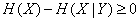(18.6.10)
или
,
т. е. полная условная энтропия системы не превосходит ее безусловной энтропии.
Таким образом, доказано положение, принятое нами на веру в 18.3.
Для непосредственного вычисления частной информации формулу (18.6.3) удобно несколько преобразовать, введя в нее вместо условных вероятностей 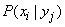безусловные. Действительно,
,
и формула (18.6.3) принимает вид
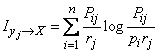. (18.6.11)
Пример 1. Система 
характеризуется таблицей вероятностей 
:
|
| 
| 
| 
|
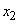
| 0,1 | 0,2 | 0,3 |
| 0,3 | 0,4 | 0,7 |
|
| 0,4 | 0,6 |
Найти частную информацию о системе , заключенную в сообщении 
.
Решение. По формуле (18.6.11) имеем:
.
По таблице 6 приложения находим
,
,
(дв. ед.).
Мы определили частную информацию о системе , содержащуюся в конкретном событии 
, т. е. в сообщении «система находится в состоянии ». Возникает естественный вопрос: а нельзя ли пойти еще дальше и определить частную информацию о событии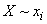 
, содержащуюся в событии 
? Оказывается, это можно сделать, только получаемая таким образом информация «от события к событию» будет обладать несколько неожиданными свойствами: она может быть как положительной, так и отрицательной.
Исходя из структуры формулы (18.6.3), естественно определить информацию «от события к событию» следующим образом:
, (18.6.12)
т. е. частная информация о событии, получаемая в результате сообщения о другом событии, равна логарифму отношения вероятности первого события после сообщения к его же вероятности до сообщения (априори).
Из формулы (18.6.12) видно, что если вероятность события 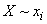в результате сообщения увеличивается, т. е.
,
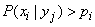то информация 
положительна; в противном случае она отрицательна. В частности, когда появление события полностью исключает возможность появления события 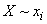(т. е. когда эти события несовместны), то
|
|
|
Информацию можно записать в виде:
, (18.6.13)
из чего следует, что она симметрична относительно и , и
. (18.6.14)
Таким образом, нами введены три вида информации:
1) полная информация о системе , содержащаяся в системе :
;
2) частная информация о системе , содержащаяся в событии (сообщении) :
3) частная информация о событии 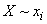, содержащаяся в событии (сообщении) :
.
Первые два типа информации неотрицательны; последняя может быть как положительной, так и отрицательной.
Пример 2. В урне 3 белых и 4 черных шара. Из урны вынуто 4 шара, три из них оказались черными, а один - белым. Определить информацию заключенную в наблюденном событии 
по отношению к событию 
- следующий вынутый из урны шар будет черным.
Решение.
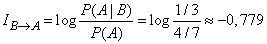(дв. ед.).
|
|
|
