Передача информации с искажениями. Пропускная способность канала с помехами

В предыдущем мы рассмотрели вопросы, связанные с кодированием и передачей информации по каналу связи в идеальном случае, когда процесс передачи информации осуществляется без ошибок. В действительности этот процесс неизбежно сопровождается ошибками (искажениями). Канал передачи, в котором возможны искажения, называется каналом с помехами (или шумами). В частном случае ошибки возникают в процессе самого кодирования, и тогда кодирующее устройство может рассматриваться как канал с помехами.

Совершенно очевидно, что наличие помех приводит к потере информации. Чтобы в условиях наличия помех получить на приемнике требуемый объем информации, необходимо принимать специальные меры. Одной из таких мер является введение так называемой «избыточности» в передаваемые сообщения; при этом источник информации выдает заведомо больше символов, чем это было бы нужно при отсутствии помех. Одна из форм введения избыточности - простое повторение сообщения. Таким приемом пользуются, например, при плохой слышимости по телефону, повторяя каждое сообщение дважды. Другой общеизвестный способ повышения надежности передачи состоит в передаче слова «по буквам» - когда вместо каждой буквы передается хорошо знакомое слово (имя), начинающееся с этой буквы.

Заметим, что все живые языки естественно обладают некоторой избыточностью. Эта избыточность часто помогает восстановить правильный текст «по смыслу» сообщения. Вот почему встречающиеся вообще нередко искажения отдельных букв телеграмм довольно редко приводят к действительной потере информации: обычно удается исправить искаженное слово, пользуясь одними только свойствами языка. Этого не было бы при отсутствии избыточности. Мерой избыточности языка служит величина

, (18.9.1)

где - средняя фактическая энтропия, приходящаяся на один передаваемый символ (букву), рассчитанная для достаточно длинных отрывков текста, с учетом зависимости между символами, - число применяемых символов (букв), - максимально возможная в данных условиях энтропия на один передаваемый символ, которая была бы, если бы все символы были равновероятны и независимы.

Расчеты, проведенные на материале наиболее распространенных европейских языков, показывают, что их избыточность достигает 50% и более (т. е., грубо говоря, 50% передаваемых символов являются лишними и могли бы не передаваться, если бы не опасность искажений).

Однако для безошибочной передачи сведений естественная избыточность языка может оказаться как чрезмерной, так и недостаточной: все зависит от того, как велика опасность искажений («уровень помех») в канале связи.

С помощью методов теории информации можно для каждого уровня помех найти нужную степень избыточности источника информации. Те же методы помогают разрабатывать специальные помехоустойчивые коды (в частности, так называемые «самокорректирующиеся» коды). Для решения этих задач нужно уметь учитывать потерю информации в канале, связанную с наличием помех.

Рассмотрим сложную систему, состоящую из источника информации , канала связи 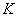и приемника (рис. 18.9.1).

Рис. 18.9.1.

Источник информации представляет собой физическую систему , которая имеет возможных состояний

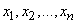
с вероятностями

.

Будем рассматривать эти состояния как элементарные символы, которые может передавать источник через канал 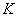к приемнику . Количество информации на один символ, которое дает источник, будет равно энтропии на один символ:

.

Если бы передача сообщений не сопровождалась ошибками, то количество информации, содержащееся в системе относительно , было бы равно самой энтропии системы . При наличии ошибок оно будет меньше:

.

Естественно рассматривать условную энтропию как потерю информации на один элементарный символ, связанную с наличием помех.

Умея определять потерю информации в канале, приходящуюся на один элементарный символ, переданный источником информации, можно определить пропускную способность канала с помехами, т. е. максимальноеколичество информации, которое способен передать канал в единицу времени.

Предположим, что канал может передавать в единицу времени элементарных символов. В отсутствие помехпропускная способность канала была бы равна

, (18.9.2)

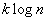так как максимальное количество информации, которое может содержать один символ, равно , а максимальное количество информации, которое могут содержать символов, равно , и оно достигается, когда символы появляются независимо друг от друга.

Теперь рассмотрим канал с помехами. Его пропускная способность определится как

, (18.9.3)

где - максимальная информация на один символ, которую может передать канал при наличии помех.

Определение этой максимальной информации в общем случае - дело довольно сложное, так как она зависит от того, как и с какими вероятностями искажаются символы; происходит ли их перепутывание, или же простое выпадение некоторых символов; происходят ли искажения символов независимо друг от друга и т. д.

Однако для простейших случаев пропускную способность канала удается сравнительно легко рассчитать.

Рассмотрим, например, такую задачу. Канал связи 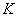передает от источника информации к приемнику элементарные символы 0 и 1 в количестве символов в единицу времени. В процессе передачи каждый символ, независимо от других, с вероятностью может быть искажен (т. е. заменен противоположным). Требуется найти пропускную способность канала.

Определим сначала максимальную информацию на один символ, которую может передавать канал. Пусть источник производит символы 0 и 1 с вероятностями и .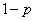

Тогда энтропия источника будет

.

Определим информацию на один элементарный символ:

.

Чтобы найти полную условную энтропию , найдем сначала частные условные энтропии: (энтропию системы при условии, что система приняла состояние ) и (энтропию системы при условии, что система приняла состояние 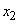). Вычислим , для этого предположим, что передан элементарный символ 0. Найдем условные вероятности того, что при этом система находится в состоянии и в состоянии 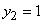. Первая из них равна вероятности того, что сигнал не перепутан:

;

вторая - вероятности того, что сигнал перепутан:

.

Условная энтропия будет:

.

Найдем теперь условную энтропию системы при условии, что (передан сигнал единица):

; ,

откуда

.

Таким образом,

. (18.9.4)

Полная условная энтропия получится, если осреднить условные энтропии и с учетомвероятностей и 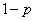значений . Так как частные условные энтропии равны, то

.

Мы получили следующий вывод: условная энтропия совсем не зависит от того, с какими вероятностями встречаются символы 0; 1 в передаваемом сообщении, а зависит только от вероятности ошибки .

Вычислим полную информацию, передаваемую одним символом:

,

где - вероятность того, что на выходе появится символ 0. Очевидно, при заданных свойствах канала информация на один символ достигает максимума, когда максимально. Мы знаем, что такая функция достигает максимума при , т. е. когда на приемнике оба сигнала равновероятны. Легко убедиться, что это достигается, когда источник передает оба символа с одинаковой вероятностью . При том же значении достигает максимума и информация на один символ. Максимальное значение равно

.

Следовательно, в нашем случае

,

и пропускная способность канала связи будет равна

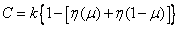. (18.9.5)

Заметим, что 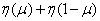есть не что иное, как энтропия системы, имеющей два возможных состояния с вероятностями и . Она характеризует потерю информации на один символ, связанную с наличием помех в канале.

Пример. 1. Определить пропускную способность канала связи, способного передавать 100 символов 0 или 1 в единицу времени, причем каждый из символов искажается (заменяется противоположным) с вероятностью .

Решение. По таблице 7 приложения находим

,

,

.

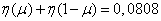На один символ теряется информация 0,0808 (дв. ед). Пропускная способность канала равна

двоичные единицы в единицу времени.

С помощью аналогичных расчетов может быть определена пропускная способность канала и в более сложных случаях: когда число элементарных символов более двух и когда искажения отдельных символов зависимы. Знаяпропускную способность канала, можно определить верхний предел скорости передачи информации по каналу с помехами. Сформулируем (без доказательства) относящуюся к этому случаю вторую теорему Шеннона.

 

Я теорема Шеннона

Пусть имеется источник информации , энтропия которого в единицу времени равна , и канал с пропускной способностью . Тогда если

,

то при любом кодировании передача сообщений без задержек и искажений невозможна. Если же

,

то всегда можно достаточно длинное сообщение закодировать так, чтобы оно было передано без задержек и искажений с вероятностью, сколь угодно близкой к единице.

Пример 2. Имеются источник информации с энтропией в единицу времени (дв. ед.) и два канала связи; каждый из них может передавать в единицу времени 70 двоичных знаков (0 или 1); каждый двоичный знак заменяется противоположным с вероятностью . Требуется выяснить: достаточна ли пропускная способность этих каналов для передачи информации, поставляемой источником?

Решение. Определяем потерю информации на один символ:

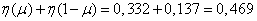(дв. ед.).

Максимальное количество информации, передаваемое по одному каналу в единицу времени:

.

Максимальное количество информации, которое может быть передано по двум каналам в единицу времени:

(дв. ед.),

чего недостаточно для обеспечения передачи информации от источника.

 

⇐ Предыдущая76777879808182838485Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: