 |
Численное решение дифференциальных уравнений
|
|
|
|
Численными методами решается уравнение первого порядка в виде: y' = f(x,y) с заданными начальными условиями x0, y0, где x и y - независимая (обычно время) и зависимая переменные. В дальнейшем будем считать такое уравнение записанным в стандартном виде.
Уравнения высших порядков приводят к системе уравнений первого порядка введением дополнительных переменных. Например, для уравнения второго порядка
y" = f(x,y',y)
примем v= y'. Тогда y" = v' и имеем систему уравнений:
v’ = f(x, y, v);
y’ = v.
Графическая интерпретация численного решения обыкновенного дифференциального уравнения показана на рис. 7 на примере простейшего метода Эйлера. Известной является функция y0 в точке x0.

Рис. 7. Графическая интерпретация метода Эйлера
Решение находится для ряда значений независимой переменной х с шагом h:
x1 = x0 + h; x2 = x1 + h;... xn+1 = xn + h.
Значение y1 (рис. 7) находится на пересечении прямой, проведенной из точки (х0,у0) под углом a0 = arctg(y0') и перпендикуляра, проведенного к оси абсцисс из точки х1. Процесс последовательно повторяется для других значений х:
y1 = y0 + h×y0' = y0 + h×f(x0,y0),
y2 = y1 + h×y1' = y1 + h×f(x1,y1),...
yn+1 = yn + h×yn' = yn + h×f(xn,yn).
Недостатком данного метода является низкая точность решения. Для повышения точности решения уменьшают шаг счета h или используют методы более высокого порядка. Под порядком метода понимается максимальный порядок производной ряда Тейлора, учитываемый в численном методе
|
|
|
yn+1 = yn + h·yn' +h2/2·y” +h3/6·y(3) +...
Метод Эйлера учитывает производную только первого порядка, поэтому является методом первого порядка. Чаще всего используется метод Рунге-Кутта четвертого порядка, алгоритм которого имеет вид:
yn+1 = yn + (k1 + 2×k2 +2×k3 + k4) / 6,
где k1 = h×f(xn,yn);
k2 = h×f(xn + 0.5×h,yn + 0.5×k1);
k3 = h×f(xn + 0.5×h,yn + 0.5×k2);
k4 = h×f(xn + h,yn + k3).
Начало программы (вариант) для решения дифференциального уравнения второго порядка
m×x" + b×x' + c×x = F
показано ниже.
Program DIFUR;
Uses Crt,Dos,Lib,Graph;
type mas = array[1..10] of real;
Var Rez :text; d,y,y1:mas;
Filerez,text,Sxmax,Sxst,Stmax :string[50];
m,b,c,F,h,hp,t,tp,tmax,xmax,xst,nx,ny,nmax:real;
n :integer;
KL,nd,j :byte;
Procedure Prav(var y,d:mas);
í y[1] = x' - скорость массы d[1] = x''- ускорение массы ý
í y[2] = x - перемещение массы d[2] = x' - скорость массы ý
begin
d[1]:= (F - b*y[1] - c*y[2])/m; d[2]:= y[1];
end;
Procedure Rynge;
Var j:byte; yy,k:array[1..nd] of real;
begin
Prav(y,d);
For j:=1 to nd do begin
yy[j]:=y[j]; k[j]:=h*d[j]; y1[j]:=yy[j] + 0.5*k[j]; y[j]:=y[j] + k[j]/6; end;
t:=t+0.5*h; Prav(y1,d);
For j:=1 to nd do begin
k[j]:=h*d[j]; y1[j]:=yy[j] + 0.5*k[j]; y[j]:=y[j] + k[j]/3; end;
Prav(y1,d);
For j:=1 to nd do begin
k[j]:=h*d[j]; y1[j]:=yy[j] + k[j]; y[j]:=y[j] + k[j]/3; end;
t:=t+0.5*h; Prav(y1,d);
For j:=1 to nd do begin k[j]:=h*d[j]; y[j]:=y[j] + k[j]/6; end;
end;
Procedure Start;...
Процедура Prav (var y,d:max) предназначена для вычисления правых частей уравнений. Использованные в ней массивы типа mas: y – вектор - решение (выходные параметры); d - производные вектор - решения (производные выходных параметров).
Процедура Rynge реализует метод Рунге-Кутта четвертого порядка.
Метод итераций
Метод итераций (метод последовательных приближений) предназначен для нахождения корней алгебраических и трансцендентных уравнений. Для этого исходное уравнение F(x) = 0 нужно преобразовать в эквивалентное x = f(x), например, добавлением в левую и правую части исходного уравнения F(x) = 0 переменной х.
|
|
|
Сначала задаются первоначальным значением x = x(0) и находят первое приближение:
x(1) = f[x(0)].
Аналогично находят следующие приближения:
x(2) = f[x(1)],..., x(i+1) = f[x(i)].
Расчет завершается, если достигается заданная точность е
|x(i+1) – x(i)| < е.
Процеcс сходящийся, если ú df/dxú < 1.
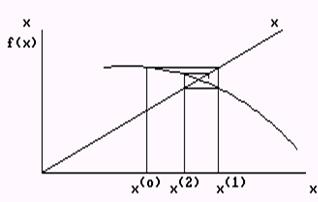
Графическая интерпретация метода итераций показана на рис. 8 а. Точное решение соответствует пересечению функции f(x) с осью абсцисс х.
Для уравнений типа
F(x) = a0×xn + a 1×xn-1 +... + an = 0
удобным в использовании является метод Ньютона (метод касательных), итерационная формула для которого имеет вид:
 , где F’(x) = dF/dx (рис.8 б).
, где F’(x) = dF/dx (рис.8 б).
 |  | ||
а) б)
Рис. 8. Графическая интерпретация методов итераций (а) и Ньютона (б)
Структурные схемы и графы
Представляют собой графическую запись уравнений и наглядно показывают связи между отдельными элементами объекта. Структурные схемы и графы можно по определенным правилам преобразовывать и упрощать. Такие действия эквивалентны алгебраическим преобразованиям систем уравнений. Они имеют геометрическую интерпретацию и уменьшают вероятность появления ошибок. По структурным схемам и графам записываются топологические формулы, которые впервые предложены Кирхгофом (1874 г.) и Максвеллом (1892 г.).
Структурные схемы и графы можно составлять по уравнениям и по геометрическому виду объекта. В последнем случае объект рассматривается состоящим из отдельных элементов, для каждого из которых имеются частные структурные схемы и графы.
Структурные схемы
В структурных схемах математические операции изображаются прямоугольником, внутри которого указывается вид операции (рис. 9).
|
|
|

Рис. 9. Примеры условных обозначений математических
операций на структурных схемах
В соответствии с рис. 9 один из вариантов структурной схемы для дифференциального уравнения
y” + a1y’ + a2y = F
 |
будет иметь следующий вид (рис.10):
Рис. 10. Структурная схема дифференциального уравнения
второго порядка (вариант)
Графы
Теория направленных графов получила основное развитие за рубежом. Разработано несколько типов графов, с помошью которых решаются системы линейных алгебраических уравнений. Наиболее известен М-граф, предложенный Мэзоном в 1956 г. Он представляет собой графическую трактовку известного в математике правила Крамера. Мэзон показал, что определитель системы имеет вполне определенный физический смысл и разработал упорядоченную методику его нахождения.
При использовании графов исходные уравнения заменяются графом. Затем по его виду записывается решение в виде передаточной функции (см. ниже). Граф, как и структурная схема строится по определенным правилам. Его вид зависит от геометрии объекта и принятых выходных координат.
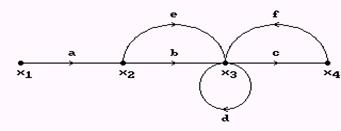 |
Графом называют геометрическую фигуру, образованную точками и соединяющими их линиями (рис. 11).
Рис. 11. Пример графа объекта
Точки х1, х2, х3 и х4 называют вершинами или узлами графа. Они соответствуют принятым входным и выходным координатам. Линии a, b, c, …f называют ветвями или ребрами графа. Они определяют связи и соотношения между координатами графа.
Направления передачи сигналов указывают стрелками. Ветви графа образуют пути прохождения сигналов. Различают прямые и обратные, замкнутые и разомкнутые пути. В замкнутом пути (на рис.12 путь f-a) сигнал возвращается к исходному узлу. Он образует контур обратной связи, частным случаем которого является петля (путь d).
|
|
|
Правила упрощения и преобразования графов.
Правило 1. Устранение узла. x2=ax1; x3=bx2=abx1

Правило 2. Объединение ветвей. х2=аx1+bx1=(a+b)x1

Правило 3. Устранение простой узловой точки.
x4=ax1; x2=bx4; x3=ax4; x2=abx1; x3=acx1

Правило 4. Устранение контура обратной связи на пути прохождения сигнала.
x2=ax1+cx3; x3=bx2; x3=abx1+bcx

Правило 5. Исключение петли.
x2=ax1+cx2; x2=a/(1-c)x1; x3=bx2; x3=ab/(1-c)x1

Пример. Построить граф для трехмассовой динамической модели (рис. 12)
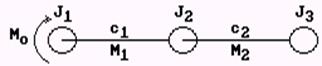
Рис.12. Трехмассовая динамическая модель
Примем в качестве выходных координат скорости масс и моменты в упругих звеньях. Уравнения движения для рассматриваемой модели
J1j1”+M1=M0;
J2j2”-M1+M2=0;
J3j3”-M2=0,
где M1=c1(j1-j2); M2=c2(j2-j3).
Запишем их в виде
j1’= 1/(J1s)M0 – 1/(J1s)M1;
j2’= 1/(J2s)M1 – 1/(J2s)M2;
j3’= 1(J3s)M2,
где 1/s – символ интегрирования. Соответствующий граф показан на рис. 13.

Рис.13. Вариант графа трехмассовой динамической модели
|
|
|


