Амплитудные частотные характеристики

Амплитудная частотная характеристика представляет собой отношение амплитуды выходного установившегося сигнала к амплитуде входного гармонического воздействия различной частоты.

АЧХ можно найти из КЧХ, разложив последнюю на вещественную ReW и мнимую ImW части:

                                           W(jw) = ReW + jImW,   где j = .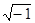

Тогда АЧХ будет равна

                                           A(w) = .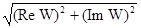

Пример. Найти АЧХ для объекта, поведение которого описывается уравнением

                                            a₀y”+a₁y’+a₂y=bx,

Решение. Передаточная функция равна

                                           W(s)=

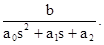
После замены s на jw получаем

                                           W(jw) =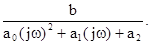

Разделив последнее выражение на вещественную и мнимую части, после простых преобразований находим АЧХ

                                             A(w) =

Более просто АЧХ находится при использовании выражения

                                             A(w) =  .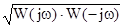

Типичный график АЧХ показан на рис. 15.

                       

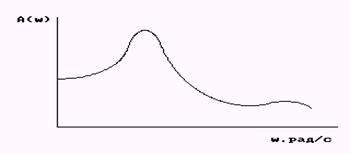
      Рис. 15. Пример графика амплитудной частотной характеристики объекта.

 

Точки максимумов АЧХ соответствуют резонансным частотам объекта. При уменьшении трения в системе эти максимумы увеличиваются, стремясь к бесконечности при уменьшении трения до нуля.

Собственные колебания и формы

Собственными называют периодические колебания консервативной систе­мы, совершающиеся исключительно под воздействием инерционных и упругих сил. Для возбуждения таких колебаний достаточно приложить к системе какое-нибудь начальное возмущение, т. е. вывести ее из состояния равновесия. После прекращения действия возмущения в системе устанавливаются собственные колебания. Углы поворота масс описываются уравнением (например, рис.14 а)

                                                  j_i = åA_ij sin(w_jt + a_j),

где i – номер  массы, j – порядковый номер собственной частоты,  a_j – фазовый угол, Aij – амплитуда колебаний i – ой массы на j – ой собственной частоте.

Из формулы следует, что в общем случае все массы системы совершают сложное колебательное движение, называемое полигармоническим. Можно выбрать такие начальные возмущения, при которых все массы будут совершать гармонические колебания с некоторой одной частотой w_j, но с разными амплитудами. Эти колебания называют главными или нормальными колебаниями: 

                                                   j_ij = A_ij sin(w_jt + a_j).

Одинаковый фазовый угол a_j  означает, что массы системы одновременно проходят через положение равновесия и одновременно достигают максимальных значений. Совокупность амплитуд называют формой колебаний. У каждой собственной частоты имеется своя форма колебаний, называемая главной. Число форм колебаний равно числу собственных частот системы. В теории колебаний доказывается, что энергия одной формы колебаний не может переходить в энергию колебаний другой формы.

Линия, соединяющая концы амплитуд, называется упругой линией (рис. 16). Ее пересечение с осью абсцисс представляет собой узел колебаний. Число узлов равно номеру собственной частоты. В узле колебаний сечение вала не перемещается. Тангенс угла наклона упругой линии пропорционален моменту в упругом звене.

 

        

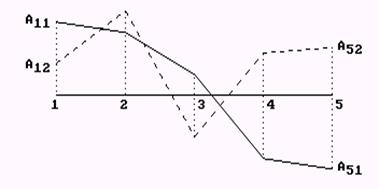
Рис. 16. Формы колебаний пятимассовой динамической модели (рис. 12 а):

¾¾ первая форма; ------ вторая форма

 

Собственные частоты

 

Для нахождения собственных частот W_i нужно в каком-либо виде записать частотное уравнение R(w) как функцию инерционных и упругих параметров модели. Корни этого уравнения являются собственными частотами колебаний. Собственные частоты нумеруют в порядке возрастания, начиная с W₁,

График изменения R(w) показан рис 17. Точки пересе­чения R(w) с осью абсцисс соответствуют собственным частотам. Критерием нахождения собственной частоты в интервале w_i... w_i+1 является знак произведения

                                                z = R(w_i)×R(w_i+1) £0,

который должен быть отрицательным или равным нулю.

Используя линейную интерполяцию, находим j-ю собственную частоту модели:

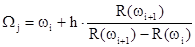                                   , где h – шаг расчета.

   

               Рис. 17. График изменения частотной функции R(v).

 

Число собственных частот, отличных от нуля, равно числу упругих звеньев модели. Таким образом, для нахождения собственных частот сначала надо записать частотное уравнение и, увеличивая w от w_min (обычно w_min = 0), найти нужное количество пересечений функции R(w) с частотной осью w.

Для записи частотного уравнения используют разные методы.

В общем виде для рассчитываемой консервативной мо­дели составляются уравнения движения, которые затем записываются в преобразованиях Лапласа. Полученную систему алгебраических уравнений записывают в систематизированном виде и составляют характеристический определитель. Затем его преобразовывают в частотный определитель R(w) заменой оператора s на jw (или s² на –w²). Таким образом, получают час­тотное уравнение в виде определителя. Например, для модели с четырьмя парциальными системами:

                        ,

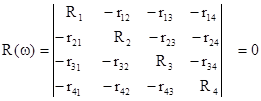где R_i = l_i - w_i, i = 1,4 - частотные уравнения парциальных систем;

l_i- квадраты собственных частот парциальных систем;

r_i,i+1 - коэффициенты связи одной парциальной системы с другой.

Описанный выше метод нахождения частотного уравнения известен в литературе как матричный метод.

Частотное уравнение динамической модели достаточно просто за­писывается с помощью последовательного расщепления на отдельные части (подсистемы). Такой метод известен как метод последовательного расщепления. Он является логическим развитием матричного метода.

Система сначала делится на две подсистемы с повторением какой-нибудь массы J_к. Частотное уравнение всей системы равно произведению частотных уравнений этих подсистем минус произведение коэффици­ента связи g_к-1,к  между ними, умноженное на частотные уравнения подсистем, которые получаются из исходной, если отбросить массу J_к и разорвать упругие звенья c_к-1 и c_к. Аналогичным методом выполняется дальнейшее расщепление системы. Если расщепление выполняется на массе, которая связана с нес­колькими упругими звеньями, то необходимо учитывать все возможные пути прохождения сигналов из одной подсистемы в другую.

На рис. 18 процесс последовательного расщепления показан на примере 5-массовой динамической модели.

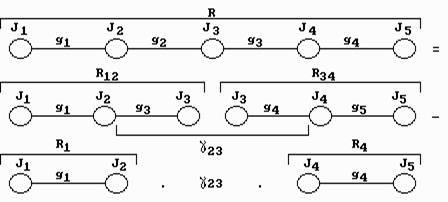
          Рис.18. Графическая интерпретация последовательного расщепления

                                                     динамической модели

 

В качестве примера на рис. 19 приведены частотные уравнения динамических моделей, показанных на рис. 14. Нижние индексы соответствуют номерам упругих звеньев, верхние - номерам неподвижно закрепленных масс.

После несложных преобразований частотное уравнение можно записать в виде алгебраического полинома:

                              ,

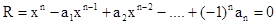где x = w² ; n - количество упругих звеньев.

В соответствии с формулами Виета, устанавливающими связь между коэффициентами уравнения и его корнями

   a₁ = x₁ + x₂ +... + x_n; a₂ = x ₁x₂ + x ₁x₃ +... + x _n-1x_n;..... a_n = x ₁x ₂x₃...x_n .

 

                                                                    а)

     

                                                                    б)

      

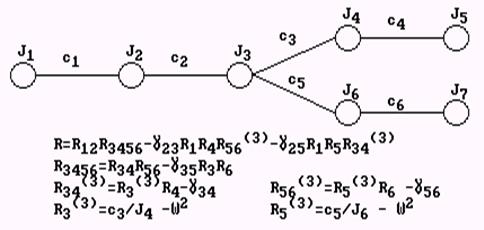
                                                                    в)

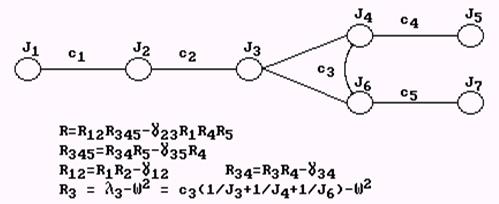
    Рис. 19. Частотные уравнения динамических моделей различных типов

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: