 |
Передаточные функции объектов
|
|
|
|
Нахождение передаточной функции в общем случае сводится к составлению уравнений движения, записи их в преобразованиях Лапласа и решении относительно изображений обобщенных координат – выходной и входной. Под передаточной функцией понимают отношение изображения выходной координаты к изображению входной координаты при нулевых начальных условиях. Рассмотрим сказанное на простом примере. Пусть поведение объекта описывается дифференциальным уравнением
a0y”+a1y’+a2y=b0x’+b1x,
где y и x – соответственно выходная и входная координаты.
Преобразованное по Лапласу дифференциальное уравнение имеет вид:
(a0s2+a1s+a2)y(s)=(b0 s+b1)x(s).
Отсюда передаточная функция равна W(s)= 
Для системы уравнений используют правило Крамера.
Пример. Для трехмассовой динамической модели (рис. 12) найти передаточные функции W1(s)= 
и W2(s)= между моментами М1 и М2 в упругих звеньях и входным моментом М0.
Решение. Приняв в качестве обобщенных координат моменты в упругих звеньях, получим следующие уравнения движения:
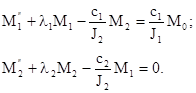
После преобразования по Лапласу получим
(s2+l1)M1(s) - 
M2(s) = 
M0(s);
(s2+l2)M2(s) - 
M1(s) = 0.
Отсюда искомые передаточные функции
W1(s) = = 
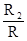; W2(s) = = 
,
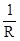где R=R1R2- g12; R1= s2+l1; R2= s2+l2;
g12=c1c2/J22; l1=c1(1/J1+1/J2); l2=c2(1/J2+1/J3);
Анализ передаточных функций показывает, что их можно записывать непосредственно по виду динамической модели без составления уравнений движения.
Структура передаточной функции динамической модели имеет следующий вид:
W(s) = K· B / C.
|
|
|
Переменная K учитывает параметры модели, расположенные на пути прохождения сигнала от входной до выходной координат. Переменная В соответствует характеристическому определителю части динамической системы (подсистемы), расположенной вне пути прохождения сигнала. Переменная С соответствует характеристическому определителю части динамической модели, расположенной на пути прохождения входного сигнала. Если за входной сигнал принято внешнее воздействие. то С соответствует характеристическому определителю всей системы.
При анализе пути прохождения сигнала массы, расположенные на пути его прохождения, считаются закрепленными, а упругие звенья – разорванными, что равноценно приравниванию нулю соответствующих координат. Если имеется несколько путей прохождения сигнала, то передаточная функция равна сумме передаточных функций, определяемых отдельно для каждого пути.
 |
Ниже приведены примеры некоторых передаточных функций между моментами Mi и углами поворота масс ji для динамических моделей, показанных на рис. 14. Упруго-диссипативная характеристика gi =bis+ci учитывает диссипативные (коэффициент bi) и упругие (коэффициент сi) свойства i-го звена.
а)
б)
 |
в)
 |
Рис. 14. Динамические модели различных типов
Неразветвленная динамическая модель (рис 14 а).
= 
= 
= 
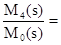
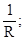
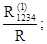
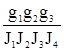
Разветвленная динамическая модель (рис 14 б).
W02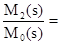(s) = 
W03(s) =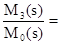 
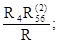
Динамическая модель с дифференциальным разветвлением (рис. 14 в).
W02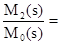(s) = 
W03(s) =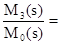 
W04(s) = 
Частотные характеристики объекта
Частотные характеристики оценивают свойства объекта при воздействии на него гармонических возмущений. В дальнейшем ограничимся рассмотрением только амплитудных частотных характеристик (АЧХ) и собственных частот объектов. Частотные характеристики самым тесным образом связаны с передаточными функциями. Для получения частотных характеристик достаточно в передаточной функции W(s) заменить s на jw. В результате получается комплексная частотная характеристика (КЧХ) W(jw). Все остальные характеристики являются ее частными случаями.
|
|
|
|
|
|
