 |
Исследование функции по общей схеме.
|
|
|
|
1. Область определения функции f (x) – полностью может быть указана после исследования функции на непрерывность.
2. Непрерывность и точки разрыва функции f (x) исследуются по схеме:
> iscont(f, x=-infinity..infinity);
> d1:=discont(f,x);
> d2:=singular(f,x);
В результате наборам переменным d1 и d2 будут присвоены значения x -координат в точках разрыва 1 и 2-го родов (если они будут найдены).
3. Асимптоты. Точки бесконечных разрывов определяют вертикальные асимптоты графика f (x). Уравнение вертикальной асимптоты имеет вид:
> yr:=d2;
Поведение функции f (x) на бесконечности характеризуется наклонными асимптотами (если они есть). Уравнение наклонной асимптоты y=kx+b, где коэффициенты вычисляются по формулам:
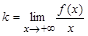и 
.
Аналогичные формулы для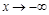 
. Поэтому нахождение наклонных асимптот можно провести по следующей схеме:
> k1:=limit(f(x)/x, x=+infinity);
> b1:=limit(f(x)-k1*x, x=+infinity);
> k2:=limit(f(x)/x, x=-infinity);
> b2:=limit(f(x)-k2*x, x=-infinity);
Часто оказывается, что k1=k2 и b1=b2, в этом случае будет одна асимптота 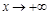при 
и при 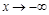. С учетом этого составляется уравнение асимптоты
> yn:=k1*x+b1;
4. Экстремумы. Исследование функции f (x) на экстремумы можно проводить по схеме:
> extrema(f(x), {}, x, ’s’);
> s;
> fmax:=maximize(f(x), x);
> fmin:=minimize(f(x), x);
После выполнения этих команд будут найдены координаты (x, y) всех максимумов и минимумов функции f (x).
Построение графика.
Построение графика функции f (x)– это окончательный этап исследования функции. На рисунке помимо графика исследуемой функции f (x) должны быть нанесены все ее асимптоты пунктирными линиями, подписаны координаты точек max и min. Приемы построения графиков нескольких функций и нанесения надписей были рассмотрены в теме III.
Задание 3.3.
1. Провести полное исследование функции 
по общей схеме. Сначала перейдите в текстовый режим и наберите “Исследование функции: “. Затем вернитесь в режим командной строки и наберите команды:
|
|
|
> f:=x^4/(1+x)^3:
В текстовом режиме наберите “Непрерывность функции”. В режиме командной строки и наберите:
> readlib(iscont): readlib(discont):
readlib(singular):
> iscont(f, x=-infinity..infinity);
false
Это означает, что функция не является непрерывной. Перейдите в текстовый режим и наберите “Нахождение точек разрыва”. Вернитесь в режим командной строки и наберите:
> discont(f,x);
{-1}
Конвертировать полученное значение точки разрыва типа set в число можно командой convert, добавив вторую опцию, например, `+`. Обратите внимание на обратные кавычки, которые набираются клавишей, расположенной выше клавиши табуляции.
> xr:=convert(%,`+`);
xr:= -1
Перейдите в текстовый режим и наберите: “Получена точка бесконечного разрыва x =-1”. С новой строки наберите: “Нахождение асимптот.”. Перейдите на новую строку и наберите “Уравнение вертикальной асимптоты: x =-1” (это можно сделать, поскольку вертикальные асимптоты возникают в точках бесконечного разрыва). С новой строки наберите: “Коэффициенты наклонной асимптоты:”. Перейдите в режим командной строки и наберите:
> k1:=limit(f/x, x=+infinity);
k1:=1
> b1:=limit(f-k1*x, x=+infinity);
b1:= -3
> k2:=limit(f/x, x=-infinity);
k2:=1
> b2:=limit(f-k2*x, x=-infinity);
b2:= -3
В этом случае коэффициенты наклонных асимптот пр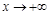и 
и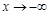 
оказались одинаковыми. Поэтому перейдите в текстовый режим и наберите “Уравнение наклонной асимптоты:”. Затем в новой строке прейдите в режим командной строки и наберите:
> y=k1*x+b1;
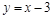
В текстовом режиме наберите “Нахождение экстремумов”. В новой строке наберите команды:
> readlib(extrema): readlib(maximize):
readlib(minimize):
> extrema(f,{},x,'s');s;
{ 
, 0}
{{ x = -4},{ x =0}}
Поскольку функция имеет разрыв, то при поиске максимума и минимума следует указать интервал, в который не должна входить точка разрыва.
> fmax:=maximize(f,{x},{x=-infinity..-2});
|
|
|
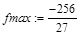
> fmin:=minimize(f,{x},{x=-1/2..infinity});
В текстовом режиме наберите результат исследования в виде:
“Максимум в точке (-4, -256/27); минимум в точке (0, 0).”
2. Построить график функции 
и ее асимптоту, указать координаты точек экстремума. Оформление каждого этапа исследования функции проделать также как и при выполнении предыдущего задания. Самостоятельно загрузите из стандартной библиотеки все необходимые команды.
> restart: y:=arctan(x^2):
> iscont(y, x=-infinity..infinity);
true
> k1:=limit(y/x, x=-infinity);
k1:=0
> k2:=limit(y/x, x=+infinity);
k2:=0
> b1:=limit(y-k1*x, x=-infinity);
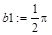
> b2:=limit(y-k1*x, x=+infinity);
> yh:=b1;
> extrema(y,{},x,'s');s;
{0}
{{ x =0}}
> ymax:=maximize(y,{x}); ymin:=minimize(y,{x});
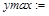
> with(plots): yy:=convert(y,string):
> p1:=plot(y,x=-5..5, linestyle=1, thickness=3,
color=BLACK):
> p2:=plot(yh,x=-5..5, linestyle=1,thickness=1):
> t1:=textplot([0.2,1.7,"Асимптота:"],
font=[TIMES, BOLD, 10], align=RIGHT):
> t2:=textplot([3.1,1.7,"y=Pi/2"],
font=[TIMES, ITALIC, 10], align=RIGHT):
> t3:=textplot([0.1,-0.2,"min:(0,0)"],
align=RIGHT):
> t4:=textplot([2,1,yy], font=[TIMES, ITALIC,
10], align=RIGHT):
> display([p1,p2,t1,t2,t3,t4]);
§4. Интегрирование
|
|
|
