 |
Действия с матрицами
|
|
|
|
Определение матрицы.
Для определения матрицы в Maple можно использовать команду matrix(n, m, [[a11,a12,…,a1n], [a21,a22,…,a2m],…, [an1,an2,…,anm]]), где n - число строк, m – число столбцов в матрице. Эти числа задавать необязательно, а достаточно перечислить элементы матрицы построчно в квадратных скобках через запятую. Например:
> A:=matrix([[1,2,3],[-3,-2,-1]]);

В Maple матрицы специального вида можно генерировать с помощью дополнительных команд. В частности диагональную матрицу можно получить командой diag. Например:
> J:=diag(1,2,3);

Генерировать матрицу можно с помощью функции f (i, j) от переменных i, j – индексов матрицы: matrix(n, m, f), где где n - число строк, m – число столбцов. Например:
> f:=(i, j)->x^i*y^j;

> A:=matrix(2,3,f);

Число строк в матрице А можно определить с помощью команды rowdim(A), а число столбцов – с помощью команды coldim(A).
Арифметические операции с матрицами.
Сложение двух матриц одинаковой размерности осуществляется теми же командами, что и сложение векторов: evalm(A+B) или matadd(A,B). Произведение двух матриц может быть найдено с помощью двух команд:
1) evalm(A&*B);
2) multiply(A,B).
В качестве второго аргумента в командах, вычисляющих произведение, можно указывать вектор, например:
> A:=matrix([[1,0],[0,-1]]);
> B:=matrix([[-5,1], [7,4]]);


> v:=vector([2,4]);

> multiply(A,v);

> multiply(A,B);

> matadd(A,B);

Команда evalm позволяет также прибавлять к матрице число и умножать матрицу на число. Например:
> С:=matrix([[1,1],[2,3]]):
> evalm(2+3*С);

Определители, миноры и алгебраические дополнения. Ранг и след матрицы.
Определитель матрицы А вычисляется командой det(A). Команда minor(A,i,j) возвращает матрицу, полученную из исходной матрицы А вычеркиванием i -ой строки и j -ого столбца. Минор Mij элемента aij матрицы А можно вычислить командой det(minor(A,i,j)). Ранг матрицы А вычисляется командой rank(A). След матрицы А, равный сумме ее диагональных элементов, вычисляется командой trace(A). 7
|
|
|
> A:=matrix([[4,0,5],[0,1,-6],[3,0,4]]);

> det(A);
> minor(А,3,2);

> det(%);
-24
> trace(A);
Обратная и транспонированная матрицы.
Обратную матрицу А -1, такую что А -1 А = АА -1= Е, где Е - единичная матрица, можно вычислить двумя способами:
1) evalm(1/A);
2) inverse(A).
Транспонирование матрицы А – это изменение местами строк и столбцов. Полученная в результате этого матрица называется транспонированной и обозначается А'. Транспонированную матрицу А' можно вычислить командой transpose(A).
Например, используя заданную в предыдущем пункте матрицу А, найдем ей обратную и транспонированную:
> inverse(A);

> multiply(A,%);

> transpose(A);

Выяснение типа матрицы.
Выяснить положительную или отрицательную определенность матрицы можно при помощи команды definite(A,param), где param может принимать значения: 'positive_def' – положительно определена (A >0), 'positive_semidef' – неотрицательно определенная  , 'negative_def' – отрицательно определенная (A <0), 'negative_semidef' - неположительно определенная
, 'negative_def' – отрицательно определенная (A <0), 'negative_semidef' - неположительно определенная  . Результатом действия будет константа true – подтверждение, false – отрицание сделанного предположения. Например:
. Результатом действия будет константа true – подтверждение, false – отрицание сделанного предположения. Например:
> A:=matrix([[2,1],[1,3]]);

> definite(А,'positive_def');
true
Проверить ортогональность матрицы А можно командой orthog(A).
> В:=matrix([[1/2,1*sqrt(3)/2],
[1*sqrt(3)/2,-1/2]]);

> orthog(В);
true
Функции от матриц.
Возведение матрицы А в степень n производится командой evalm(A^n). Вычисление матричной экспоненты  возможно с помощью команды exponential(A). Например:
возможно с помощью команды exponential(A). Например:
> Т:=matrix([[5*a,2*b],[-2*b,5*a]]);

> exponential(Т);

> evalm(Т^2);

Задание 2.
1. Даны матрицы:  ,
,  ,
,  . Найти: (AB) C, det A, det B, det C, det[(AB) C ]. Наберите:
. Найти: (AB) C, det A, det B, det C, det[(AB) C ]. Наберите:
> with(linalg):restart;
> A:=matrix([[4,3],[7,5]]):
> B:=matrix([[-28,93],[38,-126]]):
> C:=matrix([[7,3],[2,1]]):
> F:=evalm(A&*B&*C);

> Det(A)=det(A); Det(B)=det(B); Det(C)=det(C);
Det(F)=det(F);
Det(A)=-1
Det(B)=-6
Det(C)=1
Det(F)=6
|
|
|
2. Дана матрица 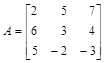 , найти: det A,
, найти: det A,  , A’, det(M 22). Наберите:
, A’, det(M 22). Наберите:
> A:=matrix([[2,5,7],[6,3,4],[5,-2,-3]]);
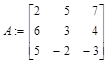
> Det(A)=det(A);
Det(A)=-1
> transpose(A);

> inverse(A);

> det(minor(A,2,2));
-41
3. Найти ранг матрицы  .
.
> A:=matrix([[8,-4,5,5,9], [1,-3,-5,0,-7],
[7,-5,1,4,1], [3,-1,3,2,5]]):
> r(A)=rank(A);
r(A)=3
4. Вычислить  , где
, где  .
.
> exponential([[3,-1],[1,1]]);

5. Дана матрица  . Найти значение многочлена
. Найти значение многочлена  .
.
> A:=matrix([[5,1,4],[3,3,2],[6,2,10]]):
> P(A)=evalm(A^3-18*A^2+64*A);

§3. Спектральный анализ матрицы
|
|
|


