 |
Контрольные задания.
|
|
|
|
1. Вычислите предел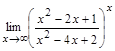 
.
2. Найти пределы функции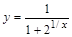 
при 
и при 
.
3. Найти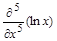 
.
4. Найти точки разрыва функции 
.
5. Найти экстремумы функции 
, 
и указать их характер.
6. Провести полное исследование функции 
.
7. Построить график функции 
с указанием координат экстремумов.
8. Вычислить неопределенный интеграл 
.
9. Вычислить несобственный интеграл 
при a >0 b >0 для случаев a > b, a = b, a < b.
10. Численно найти интеграл 
.
11. Полностью проделать все этапы вычисления интеграла 
по частям.
12. Вычислить интеграл 
с помощью универсальной подстановки tg(x /2)= t.
Контрольные вопросы.
1. Что такое команды прямого и отложенного исполнения? Опишите их действия.
2. С помощью какой команды вычисляются пределы? Какие у нее параметры?
3. Какие команды позволяют найти производную функции?
4. Опишите команды, позволяющие исследовать функцию на непрерывность.
5. Какая последовательность команд необходима для нахождения max и min функции с указанием их координат (x, y)?
6. Какие недостатки имеют команды maximize, minimize и extrema?
7. Опишите общую схему исследования функции и построение ее графика в Maple.
8. Какие команды производят аналитическое и численное интегрирование? Опишите их параметры.
9. С помощью каких команд вводятся ограничения на параметры для вычисления интегралов, зависящих от параметров?
10. Для чего предназначен пакет student?
11. Опишите команду интегрирования по частям.
12. Опишите команду интегрирования методом замены переменных.
V. Линейная алгебра
1. Векторная алгебра.
2. Действия с матрицами.
3. Спектральный анализ матрицы.
4. Системы линейных уравнений. Матричные уравнения.
§1. Векторная алгебра
Основная часть команд для решения задач линейной алгебры содержится в библиотеке linalg. Поэтому перед решением задач с матрицами и векторами следует загрузить эту библиотеку командой with(linalg).
|
|
|
Способы задания векторов.
Для определения вектора в Maple используется команда vector([x1,x2,…,xn]), где в квадратных скобках через запятую указываются координаты вектора. Например:
> x:=vector([1,0,0]);
x:=[1, 0, 0]
Координату уже определенного вектора x можно получить в строке вывода, если ввести команду x[i], где i - номер координаты. Например, первую координату заданного в предыдущем примере вектора можно вывести так:
> x[1];
Вектор можно преобразовать в список и, наоборот, с помощью команды convert(vector, list) или convert(list, vector).
Сложение векторов.
Сложить два вектора a и b можно с помощью двух команд:
1) evalm(a+b);
2) matadd(a,b).
Команда add позволяет вычислять линейную комбинацию векторов a и b: 
, где 
- скалярные величины, если использовать формат: matadd(a,b,alpha,beta).
Скалярное, векторное произведение векторов и угол между векторами.
Скалярное произведение двух векторов 
вычисляется командой dotprod(a,b).
Векторное произведение двух векторов 
вычисляется командой crossprod(a,b).
Угол между двумя векторами a и b вычисляется с помощью команды angle(a,b).
Норма вектора.
Норму (длину) вектора 
, которая равна 
, можно вычислить с помощью команды norm(а,2).
Можно нормировать вектор а с помощью команды normalize(a), в результате выполнения которой будет получен вектор единичной длины 
.
Нахождение базиса системы векторов. Ортогонализация системы векторов по процедуре Грамма-Шмидта.
Если имеется система n векторов 
, то с помощью команды basis([a1,a2,…,an]) можно найти базис этой системы.
При помощи команды GramSchmidt([a1,a2,…,an]) можно ортогонализовать систему линейно-независимых векторов .
Задание 1.
1. Даны два вектора: 
и 
. Найти 
и угол между a и b. Для решения этой задачи наберите:
> with(linalg):
|
|
|
> a:=([2,1,3,2]); b:=([1,2,-2,1]);
a:=[2,1,3,2]
b:=[1,2,-2,1]
> dotprod(a,b);
> phi=angle(a,b);
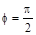
2. Найти векторное произведение 
, а затем скалярное произведение 
, где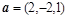 
, 
.
> restart; with(linalg):
> a:=([2,-2,1]); b:=([2,3,6]);
a:=[2,-2,1]
b:=[2,3,6]
> c:=crossprod(a,b);
c:=[-15,-10,10]
> dotprod(a,c);
3. Найти норму вектора .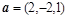
> restart; with(linalg):
> a:=vector([1,2,3,4,5,6]): norm(a,2);
4. Из системы векторов: 
, 
, 
, 
, 
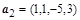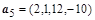выделить базис и ортогонализовать его по процедуре Грамма-Шмидта:
> restart; with(linalg):
> a1:=vector([1,2,2,-1]):
a2:=vector([1,1,-5,3]):
a3:=vector([3,2,8,7]): a4:=vector([0,1,7,-4]):
a5:=vector([2,1,12,-10]):
> g:=basis([a1,a2,a3,a4,a5]);
g:= [ a1, a2, a3, a5 ]
> GramSchmidt(g);
[[1,2,2,-1], [2,3,-3,2], 
, 
|
|
|
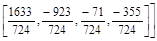
