 |
Объем понятия
|
|
|
|
Вторая логическая характеристика каждого понятия — объем — это те мыслимые в понятии объекты, ради выделения которых из всех других объектов и образуется содержание понятия.
Поскольку объем понятия представляет собой множество, то нам придется овладеть некоторыми самыми элементарными сведениями из теории множеств.
Первоначальному понятию теории множеств — множеству — нельзя дать определения. Его можно только пояснить. Под множеством в дальнейшем мы будем иметь в виду совокупность объектов, которые мы по тем или иным основаниям способны мыслить вместе.
Люди, студенты, звезды, понятия — все эти предметы, мыслимые вместе, образуют множества. Коллектив, созвездие, полк — это тоже множества людей или звезд. Множество может быть задано двояко: 1) при помощи некоторого признака или 2) при помощи списка. В предложении — «Студенты Боброва, Курпаков и Юдина могут покинуть аудиторию» — множество задается списком. В предложении — «Студенты, сдавшие контрольную работу, могут покинуть аудиторию» — множество задается при помощи общего признака.
Таким образом, любые объекты, которые мы мыслим вместе и которые мы можем объединить либо списком, либо при помощи общего признака, будут составлять множество.
Об отдельном объекте, из числа тех, что образуют данное множество, мы будем говорить, что этот объект входит в данное множество или объекта принадлежит данному множеству.
Объект a будем называть элементом множества A, если он входит в множество A.
Этот факт мы будем записывать следующим образом:
.
Множество А будем называть подмножеством множества В, если каждый элемент А в то же время является элементом В.
|
|
|
Это мы будем записывать так:
Множество А будем называть собственным подмножеством множества С, если А — подмножество С и существует хотя бы один элемент С, который не является элементом множества A.
Это мы будем записывать так:
.
Для обозначения множеств мы будем использовать те же прописные буквы начала латинского алфавита, набранные курсивом, что и для обозначения понятий. Основанием для этого служит тот факт, что содержание понятия есть признак, по которому можно образовать множество. К тому же из контекста употребления этих обозначений всегда будет ясно, о чем идет речь: о понятии или о множестве.
Для понимания теории понятия нам понадобится некоторое представление о простых операциях с множествами таких, как пересечение и объединение множеств, а также дополнение к множеству.
Пересечением множеств A и B будем называть множество тех элементов, которые одновременно входят в A и B.
Более формально: 
множество a таких, что и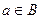 
.
Например. Пересечением множеств студентов и отличников будет множество студентов-отличников, а пересечением множеств греческих богов и кузнецов будет множество, состоящее из единственного элемента — бога-кузнеца Гефеста. Пересечением множества книг и учебных пособий будет множество учебников.
Объединением множеств A и B будем называть множество элементов, которые входят в A или в B.
Более формально: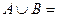 
множество a таких, что или .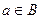
Например. Объединением множеств газет и журналов будет множество периодических изданий, а объединением множеств четных и нечетных чисел — множество натуральных чисел.
Операции с множествами удобно иллюстрировать при помощи графических схем, в которых множества представляются в виде кругов, и предпойагается, что в этих кругах заключены все элементы данного множества. Такие круги называются кругами Эйлера, по имени немецкого математика Леонарда Эйлера, который в 1762 году приспособил эту геометрическую фигуру для логических целей.
|
|
|
Например. Множество стульев мы изобразим следующим образом:
 |
Рис. 1
Рис. 1
Внутри круга, изображенного на рис. 1, находятся все возможные стулья.
Отдельный элемент будем обозначать точкой в круге, единичное множество — кругом.
Например. Множество русских царей изобразим при помощи круга, а отдельный элемент, например, Александра П – точкой в круге:
 |
Рис. 2
Пересечение множеств студентов и отличников будет выглядеть таким образом:
Рис. 3
Заштрихованная часть — это множество тех элементов, которые одновременно принадлежат множествам студентов и отличников. Таким образом, в заштрихованной части, называемой пересечением множеств, находятся все студенты-отличники.
Объединение множеств студентов и отличников будет выглядеть следующим образом:
Рис. 4
Заштрихованная обласрь представляет собой объединение этих множеств, т. е. множество студентов или отличников. В него входят все студенты, а также все отличники. Каждый элемент является студентом или отличником, а некоторые элементы – одновременно студентами и отличниками (как видно на рис. 4).
Чтобы ввести еще одну важную операцию с множествами, нам понадобится одно новое понятие. Представим себе множество всех объектов, т. е. такое множество, для которого любое другое множество объектов, кроме него самого, является его собственным подмножеством.
Множество всех объектов U назовем универсальным множеством.
Поскольку любое множество A является подмножеством этого множества, то мы для любого множества можем рассмотреть операцию, дополняющую это множество до универсального. Эта операция так и называется — дополнение. Графически ее можно изобразить следующим образом:
Рис. 5
Заштрихованная часть представляет собой дополнение A. Символически дополнение будем изображать так - 
.
Можно рассматривать дополнения не тмлько к отдельному множеству, но и к пересечениям и объединениям множеств.
Существуют простые взаимоотношения между пересечением, объединением и дополнением множеств:
|
|
|
Кроме универсального, существует еще одно специальное и единственное множество, которое не содержит ни одного элемента.
Множество, не содержащее ни одного элемента, называется пустым множеством.
и будем обозначать его 
Существуют простые взаимоотношения произвольных множеств с универсальным и пустым:
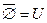
Операции пересечения и объединения могут быть, как в арифметике операции умножения и сложения обобщены на случай более чем двух множеств. Так, мы будем писать
.
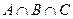имея при этом в виду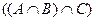 
.
То же самое и для объединения.
Познакомившись с первоначальными понятиями теории множеств, перейдем к объему понятий.
Пусть множество A составляет объем понятия A.
Тогда собственное подмножество B множества A будем называть частью объема понятия A.
Проще говоря, часть объема понятия — это более одного элемента объема понятия, но не все.
Элементом объема понятия будем называть элемент множества, составляющего объем понятия.
Чтобы эффективно оперировать в дальнейшем с объемами понятий, следует иметь в виду следующее правило объема:
Каждый элемент объема понятия имеет все признаки, перечисленные в содержании понятия.
Итак, если вы хотите установить, является ли некоторый предмет элементмм объема данного понятия, проверьте, имеет ли он все признаки, которые вы мыслите в (основном) содержании данного понятия. Это правило особенно существенно для понятий типа: коллектив, созвездие, преступная группа, множество, лес и т. п. Обратите внимание, что пользуясь этим правилом, можно объяснить, почему отдельные люди, звезды, преступники, предметы, деревья не являются элементами объема этих понятий, и заодно понять, что же является элементами их объема.
§ 3. Обобщение и ограничение понятий
Понятия широко используются в нашем обычном и в особенности научном мышлении не только с целью ясного мышления различных множеств объектов, но и для придания определенности различным действиям мышления. В этом параграфе мы переходим к рассмотрению действий с понятиями в нашем мышлении, Действия с понятиями (и другими видами мысли) мы будем называть логическими операциями. Две элементарные логические операции будут рассмотрены в этом параграфе.
|
|
|
Ав: Здравствуйте, друзья! Я бы хотел, чтобы вы послушали один диалог. Сейчас включу магнитофон. Слушайте.
(Треск, шум уличного движения, звук шагов. Становится понятно, что запись производилась в тайне, по крайней мере, от одного из участников разговора).
Д (обращаясь к Е и Ж): Слушайте, вы знаете, что случилось с нашим приятелем Х?
Е и Ж (хором): Нет.
Д: Он же в Учреждении работает Должностным Лицом. А у них всегда очередь за Услугой. И вот он взял деньги у У из рук в руки за оказанную его учреждением вне очереди Услугу.
Е: Молодец Х! Сделал доброе дело. Ведь У доволен?
Д: Доволен.
Е: И Х доволен. Значит, всем хорошо.
Ж: Да, но это де преступление.
Как вам такой диалог? Как вы думаете, о чем идет речь?
Сс: Взять деньги за оказание Услуги вне очереди — это на юридическом языке называется взяткой, а взятка — это преступление. Поэтому Ж — прав.
Ст: Прав-то прав. Но уважаемый Автор, видимо, нас не о том спрашивает. Он имеет в виду что-нибудь логическое. Ведь Е и Ж реагируют на одну и ту же мысль по-разному. Это, видимо, означает, что они как-то по-разному к ней подходят.
Ав: Правильно! Вы же заметили, что об одном и том же деянии один гоаорит, что это доброе дело, а другой — что это преступление.
Сс: Ну, видимо, иногда преступление может быть добрым делом.
Ав: Давайте не будем вступать в дискуссию и предположим, что так не бывает.
Ст: Давайте. На мой взгляд, В и С не согласны в том, под какое другое понятие подвести то, что сделал Х.
Сс: Они согласны в том, что Х взял взятку, но расходятся в оценке самой взятки.
Ав: А «взятка» — это понятие?
Сс: Конечно!
Ав: А «доброе дело» и «преступление» — это понятия?
Ст: Ну, насчет преступления мы знаем точно. А «доброе дело» также из всего круга дел выделяет и обобщает дела добрые, поэтому это - тоже понятие.
Ав: Значит, о чем идет речь?
Сс: О том, что Е и Ж одно понятие — «взятка» — подводят под два разных понятия: «доброе дело» и «преступление».
Ав: Мне здесь не нравится термин «подводят».
Ст: А что, у Вас есть лучший?
Ав: Есть! Обобщение.
Сс: А, действительно, разногласие же в том, какое понятие является более общим по отношению к понятию «взятка», поэтому термин «обобщение» здесь подходит.
Ст: Да ну их, эти термины! Вот правильно ли я понял, что всякий раз, когда мы хотим дать оценку некоторому предмету, явлению и т. п., то мы подводим его под более общее понятие?
|
|
|
Ав: Я думаю, что вы поняли правильно.
Сс: И это можно сделать правильно и неправильно.
Ав: Конечно. Мы же видим, кто из них прав.
Этот диалог показал нам, что в нашем мышлении регулярно встречается задача перехода от некоторого понятия к более общему. Мы сталкиваемся с ней каждый раз, как хотим подвести некоторый вид класс предметов или даже единичный предмет под какую-либо категорию, или дать им общую оценку. Вопрос: «Всякое ли решение правительства справедливо? » означает, что мы хотим узнать, можно ли от понятия «решение правительства» правильно перейти к понятию «справедливое деяние». Утверждение «Преступление – это зло» означает, что от понятия «преступление» можно правильно перейти к понятию «злое деяние». Нам осталось разобраться, как же совершается этот переход, и как его совершать правильно.
Обобщение — это логическая операция, состоэщая в переходе от понятия A к понятию B, при котором объем понятия A оказывается частью объема понятия B.
Если прибегнуть к кругам Эйлера, то получится следующая картинка:
Рис. 1
Тогда сущность спора между Е и Ж из нашего диалога изобразится так:
Рис. 2
Осталось только выяснить, как это делать правильно. Мы уже рассмотрели обобщение понятия с точки зрения объема. Теперь посмотрим, что происходит при обобщении с содержанием понятия.
Напомним, что в сложном признаке, составляющем содержание нонятия, простые признаки могут соединяться двояко: 1) при помощи союза «и» или 2) при помощи союза «или». Разные способы соединения простых признаков обусловливают разные стратегии работы с признаками при обобщении понятий.
1) Простые признаки соединены при помощи союза «и». Это означает, что они одновременно присущи всем элементам объема данного понятия. Поэтому, если мы хотим перейти к другому понятию с «большим» объемом, то нам надо отбросить некоторый признак. Тогда наше условие, налагаемое на предметы, станет слабее, а это означает, что ему будет удовлетворять «большее» множество предметов.
Пример. Прямоугольный треугольник — плоская геометрическая фигура, которая ограничена тремя сторонами и один из углов которой является прямым.
Курсивом выделен признак, служащий основным содержанием понятия. Если мы отбросим из него простой признак «иметь прямой угол», то получим новое понятие: «плоская геометрическая фигура, ограниченная тремя сторонами». Нетрудно заметить, что в объем этого понятия будут входить уже не только прямоугольные треугольники, но и остро- и тупоугольные треугольники, т. е. все треугольники вообще. Получилось, что, отбросив признак «иметь прямой угол», мы перешли к новому понятию «треугольник», объем которого включает объем первоначального понятия «прямоугольный треугольник». Именно это имелось в виду, когда несколько выше говорилось о том, что при отбрасывании признака, связанного с другими признаками, входящими в содержание понятия через «и», мы получаем новое понятие с «большим» объемом.
Общий вывод:
Обобщение понятий, содержание которых состоит из признаков, соединенных союзом «и», происходит путем отбрасывания простых признаков.
2) Простые признаки в содержании понятия соединены при помощи союза « или ». Это означает, что каждый отдельный простой признак, входящий в содержание понятия, может быть присущ не всем элементам объема этого понятия, а только всем элементам некоторой его части, т. е. отдельному виду, а всем вместе присуще только сложный признак, соединяющий более простые признаки херез «или».
Пример. Существительное — это часть речи, обозначающая предмет и отвечающая на вопрос «кто? » или «что? ».
В этом примере признак «отвечать на вопрос «кто? » или «что? » является сложным признаком, в котором простые признаки «отвечать на вопрос «кто? » и «отвечать на вопрос «что? » соединены при помощи союза «или». Это означает, что определенному виду существительных присущ признак «отвечать на вопрос «кто? » и мы знаем, что это — одушевленные существительные, а другому виду существительных присущ приенак — «отвечать на вопрос «что? », но не присущ признак «отвечать на вопрос «кто? », это — неодушевленные существительные.
Очевидно, что если отбросить какой-либо из этих признаков, то мы получим новое понятие, объем которого будет не «больше», а «меньше» объема исходного, точнее говоря, объем нового понятия будет составлять часть объема исходного понятия. Обобщения при этом, конечно, не получится. Однако отсюда мы можем заключить, что мы добьемся увеличения объема исходного понятия, если присоединим к его содержанию новый признак через «или».
Пример. Автократия — это форма правления, при которой власть полностью сосредоточена в руках единоличного главы государства.
Если мы в этом примере добавим через «или» к содержанию понятия признак «власть частично сосредоточена в руках единоличного главы государства», то получим понятие со следующим основным содержанием: «форма правления, при которой власть полностью или частично сосредоточена в руках единоличного главы государства». Это уже будет понятие монархии, одним из видов которой является автократия.
Общий вывод:
Обобщение понятий может происходить путем добавления к содержанию понятия признаков при помощи союза «или».
В определении операции обобщения понятий входят только пары понятий. Однако мы можем попытаться далее обобщить понятие B из нашего определения. Тогда возникнет цепь обобщений, которая может быть достаточно длинной.
Например. Рассмотрим следующую последовательность понятий: кража автомобиля, кража, хищение, преступление, деяние.
Графически это выглядит так:
Рис. 3
Заметим, что все объекты, составляющие объем первого понятия «кража автомашин», входят в объем всех более общих понятий, и это верно для каждого последующего понятия. Этот принцип важен, чтобы отличать обобщение от отношения части к целому.
Цепочка:
юридический факультет 
факультет
представляет собой обобщение, потому что объем понятия «юридический факультет» представляет собой часть объема понятия «факультет». В то же время цепочка:
факультет 
университет
не представляет собой обобщения, так как объем понятия «факультет» не является частью объема понятия «университет». В них вообще выделяются разные предметы. Факультет является частью предмета «университет». Различить эти операции довольно просто, если правильно задать вопрос об отношениях рассматриваемых понятий. Для первой пары понятий такой вопрос будет выглядеть следующим образом: «Является ли юридический факультет факультетом? » Ответ на него тривиально прост: «да». Для второй пары понятий следует задать такой же вопрос: «Является ли факультет университетом? ». Ответ на этот вопрос также прост: «нет». Отсюда мы можем получить правило:
Переход от понятия А к понятию В является обобщением, если ответ на вопрос: «Верно ли, что А есть В? » утвердителен.
Рассматривая обобщения понятия «кража автомобиля», мы, в конце концов, пришли к понятию «деяние». В пределах правовой теории нам дальше идти некуда, любое дальнейшее обобщение выводит за пределы правовой теории. Это — самое широкое, самое общее понятие в этой области науки.
Предельно общее понятие в данной области знания называется категорией данной области знания.
Каждая наука обладает своей системой категорий, т. е. понятий, которые уже нельзя обобщить в пределах данной науки.
В нашей логической онтологии имеются такие категории, как предмет, свойство и отношение. В логике — такие категории, как понятие, суждение, умозаключение, поскольку, если мы обобщим суждение и понятие до понятия мысли, то выйдем за пределы логики в область философии.
Ав: Так, вы еще не ушли. Прочли то, что я написал об обобщении?
Сс: Да.
Ав: Тогда послушайте еще один диалог:
Обвинитель: Х совершил преступление.
Защитник: Какое же это преступление?!
Обвинитель: Как же? Х использовал свое служебное положение для вымогательства денег за Услугу, а это — взятка.
Ав: О чем здесь речь?
Сс: Обвинитель хотел обойтись очень общей оценкой деяния Х, а защитник заставил его конкретизировать свое обвинение, ограничить его, потому что из первого высказывания обвинителя совершеннм непонятно, что сделал Х.
Ав: Что же тогда сделал обвинитель?
Ст: Я думаю, что он сделал какое-то действие, обратное обобщению. Мы ведь знаем, что понятие «преступление» представляет собой обобщение понятия «взятка». А он поступил как раз наоборот.
Ав: Правильно. Та мыслительная операция, которую совершил Обвинитель, называется ограничение. Его исходный тезис стал убедительнее, поскольку он стал конкретнее. Обвинитель от более общего понятия «преступление» перешел к более конкретному понятию «взятка».
В нмвом диалоге мы встретились с логической операцией, называемой ограничение.
Ограничение — это логическая операция, состоящая в переходе от понятия A к другому понятию B, при котором объем понятия B оказывается частью объема понятия A.
Что же при этом делается с содержанием? Опять же, изменение содержания зависит от структуры признаков, составляющих содержание, т. е. от того, соединены они через «и» или через «или».
Соображения, аналогичные тем, что были изложены при обсуждении операции обобщения, показываьт, что для ограничения понятия нам достаточно отбросить из его содержания признак, соединенный с другими через «или».
Пример. Рассмотрим приведенное выше содержание понятия «имя существительное». Для его ограничения достаточно отбросить признак «отвечать на вопрос «что? ». Тогда мы получим понятие со следующим содержанием: «часть речи, обозначающая предмет и отвечающая на вопрос «кто? », т. е. понятие одушевленного существительного.
Общий вывод:
Ограничение понятий, содержание которых состоит из признаков, соединенных союзом «или», происходит путем отбрасывания простых признаков.
Те же соображения подсказывают нам следующий общий вывод:
Ограничение понятий может происходить путем присоединения признаков через союз «и».
Например. Если мы к понятию «треугольник» присоединим признак «иметь прямой угол», то мы получим понятие «прямоугольный треугольник», являющееся ограничением первоначального понятия.
Как видите, ситуация противоположна обобщению, или, как сказал бы логик, двойственна. Если продолжать сколь угодно далеко операцию ограничения некоторого понятия, то в конце концов его пределом окажется понятие, объем которого представляет собой множество, состоящее из одного объекта.
Пределом ограничения понятия A является понятие В, объем которого является частью объема понятия A и состоит не более, чем из одного объекта.
Например. Рассмотрим следующую цепь ограничений: небесное тело → спутник → спутник Земли → естественный спутник Земли. Естественный спутник Земли – понятие, в объем которого входит только один предмет – Луна.
Познавательный смысл обобщения и ограничения заключается в том, что обобщение — способ движения к более общему знанию, а ограничение — к более конкретному знанию. Эти процессы нам часто приходится совершать и в обычном мышлении, и в ходе научных исследований, и при изложении научных положений.
|
|
|
