 |
Структура силлогизма
|
|
|
|
|-, |-.
Пример.
Из ложности суждения “Некоторые люди способны изменять ход истории” следует ложность суждения “Все люди способны изменять ход истории” ( 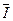 |-
|-  ).
).
Пример.
Из ложности суждения “Некоторые люди неспособны к самосовершенствованию” следует ложность суждения “Ни один человек не является способным к самосовершенствованию” (  |-
|- 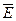 ).
).
2) Выводы из отношения противности.
Это отношение существует между суждениями I и О. Здесь возможны только выводы от ложности к истинности, поскольку эти суждения не могут быть вместе ложными, но могут быть вместе истинными. Это выводы:
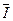 |-O,
|-O,  |-I.
|-I.
Пример.
Из ложности суждения “Некоторые люди подвержены лести” следует истинность суждения “Некоторые люди не подвержены лести” ( 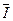 |-O).
|-O).
Пример.
Из ложности суждения “Некоторые люди не являются добрыми” следует истинность суждения “Некоторые люди являются добрыми” (  |-I).
|-I).
Пояснение. Конечно, последний вид выводов относительно тривиален. Дело в том, что из тех же посылок при помощи отношения противоречия могут быть сделаны более сильные заключения, выражаемые общими суждениями. Поэтому выводы, основанные на отношении противности, используются в естественном мышлении людей довольно редко.
3) Выводы из отношения противоречия.
Эти выводы также делятся на две группы: а) от ложности некоторого суждения к истинности другого" суждения и б) от истинности некоторого суждения к ложности другого суждения.
а) От ложности к истинности. Это выводы:
 |-O,
|-O,  |-A,
|-A, 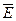 |-I,
|-I, 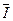 |-E.
|-E.
Пример.
Из ложности “Все люди имеют преступные наклонности” следует истинность суждения “Некоторые люди не имеют преступных наклонностей” (  |-O).
|-O).
|
|
|
Пример.
Из ложности “Некоторые люди не влияют на ход истории” следует истинность суждения “Все люди влияют на ход истории” (  |-A).
|-A).
Пример.
Из ложности “Ни один человек не имеет преступных наклонностей” следует истинность суждения “Некоторые люди не имеют преступных наклонностей”( 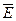 |-I).
|-I).
Пример< /I<.
Из ложности суждения “Некоторые люди заслуживают любви” следует истинность суждения “Ни один человек не заслуживает любви”( 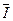 |-E).
|-E).
б) От истинности к ложности. Это выводы:
A|-  , O |-
, O |-  , E |-
, E |- 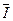 , I |-
, I |- 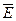 .
.
Пример.
Из истинности суждения “Некоторые великие люди не являются людьми низкого роста” следует ложность суждения “Все великие люди являются людьми низкого роста” (O |-  ).
).
Пример.
Из истинности суждения “Ни один лентяй не заслуживает похвалы” следует ложность суждения “Некоторые лентяи заслуживают похвалы”( E |- 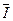 ).
).
Пример.
Из истинности суждения “Некоторые студенты получили пятерки по логике” следует ложность суждения “Ни один студент не получил пятерки по логике” (I |- 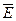 ).
).
4) Выводы из отношения противоположности.
Здесь возможны выводы только одного типа: от истинности к ложности, поскольку суждения, находящиеся в отношении противоположности не могут быть вместе истинными, но могут быть вместе ложными. Это выводы:
A|- 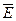 , E|-
, E|-  .
.
Пример.
Из истинности суждения “Все студенты являются находчивыми людьми” следует ложность суждения “Ни один студент не является находчивым человеком” (A|- 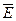 ).
).
Пример.
Из истинности суждения “Ни один по-настоящему добрый человек не ест мясо” следует ложность суждения “Все по-настоящему добрые люди едят мясо” (E|-  ).
).
Общее пояснение. Непосредственные умозаключения, включая и выводы по логическому квадрату, предназначены для того, чтобы полностью выявлять смысл категорического суждения и уметь по данному суждению строить другое сравнимое суждение, находящееся к нему в заданном отношении. Как мы уже видели, эти навыки чрезвычайно полезны в споре, когда очень быстро приходится анализировать смысл выдвигаемых суждений (тезисов) и находить суждения, подчиненные данным или находящиеся с ними в отношении противоречия.
|
|
|
§ 3. Простой категорический силлогизм
Логика исторически начиналась с силлогистики, т. е. теории силлогизмов. Автором этой теории был древнегреческий философ и ученый Аристотель. Мы знаем, что Аристотель был отцом логики. Главным его детищем и была силлогистика.
Чем важны силлогизмы для практики нашего мышления? Прежде всего тем, что рассуждения, из которых состоит значительная часть мышления и которые являются предметом логики, часто бывают длинными и запутанными. Поэтому их не всегда можно четко проанализировать сразу целиком. Отсюда возникает естественная мысль: нельзя ли их разбить на элементарные составляющие “кирпичики”, из которых построена значительная часть других рассуждений? Силлогизмы и представляют собой такие элементарные “кирпичики” значительного множества рассуждений. Если мы поймем, как строятся такие элементарные “кирпичики” и какие из них правильны, а затем разберемся в том, каким образом из этих “кирпичиков” строятся более сложные рассуждения, то мы получим в наше распоряжение хорошее средство анализа рассуждений и отличения правильных рассуждений от неправильных.
Что же такое простой категоричесиий силлогизм?
Простой категорический силлогизм - дедуктивное умозаключение, в котором из двух категорических суждений выводится новое категорическое суждение.
Мы видим, что силлогизм представляет собой последовательность суждений, в которой последнее суждение следует, выводится из предыдущих. Таким образом, силлогизм полностью подходит под наше понятие рассуждения. Особая важность силлогизмов для нашего мышления связана со статусом тех суждений, из которых составлены силлогизмы, а именно категорических ссждений. Категорические суждения предназначены для того, чтобы с максимальной ясностью и отчетливостью формулировать мысли, придавать нашим мыслям максимально определенную форму. Это, например, относится к тезисам в спорах и дискуссиях. Если же тезис в споре сформулирован в виде категорического суждения, то мы должны иметь в своем распоряжении логические средства, которые позволяют нам правильно и быстро преобразовывать категорические суждения. К такого рода средствам и относится простой категорический силлмгизм, который поможет нам овладеть запасом средств доказательства и опровержения категорических суждений, а значит, поможет достигать успеха в дискуссиях и вообще спорах.
|
|
|
Структура силлогизма
Рассмотрим простой пример простого категорического силлогизма
(1) Все люди разумны.
Все студенты - люди.
Следовательно, все студенты разумны.
Из чего состоит этот силлогизм? Сразу дадим определение:
Суждения, из которых выводится новое суждение, называются посылками силлогизма.
В нашем примере (1) это – суждениэ «Все люди разумны», «Все студенты – люди».
Суждение, которое выводится из посылок, назовем заключением силлогизма.
В нашем примере это – «Все студенты разумны».
“Следовательно” - это слово, обозначающее связку силлогизма. От всех других умозаключений силлогизм в данном случае отличается только тем, что в него входят суждения особого типа - категорические суждения, и что логическая связь между посылками и заключениями основывается именно на структуре категорических суждений.
Однако это заставляет нас более подробно проанализировать структуру силлогизма и рассмотреть не только суждения, из которых состоит силлогизм, но и те понятия, из которых состоят посылки и заключение.
Понятия, которые входят в посылки или заключение силлогизма, назовем терминами данного силлогизма.
В силлогизме обычно встречаются три термина.
Субъект заключения называется меньшим термином.
Предикат заключения называется большим термином.
Термин, который встречается в посылках, но не встречается в заключении, называется средним терминмм.
Пример. В приведенном ранее силлогизме “студенты” - меньший термин, “разумны” - больший термин, “люди” - средний термин.
|
|
|
В силлогизмах меньший термин обычно обозначается буквой S, больший термин - буквой P, а средний термин - буквой M.
Почему эти термины получили такое название легко увидеть, если изобразить отношение терминов приведенного выше силлогизма при помощи кругов Эйлера. Обозначим термин “студенты” через S, термин “люди” - через M, а термин “разумны” - через P. Тогда их отношение будет выглядерь следующим образом:

Рис. 1
Из диаграммы видно, что названия терминов соответствуют соотношению их объемов в некотором типичном силлогизме.
Особые названия имеют и посылки силлогизма.
Суждение, в которое входит больший термин, называется большей посылкой.
Суждение, в которое входит меньший термин, называется меньшей посылкой.
Традиционно в силлогизмах сначала указывается большая, а затем меньшая посылка. Например, мы не будем употреблять такую запись вышеприведенного силлогизма:
Все студенты - люди.
Все люди разумны.
Следовательно, все студенты разумны.
Если в силлогизме (1) заменить термины на их обозначения, то мы получим схему, по которой происходит вывод в данном силлогизме:
(1') Все M есть P.
Все S есть M.
 |
Все S есть P.
Здесь черта, как всегда, заменяет слово “следовательно”.
Эта схема напоминает нам примеры рассуждений, которые мы с вами рассматривали в самом начале нашего курса, когда вели речь об открытии Аристотеля, ставшем краеугольным камнем логики. Теперь мы можем сфмрмулировать это открытие Аристотеля точнее.
Содержание силлогизма - это понятия, встречающиеся в нем в качестве терминов.
Форма силлогизма - это связь, которая придается терминам.
Мы можем выделить форму силлогизма, заменив конкретные термины силлогизма на переменные типа S, M, P. Таким образом, приведенная выше схема (1') передает нам форму силлогизма (1).
Открытие Аристотеля в применении к силлогизмам звучит следующим образом:
Правильность силлогизма не зависит от его содержания, а зависит только от его формы.
В наших обычных рассуждениях мы привыкли иметь дело с истинными или принимаемыми за истинные суждениями, т. е. требуем, чтобы и посылки, и заключение правильного умозаключения были истинными. Это и есть то семантическое требование, которое логика предъявляет к правильным умозаключениям: при истинности посылок заключение должно быть истинным. Такая характеристика умозаключений сразу напоминает нам об отношении логического следования, которое мы рассматривали в главе 9. Таким образом, наше требование можно переформулировать следующим образом: между конъюнкцией посылок и заключением правильного силлогизма должно существовать отношение логического следования. Но мы помним, что отношение логического следования существует и если конъюнкция посылок ложна, а заключение истинно или также ложно. Это означает, что если мы в правильном силлогизме будем использовать ложные посылки, то правильность силлогизма от этого не изменится. Главное, чтобы не встречалось такого случая, чтобы конъюнкция посылок была истиннмй, а заключение - ложным. Правильность или неправильность силлогизма (как и любого другого дедуктивного умозаключения вообще не зависит от фактической истинности или ложности, входящих в него посылок. Например, следующее умозаключение является правильным, несмотря на то, что его посылки являются ложными:
|
|
|
Все республики несправедливы.
Все автократии - республики.
Следовательно, все автократии несправедливы.
Мы видим, что в этом умозаключении посылки ложны, заключение истинно, но тем не менее оно является правильным, так как если бы его посылки были истинными, то и заключение обязательно было бы истинным.
Показать это можно и следующим образом: если в данном умозаключении заменить термин “республики” на M, термин “несправедливы” - на P, термин “автократии” - на S, то мы получим уже знакомую нам схему:
Все M есть P.
Все S есть M.
Следовательно, все S есть P.
|
|
|


