 |
Аксиома силлогизма. Фигуры силлогизмов
|
|
|
|
Аксиома силлогизма
Мы уже с вами обсуждали тот тезис, что в силлогизме, как и в любом другом правильном дедуктивном умозаключении, имеется определенная принудительность: если посылки истинны, то нам ничего не остается, как признать истинность заключения, хотя бы это заключение и не было бы нам приятно. Откуда берется принудительный, необходимый характер силлогизмов?
В логике в качестве основания этого принудительного характера силлогизмов была сформулирована так называемая аксиома силлогизма, раскрывающая два главных типа отношений между терминами силлогизма, на которых основывается убедительная сила всех правильных силлогизмов.
Аксиома силлогизма: все, что утверждается относительно всего множества, утверждается и относительно каждого его подмножества, и все, что отрицается относительно всего множества, отрицается и относительно каждого его подмножества.
Аксиомой этот принцип называется потому, что он позволяет обосновать целый класс силлогизмов, к которым сводимы все остальные силлогизмы, и поэтому может считаться основанием всех вообще силлогизмов. В традиционной логике этот принцип получил название dictum de omni et nullo - речь обо всем и ни м чем.
С этим принципом связан другой принцип, имеющий латинское название nota notae - признак признака. Он выглядит следующим образом:
Признак признака есть признак самой вещи, а то, что отрицается относительно признака вещи, отрицается и относительно самой вещи.
Принцип nota notae также может служить основанием убедительной силы силлогизмов. Можно даже доказать, что эти два принципа равносильны, если принять следующее утверждение: объем понятия А есть часть объема понятия В, если и только если В есть признак А.
|
|
|
Dictum de omni et nullo формулируется для объемов терминов, входящих в силлогизм, а nota notae - для их содержаний.
Отсюда мы видим, что достоверность тех силлогизмов, которые были приведены ранее в этом параграфе, основывается на том, что термин P высказывается обо всем объеме термина M, а следовательно, в соответствии с принципом dictum de omni et nullo обо всяком подмножестве объема понятия M, а значит, и об S. В соответствии с отрицательной частью аксиомы силлогизма можно построить такой же убедительный силлогизм:
Ни один политик не может позволить себе быть до конца честным человеком.
Все депутаты - политики.
 |
Ни один депутат не может позволить себе быть до конца честным человеком.
Если в этом силлогизме термин “политик” обозначить через M, термин “до конца честный человек” - через P, термин “депутат” через S, то мы получим следующую схему:
Ни один M не есть P.
Все S есть M.
Следовательно, ни один S не есть P.
Здесь признак P отрицается относительно всего объема M, а следовательно, в соответствии с аксиомой силлогизма отрицается и относительно любого подмножества M, т. е. в том числе и S.

Рис. 2
Два разобранных типа силлогизмов являются наиболее употребительными и наиболее убедительными. Причины их убедительности мы уже рассмотрели, а причины употребительности рассмотрим несколько позже.
Для того, чтобы вести о силлогизмах более конкретный разговор, мы выделим определеные виды силлогизмов. Силлогизмы могут отличаться друг от друга, во-первых, составом суждений (как в приведенных выше примерах), и, во-вторых, расположением терминов. Сначала мы рассмотрим последнее различие.
Фигуры силлогизмов
Отличие в расположении терминов силлогизма можно свести к положению среднего термина в посылках, которое однозначно определяет положение всех остальных терминов.
|
|
|
Отсюда определение:
Фигурой силлогизма будем называть множество силлогизмов, характеризуемое одинаковым положением среднего термина.
Сколько возможно таких множеств силлогизмов? Для этого нужно ответить на вопрос: сколько раеличных положений может занимать в посылках силлогизма средний термин?
Во-первых, средний термин может быть субъектом большей посылки и предикатом меньшей.
Во-вторых, средний термин может быть предикатом в обеих посылках.
В-третьих, средний термин может быть субъектом в обеих посылках.
В-четвертых, средний термин может быть предикатом большей посылки и субъектом меньшей.
В соответствии с четырьмя видами положения среднего термина выделяются четыре фигуры силлогизмов, которые можно наглядно изобразить следующим образом (посылки изображаются горизонтальными отрезками, крайние точки отрезков обозначают термины, а наклонные или вертикальные линии соединяют средний термин в разных посылках):
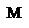
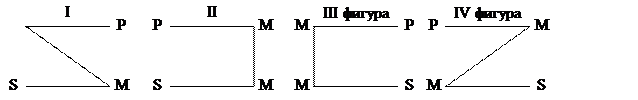
Рис. 3
Примеры силлогизмов по первой фигуре мы уже неоднократно встречали, поэтому приведем примеры силлогизмов по трем остальным фигурам:
Пример. Силлогизм по II фигуре[53]:
Ни один политик не стремится к истине ради нее самой.
Все настоящие ученые стремятся к истине ради нее самой.
Ни один настоящий ученый не является политиком.
Пример. Силлогизм по III фигуре:
Ни один страус не летает.
Все страусы птицы.
Некоторые птицы не летают.
Пример. Силлогизм по IV фигуре:
Ни один счастливый человек не стремится к справедливости.
Некоторые стремящиеся к справедливости люди являются юристами.
Некоторые юристы не являются счастливыми.
Логическое учение о фигурах силлогизма на первый взгляд может показаться чисто формальным, не имеющим отношения к реальным процессам рассуждений. Именно так его воспринимал, например, такой великий философ, как Иммануил Кант. Он даже написал специальную статью, которая называется “О ложном мудрствовании в четырех фигурах силлогизма”. Однако первое впечатление нас, как правило, обманывает. Существуют познавательные задачи, которые решают первые три фигуры силлогизма. Что касается четвертой, то по отношению к ней Кант, по-видимому, был прав. Она действительно не встречалась у автора силлогистики Аристотеля, который занимался логической теорией реальных рассуждений, а была добавлена, по-видимому, учениками Аристотеля Теофрастом и Евдемом, исходя из систематических соображений, как зеркально симметричная по отношению к первой фигуре.
|
|
|
Поэтому мы будем рассматривать следующий вопрос: какие познавательные задачи в ходе исследования или дискуссии можно решать при помощи силлогизмов?
1) Применение общих положений (аксиом, основоположений, законов природы, правовых норм) к частным случаям, или иначе говоря, подчинение частного общему.
Эту задачу решают силлогизмы по первой фигуре. Вы могли в этом убедиться на примерах силлогизмов, касающихся разумности людей, фемин, которые гантируются, и т. п. То же самое относится и к силлогизмам по первой фигуре с отрицательной посылкой.
Пример.
Ни одно конечное существо не может до конца понять замысел Творца.
Все люди - конечные существа.
Ни один человек не может до конца понять замысел Творца.
Мы подвели здесь множество людей под правило, говорящее о более широком множестве всех конечных существ.
2) Опровержение неправильных дедукций или неправильных подчинений.
Эта задача противоположна первой, и силлогизмы, решающие эту задачу, часто используются для опровержения выводов, сделанных по первой фигуре, если, конечно, они сделаны неправильно.
Пример. Представим себе судебный процесс. Обвинитель утверждает, что обвиняемый нанес смертельный удар. Как защитник должен доказывать, что это неверно? Например, так:
Этот смертельный удар нанесен человеком огромной силы.
Обвиняемый не является человеком огромной силы.
Обвиняемый не нанес этот смертельный удар.
Несложно заметить, что эро - силлогизм по второй фигуре.
Пример. Предположим, что нам надо опровергнуть суждение “Некоторые суеверные люди являются мужественными”.
|
|
|
Ни один мужественный человек не является боязливым.
Все суеверные люди боязливы.
Ни один суеверный человек не является мужественным.
3) Обоснование исключений из общих положений.
Эта ситуация часто встречается в споре. Предположим, Ваш оппонент выдвигает какое-либо общее положение, а Вам надо доказать исключение из него. Тогда можно смело прибегнуть к третьей фигуре силлогизма.
Пример. Предположим, нам надо доказать, что суждение “Все люди имеют преступные склонности” не является истинным. Тогда нам надо построить силлогизм по третьей фигуре:
Ни один ребенок не имеет преступных наклонностей.
Каждый ребенок является человеком.
Некоторые люди не имеют преступных наклонностей.
Таким образом, мы убедились, что различие фигур силлогизма не является чисто формальным. Строгое формальное разделение фигур имеет в своей основе различие задач, решаемых нами в практике аргументации.
|
|
|


