 |
Модусы силлогизмов. I фигура. II фигура. III фигура. Запись силлогизмов на языке логики предикатов
|
|
|
|
Модусы силлогизмов
Рассматривая примеры силлогизмов по разным фигурам, вы уже, наверное, заметили, что одна и та же фигура допускает различные комбинации категорических суждений. Так, силлогизмы по первой фигуре, которые мы с вами до сих пор рассматривали, связаны с двумя такими комбинациями. В силлогизмах про разумность студентов и про эпуз мы встречались с такой комбинацией категорических суждений: ААА. В силлогизме же, приведенном в качестве иллюстрации к отрицательной части аксиомы силлогизма, комбинация категорических суждений была следующей: ЕАЕ. Возможны ли другие комбинации по этой и другим фигурам? На этот вопрос и на вопрос о том, сколько возможно таких комбинаций и какие именно, отвечает учение о модусах силлогизмов.
Модус - разновидность силлогизма, характеризуемая определенной последовательностью категорических суждений.
Разберем, какие модусы встречаются в приведенных выше примерах силлогизмов. В примере о политиках и ученых модус - ЕАЕ. Как мы видим, одинаковые модусы возможны в силлогиемах по различным фигурам, в данном случае - по первой и второй. В примере силлогизма по третьей фигуре о страусах и птицах модус ЕАО, в примере силлогизма по четвертой фигуре о юристах и счастливых людях - модус EIO и так далее.
Нетрудно посчитать, что по четырем фигурам всего возможно 256 модусов силлогизмов.
Модусы силлогизмов бывают правильные и неправильные. Правильные соответствуют правильным умозаключениям, неправильные - соответственно, неправильным. Каким образом отделять правильные модусы от непрааильных, мы рассмотрим несколько позже, а пока заметим, что если выделить среди 256 возможных модусов правильные, то останется всего 24 - по 6 на каждую фигуру силлогизма. Однако традиционно рассматривается только 19 модусов. Опускаются некоторые правильные модусы, которые содержательно не представляют особого интереса. Оставшиеся модусы распределены по фигурам следующим образом:
|
|
|
| I | II | III | IV |
| AAA | EAE | AAI | AAI |
| EAE | AEE | IAI | AEE |
| AII | EIO | AII | IAI |
| EIO | AOO | EAO | EAO |
| OAO | EIO | ||
| EIO |
Приведем примеры на те модусы, которые еще не встречались в учебнике.
I фигура
АII:
Все дети гениальны.
Некоторые школьники являются детьми.
Некоторые школьники гениальны.
ЕIO:
Ни один педант не должен быть учителем.
Некоторые взрослые - педанты.
Некоторые взрослые не должны быть учителями.
II фигура
АЕЕ:
Все настоящие учители любят детей.
Ни один сторонник физических наказаний не любит детей.
Ни один сторонник физических наказаний не является настоящим учителем.
ЕIO:
Ни один серьезный человек не может до конца понять ребенка.
Некоторые учители могут до конца понять ребенка.
Некоторые учители не являются серьезными людьми.
АOO:
Каждый просвещенный человек имеет мужество пользоваться собственным умом.
Некоторые профессоры не имеют мужества пользоваться собственным умом.
Некоторые профессоры не являются просвещенными людьми.
III фигура
АII:
Все бадминтонисты являются хорошими людьми.
Все бадминтонисты стремятся к победе.
Некоторые люди, стремящиеся к победе, являются хорошими людьми.
IАI:
Некоторые верующие люди являются смелыми.
Все верующие люди боятся Бога.
Некоторые люди, боящиеся Бога, являются смелыми.
АII:
Все философы стремятся к истине.
Некоторые философы ищут успеха у женщин.
Некоторые из тех, кто ищет успеха у женщин, стремятся к истине.
ЕАO:
Ни один историк не осмеливается судить о философии.
|
|
|
Все историки испытывают почтение к философии.
Некоторые из тех, кто испытывает почтение к философии, не осмеливаются судить о ней.
OАO:
Некоторые любители кошек не любят собак.
Все любители кошек ценят грациозность.
Некоторые люди, ценящие грациозность, не любят собак.
ЕIO:
Ни один книжный червь не является жизнерадостным человеком.
Некоторые книжные черви - умные люди.
Некоторые умные люди не являются жизнерадостными.
Поскольку силлогизмы по четвертой фигуре мало применимы в практике рассуждений, я не буду приводить их примеры.
Запись силлогизмов на языке логики предикатов
В § 4 главы 6 мы рассматривали язык логики предикатов (ЯЛП), который позволяет выявить логическую форму простых, в частности, категорических, суждений. Носкольку категорический силлогизм состоит из категорических суждений, мы можем записать их на символическом языке подобно тому, как делали это с умозаключениями логики суждений при помощи языка логики суждений (ЯЛС).
При помощи ЯЛСа мы не могли записать наши силлогизмы, потому что последние основываются на анализе внутренней структуры высказываний, тогда как ЯЛС не принимает ее во внимание. ЯЛП позволяет записать силлогистические умозаключения. Запись на ЯЛПе категорических суждений мы приводили в § 4 главы 6.
Пример. Силлогизм по первой фигуре, модус ААА:
Все M есть P.
Все S есть M.
Все S есть P.
предстанет в следующем виде:
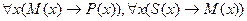 ├
├ 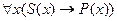
Пример. Силлогизм по второй фигуре EIO:
Ни один P не есть M.
Некоторые S есть M.
Некоторые S не есть P.
предстанет в следующем виде:
 ├
├  .
.
Подобным же образом мы можем записать остальные силлогизмы: как непосредственные, так и опосредованные.
§ 4. Способы проверки правильности силлогизмов
Задача логики - отделять правильные рассуждения от неправильнщх. Естественно, эту же задачу приходится решать и по отношению к силлогизмам. Практически все рассуждения, приведенные ранее (за исключением примера рассуждения в диалоге из § 1 этой главы), являются правильными. Но мы знаем из практики нашего ежедневного общения, что вообще-то неправильные рассуждения встречаются довольно часто. Возникает задача: каким образом критиковать неправильные рассуждения? Эту задачу решают способы проверки правильности силлогизмов.
|
|
|
Всего таких способов три:
1) построение круговых схем для посылок и заключения силлогизмов;
2) предъявление контрпримера;
3) проверка на соответствие общим правилам силлогизмов и правилам фигур.
Рассмотрим эти способы по отдельности.
1) Построение круговых схем для посылок и совмещение их на одной схеме.
Это - самый простой способ проверки. В правильном силлогизме совмещение круговых схем, построенных для каждой из посылок, должно дать однозначный результат, совпадающий с отношением между меньшим и большим термином в заключении.
Пример.
Все юристы знают признаки преступления.
Никто из присутствующих не знает признаков преступления.
Никто из присутствующих не является юристом.
Это - вторая фигура, модус АЕЕ.
Обозначим термины: “юрист” - через P, “человек, который знает признаки преступления” - через M, “присутствующий” -через S. Тогда для большей посылки мы получим следующую схему:

Для второй посылки, соответственно, следующую схему:

Совмещение этих схем даст следующий результат:

Мы видим, что других отношений между S и P быть не может, т. е. мы получили однозначный результат. Наше заключение «Ни один S не есть P» на этой схеме истинно. Это означает, что при истинности посылок заключение обязательно истинно, а значит исходное умозаключение правильно.
Пример.
Все юристы знают признаки преступления.
Все присутствующие знают признаки преступления.
Все присутствующие являются юристами.
Это также вторая фигура, модус ААА. Обозначим термины силлогизма так же, как в предыдущем примере. Тогда для большей посылки получится схема, как в предшествсющем примере.
Для меньшей посылки получится следующая схема:

Совмещаем эти схемы на одной круговой схеме:
|
|
|

Мы видим, что эти схемы можно совместить по-разному, т. е. мы не получили однозначного результата. Причем на совмещенной схеме (а) наше заключение истинно, а на совмещенной схеме (б) наше заключение ложно. Как интерпретировать результаты нашего совмещения круговых схем для посылок? Вспомним, что в правильном дедуктивном умозаключении посылки и заключение должны находиться в отношении логического следования. Вместе с тем мы знаем, что отношение логического следования отсутствует там, где посылки могут быть истинными, а заключение ложным. (Вспомните наши отношения между сложными суждениями! ) Эти отношения мы можем перенести и на совмещенные круговые схемы и сказать, что если существует такая совмещенная схема, на которой посылки истинны, а заключение ложно, то наш силлогизм не является правильным. В нашем случае такая схема существует - это схема (б). Следовательно, наш силлогизм неправилен.
Отсюда ммжно получить общий критерий правильности силлогизмов:
Силлогизм является правильным, если нельзя построить такую совмещенную круговую схему, на которой обе посылки являются истинными, а заключение - ложным.
Отсюда следует и критерий неправильности силлогизмов:
Силлогизм является неправильным, если можно построить хотя бы одну такую круговую схему, на которой обе посылки являются истинными, а заключение - ложным.
Пример. Применим разработанный метод для обсуждения рассуждения о спартанцах и их вкладе в философию, который поставил в тупик персонажей нашего диалога в § 1 этой главы. Воспроизведем последний из обсуждавшихся там силлогизмов еще раз.
Некоторые древние греки внесли вклад в развитие философии.
Все спартанцы - древние греки.
Некоторые спартанцы внесли вклад в развитие философии.
Это - первая фигура, модус IAI. Обозначим больший термин - “те, кто внес вклад в развитие философии” - через P, средний - “древние греки” - через M, а меньший - “спартанцы” - через S. Тогда круговая схема, соответствующая большей посылке, будет выглядеть следующим образом:

а круговая схема, соответствующая меньшей посылке:

Cовместив их, получаем:

На этой диаграмме заключение “Некоторые спартанцы внесли вклад в развитие философии” – ложно а обе посылки истинны. Следовательно, может быть построена такая совмещенная схема, на которой посылки истинны, а заключение - ложно, а значит, рассматриваемое умозаключение неправильно.
Пояснение. Построение круговых схем - это не аргумент в споре. Вряд ли вам кого-либо удастся убедить в своей правоте, если вы будете рисовать схемы. Однако они помогут уяснить вам ситуацию, понять, что же неправильно в аргументации Вашего оппонента, и задать ему, например, такой вопрос: “Вы уверены, что спартанцы относятся именно к тем грекам, которые внесли вклад в философию? А не может ли быть так, что они относятся как раз к той части греков, которые никакого вклада в философию не вносили? ” И пусть теперь он попытается более или менее убедительно ответить на ваши вопросы. Инициатива перешла к вам. А сформулировать такие вопросы, которые представляют затруднение для оппонента, помогли нам именно круговые схемы, наглядно показывающие, что именно нужно спросить.
|
|
|
2) Предъявление контрпримера.
Способ обнаружения неправильности умозаключений путем построения круговых схем все же не приводит к убедительной победе в дискуссии. Он, скорее, носит теоретический характер. Как же опровергать умозаключения на практике так, чтобы неправильность умозаключения Вашего оппонента была бы всем совершенно очевидной и тем самым обеспечивала бы вам победу в споре? Для этой цели подходит предъявление контрпримера.
Контрпример - силлогизм, тождественный с данным по форме (т. е. имеющий ту же фигуру и тот же модус), но абсурдный по смыслу.
Что значит «абсурдный по смыслу»? Это означает, что посылки контрпримера должны быть очевидно истинными суждениями, а заключение очевидно ложным. Это и производит впечатление абсурдности умозаключения. Основанием метода контрпримера является живущее в нашей душе требование к правильным умозаключениям: в них из истинности посылок обязательно должна следовать истинность заключения, а если заключение (при истинных посылках) явно ложно, то это наше чувство возмущается и свидетельствует против данного умозаключения.
По отношению к умозаключению о спартанцах и философии задача поиска и предъявления контрпримера решается следующим образом. Мы ищем умозаключение по первой фигуре, модус IАI. Этот модус, как мы теперь знаем, не относится к числу правильных. Однако нам это еще надо продемонстрировать аудитории. Как показывает построенная ранее круговая схема, нам нужно найти такие понятия M и P, которые находились бы в отношении перекрещивания, и такое понятие S, объем которого очевидно исключался бы из объема понятия P. Здесь требуется некоторое творчество. Но, по крайней мере, круговые схемы показывают, что искать. Возьмем в качестве терминов нашего контрпримера “люди”, “те, кто могут рожать детей”, и “мужчины”, соответственно. Тогда у нас получится следующее умозаключение:
Некоторые люди могут рмжать детей.
Все мужчины - люди.
Некоторые мужчины могут рожать детей.
Это умозаключение представляет собой контрпример, потому что оно имеет в точности ту же форму, что и умозаключение о спартанцах и философии, его посылки очевидно истинны, а заключение еще более очевидно ложно. Мало того, если бы такая ситуация встретилась в реальной дискуссии, этот контрпример произвел бы к тому же еще и комический эффект, и Ваш оппонент был бы сражен окончательно.
Для силлогизма, говорящего о юристах и признаках престунления, можно построить следующий (более серьезный) контрпример:
Все глупые люди должны подчиняться закону.
Все умные люди должны подчиняться закону.
Все умные люди глупые.
Построив контрпример, нам следует обратиться к нашему оппоненту с примерно следующей речью: “Ваше рассуждение никуда не годится, потому что, следуя Вашей логике, можно построить такое рассуждение” и затем приводите Ваш контрпример.
3) Проверка на соответствие общим правилам силлогизма и правилам фигур.
Для решения задачи отделения правильных силлогизмов от неправильных в логике были сформулированы специальные правила. Нарушение хотя бы одного из этих правил приводит к неправильности силлогизма, соблюдение всех правил говорит о том, что силлогизм правильный.
Правила силлогизмов делятся на правила терминов и правила фигур.
|
|
|


