 |
Корреляционно – регрессионный анализ зависимости результативного показателя от факторных показателей
|
|
|
|
Статистические распределения характеризуются наличием более или менее значительной вариации в величине признака у отдельных единиц совокупности.
Естественно, возникает вопрос о том, какие же причины формируют уровень признака в данной совокупности и каков конкретный вклад каждой из них. Изучение зависимости вариации признака от окружающих условий и составляет содержание теории корреляции.
Изучение действительности показывает, что вариация каждого изучаемого признака находится в тесной связи и взаимодействии с вариацией других признаков, характеризующих исследуемую совокупность единиц. В корреляционных связях между изменением факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных.
Корреляционно-регрессионный анализ проводится для определения степени связи между результатом и факторами, влияющими на результат.
Анализ влияния факторов на валовый надой на 1 корову, ц проводится по следующим данным: цена реализации молока, руб./ц– x1, и выручка на 100 га с/х угодий, тыс. руб - x2. Для начала необходимо определить характер связи между признаками и установить форму связи между ними.
Средние значения и изменение результативного и факторных признаков в совокупности в приложении № 2, приложении №3.
В результате решений уравнения на ЭВМ были получены следующие его параметры:
Y=4,79+0,03 *X1+0,08*X2
Интеграция полученных параметров следует:
A0=4,79 условное начало содержательной интерпретации не подлежит;
A1=0,03– коэффициент чистой регрессии при первом факторе свидетельствует о том, что при изменении цены реализации молока, руб./ц., валовый надой на 1 корову, ц. в среднем изменится на 0,03 ц. при условии, что другие факторы остаются постоянными;
|
|
|
A2=0,08- коэффициент чистой регрессии при втором факторе показывает, что при изменении выручки на 100 га с/х угодий, руб. вызывает изменение валового надоя на 1 корову, ц. при условии, что другие факторы остается постоянными.
Коэффициенты парной корреляции 0,70 свидетельствуют, что между валовым надоем на 1 корову, ц. и средней ценой реализации, руб/ц. существует связь средней силы и прямая зависимость, а 0,79- показывает, что связь сильная и прямая зависимость с выручкой на 100 га с/х угодий, тыс.руб.
Для сравнения коэффициентов регрессии выразим их в виде β - коэффициентах и коэффициентов эластичности.
β – коэффициенты показывают, что если величина фактора изменяется на одно среднеквадратическое отклонение, результативный признак увеличится (уменьшится) на величину β – коэффициента своего квадратического отклонения, при постоянстве остальных факторов.
Коэффициенты эластичности показывают, что если величина факторного признака увеличится на 1%, результативный признак увеличится (уменьшится) соответственно на коэффициент эластичности, выраженный в % при постоянстве других факторов.
Рассчитаем среднее значение признака и определим среднеквадратическое отклонение.
ỹ=∑y/n (2.4)
где, ỹ- среднее значение результативного признака;
∑y- сумма результативного признака по всем районам;
n- число районов (23).
ỹ=31,47
1=∑ X1/n (2.5)
где, X1- среднее значение первого факторного признака;
∑ X1- сумма первого факторного признака по всем районам;
n- число районов (23).
X1=655,70
X2=∑ X2/n, где
X2- среднее значение второго факторного признака;
|
|
|
∑ X2- сумма второго факторного признака по всем районам;
n- число районов (23).
X2=63,37
бy=(∑(yi-y)2/n)1/2; бy=2428,75 (2.5)
бх1=(∑(xi1-x1)2/n)1/2;бх1=167776,87 (2.6)
бх2=(∑(xi2-x1)2/n)1/2;бх2=139984,85 (2.7)
Теперь можно определить β - коэффициенты и коэффициенты эластичности.
β1=0,03*бх1/бy;β1=0,03*167776,87/2428,75=2,07 (2.8)
β2=0,08*бх2/бy;β2=0,08*139984,85/2428,75=4,61 (2.9)
Сопоставление β – коэффициентов показывает, что наиболее сильное влияние на варьирование результативного фактора оказывает выручка на 100 га с/х угодий, тыс.руб., менее сильное воздействии – цена реализации молока, руб./ц.
Э1=а1* X1/ ỹ; Э1=0,03*655,70/31,47=0,63% (2.10)
Э2=а2* X2/ ỹ; Э2=0,08*63,37/31,47=0,16 % (2.11)
Первый коэффициент эластичности показывает, что при изменении цены реализации молока, руб./ц. на 1% валовый надой на 1 корову, ц. изменится на 0,63%. Второй коэффициент эластичности показывает, что при изменении выручки на 100 га с/х угодий, тыс.руб. на 1% валовый надой на 1 корову, ц. изменится на 0,16%.
Таким образом, из анализа видно, что на валовый надой на 1 корову, ц влияет и цена реализации молока, руб/ц, и выручка на 100 га с/х угодий, тыс.руб. примерно одинаково.
Коэффициент множественной корреляции равен 0,81, он говорит о том, что связь сильная (приложение №3). Также был рассчитан коэффициент детерминации, который является квадратом коэффициент корреляции. Он показывает, насколько тесной является связь между выбранными показателями. В нашем случае он равен 0,65, т.е. связь между признаками средняя.
Проверка значимости коэффициента множественной корреляции показала, что F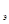 
= 18,98, при значимости Fтабл. =3,42 при пятипроцентном уровне. Таким образом, F 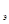> Fтабл, что позволяет с вероятностью 95 % утверждать существенность различий в величине дисперсий и соответственно сделать вывод об адекватности модели.
В качестве критериев проверки гипотез относительно двух средних используется критерий t- Стьюдента. Фактическое значение t равно 0,35;
|
|
|
1,48;3,15, а табличное t=2,07, необходимо признать справедливость альтернативной гипотезы.
|
|
|
