Алгоритм Форда-Фалкерсона для нахождения максимального потока в сети

 

Алгоритм решения задач нахождения максимального потока в железнодорожной сети основан на теореме Форда-Фалкерсона: в любой транспортной сети максимальный поток равен минимальной пропускной способности. Если поток максимален, то найдется такое сечение, пропускная способность которого равна мощности потока. Доказывается эта теорема применением алгоритма Форд-Фалкерсона. Согласно этому алгоритму, начиная с некоторого начального неполного потока, по итеративному алгоритму можно получить полный поток, если прибавлять к различным значениям потоков  пути  минимальное из чисел 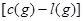, которые вычислены по этому пути. После такой операции путь  уже будет содержать хотя бы одну ненасыщенную дугу. Если таким же образом поступить с другими путями , то, в конце концов, получим полный поток. Поэтому алгоритм определения максимального потока состоит из следующих шагов:

Строим начальный поток ;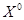

проверяем, попал ли узел  в множество узлов , которые достижимы по ненасыщенным ребрам из . Если узел  не попал, то считают, что построенный поток максимален, и алгоритм расчета останавливается;

если узел  попал во множество , то выделяют путь , состоящий из ненасыщенных ребер и ведущий грузы из  в ;

увеличивают поток через каждое ребро этого пути на величину ;

строят новый поток  и переходят к шагу 2.

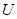Обычно сеть задается матрицей пропускной способностей  всех ребер сети . Задавая , затем вычисляют на k-м шаге матрицу значений потоков на дугах . Строят матрицу разностей . В этой матрице насыщенным ребрам при потоке  будут соответствовать нулевые элементы, ненасыщенным - ненулевые элементы. Поэтому вычисление матрицы  достаточно как для построения множества узлов по которым вещество из  достигает по ненасыщенным ребрам до , так и для построения последовательности ненасыщенных ребер.

Технология составления этих списков следующая:

сначала составляют список узлов, в каждый из которых ведет ненасыщенное ребро из вершины i;

далее для каждого i-го узла составляют свой список узлов, в каждый из которых из i-го узла ведет ненасыщенное ребро (за исключением тех узлов, которые уже вошли в ранее составленные списки) и так далее.

Этот процесс выписывания списков заканчивается в двух случаев. Либо появиться узел 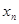, что означает продолжение работы алгоритма, либо в список выписанных узлов не попал узел 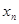, что означает конец расчетов.

 

Метод Монте-Карло

 

Пусть требуется разыграть дискретную случайную величину X, т. е получить последовательность её возможных значений x_i, зная закон распределения X:

 

X	x1	x2	…	xn
p	p1	p2	…	pn

Рисунок 1.1 - Распределение случайной величины X

 

Обозначим через R непрерывную случайную величину, распределённую равномерно в интервале (0,1), а через r_j,  - её возможные значения, т.е. случайные числа.

Разобьём интервал 0£ R <1 на оси Оr точками с координатами p₁, p₁+ p_2, p₁+ p₂+ p_3,..., p₁ + p₂ +…+ p_n-1 на n частичных интервалов ∆₁, ∆_2,..., ∆_n, длины которых p_1, p₂,…, p_n соответственно. Таким образом, |∆_i|= p_{i (}1), где i=1, 2, …,n.

Теорема: если каждому случайному числу r_j (0£ r_j <1), которое попало в интервал ∆_i, ставить в соответствие возможное значение x_i, то разыгрываемая величина будет иметь заданный закон распределения:

Так как при попадании случайного числа r_j в частичный интервал ∆_i разыгрываемая величина принимает возможное значение x_i, а таких интервалов всего n, то разыгрываемая величина имеет те же возможные значения, что и X, а именно x_1, x_2,..., x_n. Вероятность попадания случайной величины R в интервал ∆_i равна его длине, а в силу |∆_i|= p_i, получим, что вероятность попадания R в интервал ∆_i равна p_i. Следовательно, вероятность того, что разыгрываемая величина примет возможное значение x_i, также равна p_i. Таким образом разыгрываемая величина имеет заданный закон распределения как показано на рисунке 1.1

Правило: для того чтобы разыграть дискретную случайную величину, заданную законом распределения (2) нужно:

1) разбить интервал (0;

2) оси на Or на n частичных интервалов:

 

∆₁ = (0; p₁), ∆₂= (p₁; p₁ +p₂),..., ∆_n= (p₁ +p₂ +…+p_n-1;

 

3) выбрать случайное число r_{j (}например, из таблицы случайных чисел). Если r_j попало в частичный интервал ∆_i, то разыгрываемая случайная величина приняла возможное значение x_i.

12345

Поделиться:

Воспользуйтесь поиском по сайту: