Предел функции в бесконечности и в точке

Рис.6.2

Итак, число А есть предел числовой последовательности {а„}, если

для любого е>0 найдется номер N, начиная с которого (при n>N) все члены последовательности будут заключены в е-окрестности точки А, какой бы узкой она ни была. Вне этой е-окрестности может бьпъ лишь конечное число членов данной последовательности.

Предел функции в бесконечности и в точке

Предел функции в бесконечности. С понятием предела число­вой последовательности а„ ⁼Ди) тесно связано понятие предела функции у= fix) в бесконечности. Если в первом случае пере­менная я, возрастая, принимает лишь целые значения, то во вто­ром случае переменная х, изменяясь, принимает любые значения.

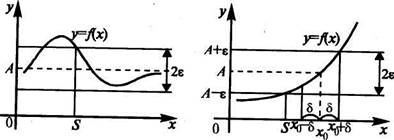
Определение. Число А называется пределом функции y=f(x) при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа е>0, найдется такое положи­тельное число S >0 {зависящее от е; S=S(e)), что для всех х таких, что I х I >S, верно неравенство:

 

(6.3)

\fix)-A\<s.

Этот предел функции обозначается lim f(x) = А или Дх)-»/4 при х-х».

С помощью логических символов определение имеет вид:

(а = lim Дх)1 о (V* > 0)(35 = S(e) > 0)(Vx:|x| > S)\fix)-A\ <е.

А+г

А-г

Смысл определения остается тем же, что для предела числовой последовательности: при достаточно больших по модулю значе­ниях х значения функции fix) как угодно мало отличаются от числа А (по абсолютной величине).

Рис.6.4

Рис. 6.3

Выясним геометрический смысл предела функ­ции у= fix) в бесконечности. Неравенство (6.3) \fix)—A\<e равно­сильно двойному неравенству A~E<fix)< А+г, соответствующему расположению части графика в полосе шириной 2е (см. рис. 6.3).

Итак, число А есть предел функции у= fix) при х-хю, если для любого б>0 найдется такое число <S>0, что для всех х таких, что I х | >S, соответствующие ординаты графика функции fix) будут заключены в полосе А—Е<у<А+в, какой бы узкрй эта полоса ни была.

ОПрнмер 6.2. Доказать, что

*->» X

5л:+ 1

<8

-5

Решение. Для любого е>0 неравенство (6.3)

1. | i.l

или т-т <в выполняется при I х \ > —.

И ⁸

Итак, для любого е>0 существует такое число S= — >0, что для

е

всех х, таких, что I х| >S, будет верно неравенство |Дх)—5 | <е, где

_,_v __r; а это и означает, что lim /(x)=5>-

X Х->оо

Замечание. Приведенное выше определение предела при х-х» предполагает неограниченное возрастание независимой пере­менной х по абсолютной величине. В то же время можно сформули­ровать понятие предела при стремлении х к бесконечности оп­ределенного знака, т.е. при х -> +оо и при х ->• —«. В первом случае основное неравенство (6.3) должно выполняться для всех х таких, что х > S, а во втором — для всех х таких, что х <— S.

Предел функции в точке. Пусть функция y=fix) задана в неко­торой окрестности точки х₀, кроме, быть может, самой точки х₀.

Определение. Число А называется пределом функции fix) при х, стремящемся к xq (или в точке xq), если для любого, даже сколь угодно малого положительного числа е>0, найдется такое положи­тельное число 8>0 (зависящее от е, 8=8(8)), что для всех х, не рав­ных х₀ и удовлетворяющих условию

1х^х_о|<5, (6.4)

выполняется неравенство

\fix)-A\<s. (6.5)

Этот предел функции обозначается lim f(x)= А или fix)^A

прих-*х₀.

С помощью логических символов определение имеет вид:

[ А = lim /(х)] о (Ve > 0)(36 = 5(б) > 0)(Vx * х₀: |х - х_о| < 6)

\fix)-A\<e.

Смысл определения предела функции fix) в точке х₀ состоит в том, что для всех значений х, достаточно близких к х₀, значения функции fix) как угодно мало отличаются от числа А (по абсо­лютной величине).

Рассмотрим геометрический смысл предела функции в точке. Как отмечалось выше, неравенство \fix)—A\<s равносильно двойному неравенству A~R<fix)<A+e, соответствую­щему расположению части графика в полосе шириной 2е (см. рис.6.4.). Аналогично неравенство 1х—х₀ |<8 равносильно двой-

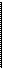ному неравенству х₀ -8<х< х₀ +8, соответствующему попаданию точек х в 5-окрестность точки х₀.

Число А есть предел функции fix) при х-»х₀, если для любого s>0 найдется такая Ъ-окрестность точки х₀, что для всех х *х₀ из

этой окрестности соответствующие ординаты графика функции
Дх) будут заключены в полосе А—Е<у<А+г, какой бы узкой эта
полоса ни была. Щ

ОПример 6.3. Доказать, что Шп(2х + 3) =5. 1

1 Щ

Решение. Пусть е=0,1. Тогда неравенство (6.5) |(2х+3)— —51 <0,1 будет выполняться при Ix—1|<0,05. Аналогично при е=0,01 то же неравенство (6.5) будет верно при |х—11 <0,005.

Для любого е>0 неравенство (6.5) I (2х+3)—51 <е будет выпол-

няться при I х— 11 < —.

Итак, при любом е>0 существует такое число 8= —(для е=0,1

8=0,05; для е=0,01 8=0,005 и т.д.), что для всех х*1 и удовлетво* ряющих условию! лг—11 <S верно неравенство 1Дх)—51 <е, гдв Дх)=2х+3; а это и означает, что lim f(x) =5.^

х->1 i

Замечание 1. Определение предела не требует существо-, вания функции в самой точке х₀, ибо рассматривает значения в некоторой окрестности точки х₀. Другими словами, рас-

сматривая lim f(x), мы предполагаем, что х стремится к x_Q, но

X->XQ

не достигает значения х₀. Поэтому наличие или отсутствие пре­дела при х->х₀ определяется поведением функции в окрестности точки х₀, но не связано со значением функции (или его отсутст­вием) в самой точке jc₀.

Замечание 2. Если при стремлении х к х₀ переменная х принимает лишь значения, меньшие х₀, или наоборот, лишь значен! ния, большие х₀, и при этом функция fix) стремится к некоторому^, числу А, то говорят об односторонних пределах функции Дх) соответ­ственно слева lim f(x) и справа lim Дх) = А. Очевидно, что

j(+0

определение этих пределов будет аналогично рассмотренному выше

при х-»х₀, если вместо значений х, удовлетворяющих условию (6.4), при которых верно неравенство (6.5), рассматривать значения х та­кие, что х₀ —8<х< х₀ при х->х₀ -0 (слева), или значения х такие, что х₀ <х< х₀ +8 при х-»х₀ +0 (справа).

Разумеется, если lim /(x)= lim /(х)=Я, то lim f{x)=A.

Бесконечно малые величины

Определение. Функция а(х) называется бесконечно малой вели- ' чиной при х->лг<), или при х-юо, если ее предел равен нулю:

lim а(х) =0.

Х->Х₀(со)

Зная определение предела функции при х->х₀ и при х-х», мож­но дать развернутое определение бесконечно малой величины:

Функция а(х) называется бесконечно малой величиной при х->щ, если для любого, даже сколь угодно малого положительного числа е>0, найдется такое положительное число 8>0 (зависящее от s, д=Б(е)), что для всехх, не равных х₀ и удовлетворяющих условию

1х-х_о|<5,, (6.6)

будет верно неравенство

I а(х) I <8. (6.7)

С помощью логических символов приведем это определение к виду:

• (Ve>0)(38=8(e)>0)(Vx* х0: |х - хо|

а(х) - бесконечно

малая при х -> х₀

при lim a(x) = 0 х-*х₀

Аналогично можно сформулировать определение бесконечно малой при х-*», если основное неравенство (6.7) рассматривать для достаточно больших х. Приводим его в краткой форме:

4?(e)>0)(Vx: \x\>S)

а(х) - бесконечно

малая при х -> при lim а(х) = 0

 

При Х-»оо

Например, функции y=cos х при х-> — и у=---------------

2 2х - 7

есть бесконечно малые величины, ибо их пределы равны нулю. ^
Не следует путать бесконечно малую переменную величину а(х) с [
очень малым, но постоянным числом е>0, ибо по мере приближения? |
.значений х к х₀ (при х-»х₀) или по мере увеличения по модулю, |
значений х (при х-х») функция a(jc) в соответствии с (6.7) окажется¹
меньше этого числа s (по абсолютной величине). '

Связь бесконечно малых величин с пределами функций. Теоре­ма. Если функция Дх) имеет при х-*х₀ (х->оо) предел, равный А, то \

ее можно представить в виде суммы этого числа А и бесконечно малой а(х) при х-> х₀ (х-»оо)

Дх)=Л+а(х). (6.8)

□ Докажем теорему для случая х->х₀ ¹. По условию lim f(x) =

хх

=А. Это означает, что для любого s>0 существует такое число
8>0, что для всех х * х₀ и удовлетворяющих условию I х— х₀ | <8^
будет верно неравенство 1Дх)— А\<е, или, обозначив ос(х)= Дх)-Л,
справедливо неравенство I а(х) | <е. Это и означает, что а(х) есть
бесконечно малая при х-»х₀.■ '

Верна и обратная теорема:

Теорема. Если функцию Дх) можно представить как сумму числа А и бесконечно малой а(х) при х-»х₀ (х-кю), то число А есть предел

этой функции при х->х₀ (х->оо), т.е. lim f(x)=A.

П По условию Дх)=Л+а(х). Пусть, например, х->х₀.

Так как функция а(х)=Дх)— А есть бесконечно малая при х->х₀, то для любого числа в>0 существует такое число 8>0, что

для всех х *х₀ и удовлетворяющих условию I х-х₀ I <8 верно не­равенство I а(х) | =| Дх)— А | <е.

Это и означает, что lim /(х) =А.«а* Ш

Свойства бесконечно малых величин:

1. Алгебраическая сумма конечного числа бесконечно малых вели­
чин есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную
функцию (в том числе на постоянную, на другую бесконечно ма­
лую) есть величина бесконечно малая.

3. Частное от деления бесконечно малой величины на функцию,
предел которой отличен от нуля, есть величина бесконечно малая.

□ В качестве примера докажем свойство 1 для двух бесконечно малых а(х) и р(х) при х-»х₀. Покажем, что функция (а(х)+р(х)) также является бесконечно малой при х-> х₀.

По условию а(х) и р(х) есть бесконечно малые при х->х₀.

Это означает, что для любого е' =—>0 найдутся такие числа

2), 5₂>0, что для всех х *х₀ и удовлетворяющих условиям

|х-х0 и |х-х0 |<82. выполняются соответственно неравенства

(6.9) (6.10)

(6.11)

и

Е

(6.12)

Если взять в качестве числа 8 минимальное из чисел 81И82, т.е. 5=min{8₁,8₂}, то неравенству \х—х₀ |<5 будут удовлетворять решения обоих неравенств (6.9) и (6.10), а следовательно, одно­временно будут верны неравенства (6.11) и (6.12). Складывая почленно неравенства (6.11) и (6.12), получим, что

 

¹ Здесь и далее доказательство основных сюйств бесконечно малых и бесконечно боль­ших величин, пределов функций проводим для случая х -* xq, рассматривая поведение

функции в некоторой окрестности точки до. т.е. для х е (х₀ - 8, х₀ + б), где §>0. Дока­зательство тех же утверждений для случая х ->•«: полностью идентично, если рассматри­вать поведение функции при достаточно больших (по модулю) значениях х, т.е. при | х |

>5(ще5>0)илипри хе(-=о;-5)и(^; + °°).

Используя свойство абсолютных величин (см. §5.2), т.е. |а(х)+р(х) | < I a(x) I +1 р(х) |, придем к более сильному неравенству

I <Х(Х)+Р(Х) | < Б. (6.13)

 

> - или I Дх) | >М, где Дх)= —— и М= -. А это и означает,

\. Произведение бесконечно большой величины на функцию, пре­дел которой отличен от нуля, есть величина бесконечно большая.

2. Сумма бесконечно большой величины и ограниченной функции
есть величина бесконечно большая.

3. Частное от деления бесконечно большой величины на функцию,
имеющую предел, есть величина бесконечно большая.

Например, если функция Дх)= tgx есть бесконечно большая

величина при х-> — (ибо lim /(х) =00), функция ф(х)=4х— 3 при
² "I

х~> — имеет предел (2л—3), отличный от нуля, а функция у(х)=

=sinx — ограниченная функция, то функции Дх)ф(х)=(4х—3) tgx

fix) (по свойству 1), J{x)+\]i(x)=tg x+sinx (по свойству 2),

tgx 4х-3

Ф(х) (по свойству 3) являются бесконечно большими величи-

что

а(х)

А(х)

при х-»х₀ функция Дх) является бесконечно большой. Доказательство второго утверждения аналогично.И

Например, если функции >»=cos х при х-л — и у= при х-к»

L ZX — 7

есть величины бесконечно малые, то функции у=---- при х->—,

cos х 2.

2х - 7
у=------- при х-*ю есть бесконечно величины большие. И наоборот,

если функции y=tg х при х-> —, y=-j5x - 7 при х->оо есть величины

бесконечно большие, то функции у =------- =ctg x при х->— и

tgx 2

у= _u == при х-*оо есть величины бесконечно малые.

 

нами при х-> ^-.

Связь между бесконечно малыми и бесконечно большими вели­
чинами. Теорема. Если функция а(х) есть бесконечно малая величи­
на при х-»х_о(х-*»), то функция Дх)~--------- является бесконечно

а(х) большой при х-»Хо(х-*)о). И обратно, если функция Дх) бесконечно

большая при х-> х₀ (х-хх>), то функция Дх)=- есть величина бес- >

а(х)

конечно малая при х-»х₀

П Докажем первое утверждение для случая x->Xq, т.е. если а(х) — Ц

бесконечно малая, тоДх)= ——есть бесконечно большая при х-»х₀.

а(х)

По условию а(х) — бесконечно малая при х->х₀, следовательно, для любого е>0 найдется такое 5>0, что для всех х^х_ои удовлетво­ряющих условию I х— х₀1 <5 будет верно неравенство | а(х) | <е. По­следнее неравенство (в предположении, что в некоторой окрестно­сти точки х₀ при х*х₀ а(х);*0) равносильно следующему

123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: