Общая схема исследования функций и построения их графиков

При исследовании функций и построении их графиков реко­мендуется использовать следующую схему:

1°. Найти область определения функции.

2°. Исследовать функцию на четность—нечетность.

3°. Найти вертикальные асимптоты.

4°. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.

5°. Найти экстремумы и интервалы монотонности функции.

6°. Найти интервалы выпуклости функции и точки перегиба.

7°. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.

Заметим, что исследование функции проводится одновремен­но с построением ее графика.

1 + х²

ОПример 8.13. Исследовать функцию у=------ =- и построить

1-х²

ее график.

Решение. 1°. Область определения (—оо, — 1)U(~ I, 1)U U(l,+oo), т.е. х*±1.

2°. Функция четная, так как f(—x) =f(x), и ее график симмет­ричен относительно оси ординат.

3°. Вертикальные асимптоты могут пересекать ось абсцисс в точках х = ±1. Так как пределы функции при х-» 1—0 (слева) и при х->1+0 (справа) бесконечны, т.е.

-=—oo и lim

lim

=+оо, то прямая х=1 есть верти-

кальная асимптота. В силу симметрии графика /(х) х = — 1 также вертикальная асимптота.

у=—\ — горизонтальная асимптота.

5°. Экстремумы и интервалы монотонности.

у'~0 при х=0

, 2х(1-х²)-(1 + х²)(-2х) 4х
Найдем у '= —------- ' \, ^v— -

(1-х²)² (1-х²)²

и у' не существует при х = ±1.

Однако критической является только точка x_Y = 0 (так как

значения х = ±1 не входят в область определения функции). По­
скольку при х< 0 /'(х)<0, а при х>0 /'(х)>0 (рис.8.21), то х=0 —
точка минимума и

-1>* 0 ^* 1 Рис. 8.21

^, /min⁼⁼/°)⁼¹ — МИНИМУМ

х функции. На интервалах (—оо,—1) и (—1, 0) функция убывает, на интервалах (О, 1) и (1, оо) — возрастает.

6°. Интервалы выпуклости и точки перегиба. Найдем

„_ 4(1 - х²)² - 4х • 2(1 - х²)(-2х) _ 4(1 + Зх²)
^У (1-х²)⁴ (1-х²)³

Очевидно, что у">0 на интервале (—1, 1) и функция выпукла вниз на этом интервале. у"<0 на интервалах (—оо,—1), (1, оо), и на

-1	\	У
	|_ -1	j	1 "х

этих интервалах функция выпукла вверх. Точек пере­гиба нет.

7°. Точки пересечения с осями. /(0)=1, т.е. точка пере­сечения с осью ординат (0, 1). Уравнение /(х)=0 решений не имеет, следовательно, график функции не пересекает ось абсцисс.

Рис. 8.22

График функции изобра-

 

Пример 8.14. Исследовать функцию у=2хе ² и построить ее график.

Решение. 1°. Область определения (—да, оо).

2°. Функция нечетная, так как Д— х)=— Дх) и график ее сим­метричен относительно начала координат.

3°. Вертикальных асимптот нет, так как функция определена при всех действительных значениях х.

4°. Поведение функции в бесконечности:

hm f(x)~ hm ——j- == — = lim ------- -= lim --- т~®-

X-»+cc X—»+oo X L^J ^X~ ^>+0° (^x^\ X—» + oo X

<?^T \e~\ xi^

В силу нечетности функции lim /(jc)=O, т.е. прямая у=0

Х->-оо

(ось абсцисс) — горизонтальная асимптота. 5°. Экстремумы и интервалы монотонности:

if if! zi.

у'=2е ² +2хе ² (-х) = 2е ² (1-х²);

у' = 0 при х = ±1, т.е. критические точки х±=— 1, х= 1. Знаки производной изображены на рис. 8.23.

Таким образом, х=—1 есть точка минимума; х=1 — точка мак­симума и

_^ /min ⁼-Д~ 1)⁼~~ ~7= ^Ю~Ь21,

-1

тервалах (->/з~, 0) и (V?, °°) и выпукла вверх на интервалах (—оо, J и (0, -Jb), а Ху——-^, jc₂ = V^ — точки перегиба.

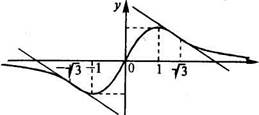7°. Д0)=0. Уравнение. Дх)=0 имеет единствен­ное решение х=0, т.е. график функции пере- х секает оси в начале координат (0; 0). График функции изо-

Рис. 8.25 бражен на рис. 8.25.^

Решение задач

О Пример 8.15. Найти пределы:

a) li

; б) li

1-JC

Р е ш е н и е. а) Имеем неопределенность вида [оо—оо]. Вынося

/1 + х1, придем к неопределенности вида | —

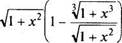
lim (Vl + х2 - л/l + х3) =[00-00]= lim

О

 

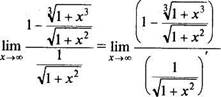
Рис. 8.23

Функция убывает на интервалах (-да,—1) и (—1, да) и возраста­ет на интервале (—1, 1).

6°. Интервалы выпуклости и точки перегиба:

-> л -х²

у"=2е² {-х){\-х²) + 2е ² = ~2хе 2 (3-х2); у "=0 при х=0 и х= ±>р. Знаки второй производной изображены на рис. 8.24.

У" — ^Z^+^V^— ^ f "т~ ^ Таким образом, функ- у f\ --/I \J 0 Г\~Р V/ х ция выпукла вниз на ин- Рис. 8.24

 

= lim

\\ + х² _^г0
1 О

Vl + x² Далее применим правило Лопиталя:

Глава 9. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 9.1. Понятие дифференциала функции

Пусть функция y=f{x) определена на промежутке X и диффе­ренцируема в некоторой окрестности точки хеХ. Тогда существу­ет конечная производная

lira -^ =/'(*)• д*-*0 Ах

На основании теоремы о связи бесконечно малых величин с пределами функций можно записать

/(х) Ах

где а(Лх) — бесконечно малая величина при Лх-»0, откуда

Ay=f'(x)Ax +а(Дх)Ах. (9.1)

Таким образом, приращение функции Ау состоит из двух сла­гаемых: 1) линейного относительно Ах; 2) нелинейного (представ­ляющего бесконечно малую более высокого порядка, чем Ах, ибо

а (Ах) Ах

(см. замечание в § 6.3) lim---------- = lim <х(Дх) =0).

Лх-»0 Дх Дх-»0

Определение. Дифференциалом функции называется главная, линейная относительно Ах часть приращения функции, равная про­изведению производной на приращение независимой переменной

dy=f'(x)Ax. (9.2)

|>Пример 9.1. Найти приращение и дифференциал функции

у=2х² - Зхпри х=10 и Ах=0,1.

Решение. Приращение функции

4У = Л* + Ах) -Л*) = [2(jc + Ах)² - 3(х + Ах)] = Дх(4х + 2Дх -3).

Дифференциал функции dy=f'(x)Ax=(4x— 3)Дх.

При х=10 и Ах=0,1 имеем Aj>=3,72 и dy=3,70. Различие между Ау и dy составляет всего 0,02, или 0,5%>-

D Пример 9.2. Найти дифференциал функции у=х. Решение. dy=dx=x'-Ax, откуда

ах=Ах,

т.е. дифференциал независимой переменной равен приращению этой переменной.^-

Поэтому формулу для дифференцирования функции можно записать в виде

dy=f'(x) ах, (9.3)

откуда/'(х)= —. Теперь ъил видим, что —не просто символиче-
dx ax

У, i

ское обозначение производной, а обычная дробь с числителем dy и знаменателем ах.

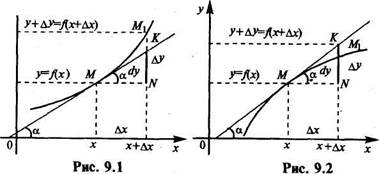
Геометрический смысл дифференциала. Возьмем на графике функции у=Лх) произвольную точку М(х, у). Дадим аргументу х приращение Ах. Тогда функция у = Дх) получит приращение 4У=Дх+ Ах)-Дх) (см.рис. 9.1)

Проведем касательную к кривой у = Дх) в точке М, которая образует угол а с положительным направлением ори Ох, т.е. fix) =tg а. Из прямоугольного треугольника MKN

KN=MN-tg ос=Дх tg ос=/'(х)Дх,

т.е. в соответствии с (9.2) dy=KN.

Таким образом, дифференциал функции есть приращение орди­наты касательной, проведенной к графику функции у=Лх) в данной точке, когда х получает приращение Ах.

Не следует думать, что всегда dy<Ay. Так, на рис. 9.2 показан случай, когда dy>Ay.

 

 

Свойства дифференциала. Свойства дифференциала в основ­ном аналогичны свойствам производной. Приведем их без дока­зательства:

1. dc=0. 4. d(uv)=v du+u dv.

2. d(cu)=c du.

_ ,{u) vdu-udv
5. d\-\ =------ j----

3. d(u±v)=du±dv.

Остановимся теперь на важном свойстве, которым обладает дифференциал функции, но не обладает ее производная.

Инвариантность формы дифференциала. Рассматривая выше У⁼Л^Х) ^как функцию независимой переменной х, мы получили, что dy=f'{x)dx. Рассмотрим функцию y=flu), где аргумент и=<р(х) сам является функцией от х, т.е. рассмотрим сложную функцию У ⁼/[ф(*)]- Если y=ftu) и и=ф(х) — дифференцируемые функции от своих аргументов, то производная сложной функции в соот­ветствии с теоремой, приведенной в §7.4, равна у' =f'{u)-u'.

Тогда дифференциал функции

dy=f(x) dx=f'(u)-u'dx=f(u) du,

ибо по формуле (9.2) u'dx=du. Итак,

(9.4)

dy=f'(u) du.

Последнее равенство означает, что формула дифференциата не изменяется, если вместо функции от независимой переменной х рассматривать функцию от зависимой переменной и. Это свойст­во дифференциала получило название инвариантности (т.е. неиз­менности) формы (или фдрмулы) дифференциала.

Однако в содержании формул (9.3) и (9.4) все же есть разли­чие: в формуле (9.3) дифференциал независимой переменной равен приращению этой переменной, т.е. ах=Ах, а в формуле (9.4) дифференциал функции du есть лишь линейная часть при­ращения этой функции Аи и только при малых Ах du» Аи.

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: