Основные теоремы дифференциального исчисления

Теорема Ферма. Если дифференцируемая на промежутке X функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке х₀ этого промежутка, то производная функции

в этой точке равна нулю, т.е. /' (х₀) = 0.

□ Пусть функция y-fix) дифференцируема на промежутке X и в точке д:₀ еХпринимает наименьшее значение (рис. 8.1).

Тогда Дх₀ +Дх;)^Д jc₀), если л:₀ +Ахе еХ и, следовательно, величина ^У⁼Л^хо⁺^^х)~Л^хо) ^ 0 при достаточ­но малых Ах независимо от знака Ах

Отсюда ^- > 0 при Дх>0 и ^- < 0
Дл: Ах

_ при Дх<0. Переходя к пределу при

Дх->0+ (справа) и при Дх-»0— (слева),

lim ■=- Лх->0- Дх

х получим lim —;

Дх->0+ Дх

Рис. 8.1

По условию функция у =Дх) диф­ференцируема в точке х₀, следовательно, ее предел при Дх->0 не

должен зависеть от способа стремления Дх->0 (справа или слева), т.е. lim — = lim —, откуда следует, что /' (хо) = 0.

Аналогично рассматривается случай, когда функция Дх) при­нимает в точке л;₀ наибольшее значение.И

на рис. 8.3 нарушено только одно условие: на рис. 8.3а — непре­рывность на отрезке [а, Ь], на рис. 8.36 — дифференцируемость на интервале (а, Ь), на рис. 8.3в — равенство значений Да)= Дй). В результате не существует такой точки % е (а,Ь), в которой

а)

Теорема Ролля является частным случаем теоремы Лагранжа. Теорема Лагранжа. Пусть функция у = Дх) удовлетворяет сле­дующим условиям: 1) непрерывна на отрезке [а, Ь]; 2) дифференцируема на интервале (а, Ь); Тогда внутри отрезка существует по крайней мере одна такая точка %е{а, Ь), в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке,

b-a □ Введем новую функцию g(x) следующим образом: .... f{b) - Да).. g(x)=fix)-1Л-1 — J-±-L (х-а). Ь-а Функция g(x) удовлетворяет условиям теоремы Ролля: она не­прерывна на отрезке [а, Ь], дифференцируема на интервале (я, Ь) и принимает на его концах равные значения:

Геометрический смысл теоремы Ферма очевиден: в точке наи­большего или наименьшего значения, достигаемого внутри проме­жутка X, касательная к графику функции параллельна оси абсцисс.

Теорема Ферма может быть использована для доказательства так называемых теорем о среднем, к рассмотрению которых мы переходим.

Теорема Ролля. Пусть функция у =/(*) удовлетворяет следую­щим условиям:

1) непрерывна на отрезке [а, Ь];

2) дифференцируема на интервале {а, Ь);

3) на концах отрезка принимает равные значения, т.е. j(a)=f(b).
Тогда внутри отрезка существует по крайней мере одна такая

точка £е(д, Ь), в которой производная функция равна нулю:

/'(§) = а

D На основании теоремы Вейерштрасса (см. § 6.7) функция,

непрерывная на отрезке, достигает на нем своего наибольшего М и наименьшего т значений. Если оба эти значения достигаются на концах отрезка, то по условию они равны (т.е. т=М), а это значит, что функция тождественно постоянна на отрезке [а, Ь]. Тогда производная равна нулю во всех точках этого отрезка. Если же хотя бы одно из этих значений — максимальное или мини­мальное — достигается внутри от­резка (т.е. т < М), то производная в соответствующей точке равна нулю

в силу теоремы Ферма.И

Отметим геометрический смысл теоремы Ролля (см.рис. 8.2): найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абс­цисс; в этой точке производная и будет равна нулю (заметим, что на рис. 8.2 таких точек две: ^ и £₂)• Если f(a)=j(b)=0, то теорему Ролля можно сформулировать так: между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной.

Следует отметить, что все условия теоремы Ролля существен­ны и при невыполнении хотя бы одного из них заключение тео­ремы может оказаться неверным. Так, для функций, приведенных

b - а Следовательно, существует точка

или

(а, Ь) такая, что g'(S) — 0

Ь-а

 

Заключение (8.1) теоремы Лагранжа может быть записано и в виде:

. (8.2)

Выясним механический и геометрический смысл теоремы Лагранжа.

Приращение fib)—fia) — это изменение функции на отрезке

№)-№

[а,

— средняя скорость изменения функции на

Ь-а

этом отрезке; значения же производной в точке — это "мгновенная" скорость изменения функции. Таким образом, теорема утверждает: существует хотя бы одна точка внутри от­резка такая, что скорость изменения функции в ней равна средней

У>	Л	В/
	Яа)Г!
	а 4	Ь х

скорости изменения функции на этом отрезке.

Геометрическая интерпретация теоремы Лагранжа приведена на рис. 8.4.

Рис.8.4

Если перемещать прямую АВ па­раллельно начальному положению, найдется хотя бы одна точка Е,е(а, Ь), в которой касательная к графику fix) и хорда АВ, проведенная через концы дуги АВ, параллельны (ибо в соответствии с (4.5) угловой коэф-

Ь-а

фициент секущей к_АВ =

а касательной — к = /'(!))•

Следствие. Если производная функции fix) равна нулю на некотором промежутке X, то функция тождественно постоянна, на этом промежутке.

□ Возьмем на рассматриваемом промежутке X отрезок [а, х]. Согласно теореме Лагранжа fix)—fia)=f'(E,)(x—a), где а<^<х. По условию/'(£)=0, следовательно, Дх)—Дд)=0, т.е. fix)=fia)=coiM.*

Правило Лопиталя

Теорема. Предел отношения двух бесконечно малых или беско­нечно больших функций равен пределу отношения их производных {конечному или бесконечному), если последний существует в указан­ном смысле.

Итак, если имеется неопределенность вида | — |или | — |, то

^ГТ- (8-3)

g(x)

П Рассмотрим доказательство теоремы для неопределенности

го"|

вида - прих->х₀.

Для простоты будем предполагать, что функции Дх) и g(x), a

также их производные непрерывны в точке х₀, причем lim f(x) =

х->х₀

)=0 и lim £(x) = £(x_o)=O.

В этом случае lim

^4 ^Ш ^1 ^ч •

g(x) x->x₀ g(x) - g(X₀)

Применяя теорему Лагранжа для функций fix) и g(x) на отрез­ке [х, х₀], получим

g(x) где х < %\ < xq, х < ^2 < ^хо •

При х-»х₀ в силу непрерывности производных f'(x) и g'(x) имеем /'(Si)->/'(х₀) и #'(12)-►£'(•*<))• Используя теорему о пределе частного двух функций, получаем равенство (8.3).и

Замечание. Обращаем внимание, что в правой части формулы (8.3) берется отношение производных, а не производная отношения.

[> Пример 8.1. Найти:

... х _..,. х*,,. log_ax а) шп —; б) lim —; в) lim °°.

Р е ш е н и е. а) Имеем неопределенность вида —. Приме-

L°°J няя правило Лопиталя, получим:

х'

lim— =

= lim-----

оо | *->«. (_е^ху

б) Имеем также неопределенность вида —. Применим пра-

[_ooj

вило Лопиталя [к]+1 раз, где [к] — целая часть числа t

 

loo] = - =hm

*->» ax ш2 д

Шп*1 = |-1=Ит

i^x In a I oo к{к-\). .\к-\к\)х

— 1X111

При каждом применении правила Лопиталя степень числите­ля будет уменьшаться на единицу и через [к]+1 раз станет отри­цательной, т.е. числитель обратится в бесконечно малую величи­ну (если к — не целое число; если к — целое, то в постоянную величину). Знаменатель же будет оставаться бесконечно большой

х^к

величиной. Таким образом, lim —т- =0.

*->■*> а

ч,. log0x Гоо] (log.x)',. в) шп Ьа, = — =hm v Ьа, ' = шп л;-»» х |_оо J х-^со (х)' х-+«

fcxK

——шп—_г=0> kina х-><*> х

()

х".. ах -------- = «, lim — = oo. logfl х *->» х

Правило Лопиталя дает возможность сравнения бесконечно больших величин: степенная функция х"~ бесконечно большая более высокого порядка, чем логарифмическая log_a x, а показа­тельная а^х — бесконечно большая более высокого порядка, чем

степенная х"; это означает, что lim [> Пример 8.2. Найти:

_е^х + _е^х _ 2
a) lim------- 5-----; б) lim x In x.

Р е ш е н и е. а)

<,*+<,-*_ 2 ГО].. (<?X+<T lim------- =----- = х = и111------------------- i О

2x

•2)'.. -^- = lim

Неопределенность вида I — I по-прежнему сохраняется. При-

меним правило Лопиталя еще раз:

О' „,

■=1.

,. е^х-е^х.. (е^х
lim —i---- = шп

2х х4Ь (2х)' х^Ь 2 б) Имеем неопределенность вида [Ооо]. Переписывая данное выражение в виде

lim (x In x) =[0-oo]= lim ——, получим неопределенность ви-

lim ^ = [-1= lim -^- = lim(-x)=0.^

x->0+ 1 [_ooj x->0+ 1 x->0

x "x²"

Правило Лопиталя является эффективным методом раскрытия неопределенностей. Однако применение его не всегда приводит к цели. О Пример 8.3. Найти:

_ч.. VxTT _сч,. x + sinx
a) lim ,; б) lim--- —.

_..•_ 2Vx + l _ „„ Vx-1 _

Р е ш е н и е. а) Если применить правило Лопиталя, то полу­чим

т.е. числитель и знаменатель просто меняются местами; неопре­деленность же сохраняется. Если применить правило Лопиталя вторично, то функция под знаком предела примет первоначаль­ный вид. Таким образом, применение этого правила в данном случае не позволяет раскрыть неопределенность. В то же время легко установить, что

lim

■= lim x-¥«> ijx — 1 x->°°

/x + 1

б) Если применить правило Лопиталя, т.е.

COSX

.. x + sinx Гоо] (x + sinx)'.. 1 +
шп----------- = — =шп^---------- ^-=шп —

COSX

x->ooX-SinX L°°J *-*°° \^х "■^{sm Х}У x-xol-

то можно сделать ошибочный вывод о том, что предел данной функции не существует, так как не существует lim cos x.

smx

x + sin x

= 1,

smx

1 На самом деле lim-------- = lim

I: x-»°o x - sin x

1-

 

да| — |. Применяя правило Лопиталя, получим

sinx

так как lim

X->°o X

=0 (см. пример 6.8в)>-

 

8.3. Возрастание и убывание функций

Напомним (см. § 5.3), что функция у = /(х) называется воз­растающей (убывающей) на промежутке X, если для любых Xj, х₂ еХ, х₂ > x_t верно неравенство /(х₂) >/(x_t) (f(x₂)</(х_х).

Теорема (достаточное условие возрастания функции). Если производная дифференцируемой функции положительна внутри некоторого промежутка X, то она возрастает на этом проме­жутке.

D Рассмотрим два значения XjH х₂ на данном промежутке X. Пусть х₂ > xj, x_t, х₂ е X. Докажем, что /(х₂) >/(x_t).

Для функции /(х) на отрезке [х_1;х₂] выполняются условия теоремы Лагранжа, поэтому

f(x₂)-fix_l)=f%)(x₂-x_l), (8.4)

где х_х <£< х₂, т.е. \ принадлежит промежутку, на котором произ­водная положительна, откуда следует, что f'(%)>0 и правая часть равенства (8.3) положительна. Отсюда Дх₂)—Дх,)>0 и Дх₂)>

>Л *,)•■•

Аналогично доказывается другая теорема.

Теорема (достаточное условие убывания функции). Если произ­водная дифференцируемой функции отрицательна внутри некото­рого промежутка X, то она убывает на этом промежутке.

Геометрическая интерпретация условия монотонности функ­ции приведена на рис. 8.5.

б)

а)

ж

Рис. 8.5 216

Если касательные к кривой в некотором промежутке направ­лены под острыми углами к оси абсцисс (рис.8.5а), то функция возрастает, если под тупыми (рис. 8.56), то убывает.

[> Пример 8.4. Найти интервалы монотонности функции у=

х

Решение. Имеем у' = 1.x—А. Очевидно у'>0 при х > 2 и у' <0 при х < 2, т.е. функция убывает на интервале (—<х>, 2) и воз­растает на интервале (2, оо), где х_о=2 — абсцисса вершины пара-

Заметим, что необходимое условие монотонности более слабое. Если функция возрастает (убывает) на некотором промежутке X, то можно лишь утверждать, что производная неотрицательна (неположительна) на этом промежутке: f'(x)>0 (/'(x)<0), хеХ, т.е. в отдельных точках производная монотонной функции может равняться нулю.

D Пример 8.5. Найти интервалы монотонности функции у = х^г.

Решение. Найдем производную у = Зх². Очевидно, что у' > >0 при х *■ 0. При х = 0 производная обращается в нуль..Функция же монотонно возрастает на всей числовой оси (см.рис.5.5).^

Экстремум функции

В определенном смысле материал этого параграфа наиболее ва­жен для решения задачи исследования функций и построения их графиков. Мы выделим наиболее важные, "узловые", точки функ­ции, нахождение которых во многом определяет структуру графика. Это точки экстремума — максимума и минимума функции.

Определение 1. Точка х₀ называется точкой максимума функ­ции f(x), если в некоторой окрестности точки х₀ выполняется нера­венство fix) <f(x₀) (см.рис. 8.6).

Определение 2. Точка х_{ называется точкой минимума функции fix), если в некоторой окрестности точки х₁ выполняется неравен­ство f(x) >f(x_x) (см.рис. 8.6).

Значения функции в точках х₀ и х₁ называются соответст­венно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции.

УН

Экстремум функции часто на­зывают локальным экстремумом, подчеркивая тот факт, что понятие экстремума связано лишь с доста­точно малой окрестностью точки х₀. Так что на одном промежутке

J

функция может иметь несколько экстремумов, причем может слу­читься, что минимум в одной точке больше максимума в дру-

8.6

Рис. 8.6

гой, например, на рис.

/mm (*2>>/max (*())• НаЛИЧИе МЭК-

симума (или минимума) в отдель­ной точке промежутка X вовсе не означает, что в этой точке функ­ция fix) принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (ми­нимум)).

Важность точек экстремума ил­люстрируется следующим приме­ром (см. рис. 8.7).

Рис. 8.7

Предположим, график функции У ⁼fi^x) имеет вид, изображенный на рисунке сплошной линией. Допустим, мы строим его по точ-

кам, и на рисунок нанесены точки 1, 3, 5, 7, 9. Тогда скорее всего мы получим кривую, изображенную пунктиром, которая совер­шенно не похожа на истинный график функции у =fix).

Если же на рисунок нанесены точки 2, 4, 6, 8, то качественная картина графика определена практически однозначно (по край­ней мере на промежутке, содержащем эти тёчки).

Необходимое условие экстремума. Если в точке х₀ дифферен­цируемая функция у =./(*) имеет экстремум, то в некоторой ок­рестности этой точки выполнены условия теоремы Ферма (см. § 8.1), и, следовательно, производная функции в этой точке рав­на нулю, т.е. /' (х_о)=0. Но функция может иметь экстремум и в

точках, в которых она не дифференцируема. Так, например, функция у=\ х | имеет экстремум (минимум) в точке х=0, но не дифференцируема в ней (см. пример 7.2 и рис.7.5). А функция

у=\х² также имеет в точке х=0 минимум (рис. 8.8), а производ-

ная ее в этой точке бесконечна: у' = —гт=, у' (0)=оо.

Рис.8.9

Рис. 8.8

Поэтому необходимое условие экстремума может быть сфор­мулировано следующим образом.

Для того, чтобы функция у =fix) имела экстремум в точке х₀,

необходимо, чтобы ее производная в этой точке равнялась нулю (f'(x₀) = 0) или не существовала.

Точки, в которых выполнено необходимое условие экстрему­ма, т.е. производная равна нулю или не существует, называются критическими (или стационарными). Обращаем внимание на то, что эти точки должны входить в область определения функции.

Таким образом, если в какой-либо точке имеется экстремум, то эта точка критическая. Очень важно, однако, заметить, что обратное утверждение неверно. Критическая точка вовсе не обя­зательно является точкой экстремума.

[>Пример 8.6. Найти критические точки функции и убедиться в наличии или отсутствии экстремума в этих точках:

а) у=х^г; б) у=х⁵ +1; в) у=Цх -1.

 

Р е ш е н и е. а) Производная у' = 2х. В точке х = О у' (0) = 0 и действительно в точке х = 0 функция у = х² имеет экстремум (см.рис. 5.6).

б) Функция у = х³ +1 возрастает на всей числовой оси по
свойству степенной функции. Производная у' = Зх² в точке х = 0
равна нулю, т.е. у' (0) = 0, но экстремума в точке х = 0 нет
(см.рис. 8.9).

в) Функция у=Ух - 1 также возрастает на всей числовой оси;

производная у' =

при х — 1 не существует, т.е. у' (1) =

= оо, но экстремума в этой точке нет (см.рис. 8.!()).►

 

У 1
	f
	a >	Co b.	X

Рис. 8.10 Рис. 8.11

Таким образом, для нахождения экстремумов функции требу­ется дополнительное исследование критических точек. Иными словами, требуется знать достаточное условие экстремума.

Первое достаточное условие экстремума. Теорема. Если при пе­реходе через точку х₀ производная дифференцируемой функции y=ftx) меняет свой знак с плюса на минус, то точка х₀ есть точка максимума функции у=Дх), а если с минуса на плюс, — то точка минимума.

□ Пусть производная меняет знак с плюса на минус, т.е. в не­котором интервале (а,х₀) производная положительна (f'(x)> >0), а в некотором интервале (х₀, Ь) — отрицательна (/' (х)<0). Тогда в соответствии с достаточным условием монотонности функция/(х) возрастает на интервале (а, х₀) и убывает на интер­вале (х₀, Ь), (см. рис. 8.11).

По определению возрастающей функции Д х₀) > Дх) при всех хе(а, х₀), а по определению убывающей функции Дх) < Дх₀) при всех хе(х₀, Ь), т.е. /(х₀) >/(х) при всех х е(а, Ь), следова­тельно, х₀ — точка максимума функции у =/(х).

Аналогично рассматривается случай, когда производная меня­ет знак с минуса на плюс.И

Отметим, что дифференцируемость функции в самой точке jc₀ не использовалась при доказательстве теоремы. На самом деле она и не требуется — достаточно, чтобы функция была непре­рывна в точке х₀.

L

О | х 0

а) б)

Рис. 8.12

Таким образом, достаточным условием существования экстре­мума функции у= f(x) в точке х₀ является изменение знака ее производной, т.е. углов наклона касательных к кривой.у=Дх): с острых на тупые (рис. 8.12а) при переходе через точку макси­мума или с тупых на острые (рис. 8.126) при переходе через точку минимума. Если изменения знака производной не происходит, то экстремума нет.

Схема исследования функции ^=Дх) на экстремум.

1°. Найти производную у '=/'(х).

2°. Найти критические точки функции, в которых производ­ная /'(х)=0 или не существует.

3°. Исследовать знак производной слева и справа от каждой
критической точки и сделать вывод о наличии экстремумов
функции. ¹

4°. Найти экстремумы (экстремальные значения) функции.

ОПример 8.7. Исследовать на экстремум функцию у =х(х— I)³.

 

х>0), следовательно, при х=

Решение. 1°. Производная функции у' = (х— I)³ +3х (х—

-I)² = (х-1)² (4х-1).

2°. Приравнивая производную к нулю, находим критические

точки функции x_l=—;x₂=l. (Точек, в которых производная не

существует, у данной функции нет — / '(х) определена на всей числовой оси).

3°. Нанесем критиче­ские точки на числовую прямую (рис. 8.13).

Для определения знака производной слева и

Рис. 8.13

справа от критической

точки л; = — выберем, на-4

пример, значения х — О и х = — и найдем / '(0) = —1 < 0 и /'(-)= - > 0; следовательно, /' (х) < 0 при всех х < -и /'(х)>0

на интервале (—; 1).

Аналогично устанавливаем, что/' (х)>0 и на интервале (1, ее).

Согласно достаточному условию х =---- точка минимума

4 данной функции. В точке х- 1 экстремума нет.

m i(i V 27

40. Находим _faia[-)=-[--l) =-—•►

Второе достаточное условие экстремума. Теорема. Если первая производная/' (х) дважды дифференцируемой функции равна нулю в некоторой точке х₀, а вторая производная в этой точке /" (х₀) положительна, то х₀ есть точка минимума функции /' (х); если /"(х₀) отрицательна, то х₀ — точка максимума.

□ Пусть /' (х₀)=0, а /" (х₀)>0. Это значит, что /" (х) = (f'(x))'> > 0 также и в некоторой окрестности точки х₀, т.е. /' (х) возрастает на некотором интервале (а, Ь), содержащем точку х₀.

Но /' (х_о)=О, следовательно, на интервале (а,х₀)/' (х) < 0, а на интервале (х₀, b) f (х) > 0, т.е. /' (х) при переходе через точ­ку х₀ меняет знак с минуса на плюс, т.е. х₀ — точка минимума.

Аналогично рассматривается случай/' (х_о)=О и/" (х_о)<О. ■ Схема исследования на экстремум функции у =/(х) с помо­щью второго достаточного условия в целом аналогична схеме, приведенной выше (совпадают полностью п.п. 1°, 2°, 4°). Отли­чие в п 3°, устанавливающем наличие экстремума: здесь необхо­димо найти вторую производную/" (х) и определить ее знак в каж­дой критической точке.

> Пример 8.8. Производитель реализует свою продукцию по це­не р за единицу, а издержки при этом задаются кубической зависи­мостью S(x)=ax+Xx³ (a<p, \>0). Найти оптимальный для производи­теля объем выпуска продукции и соответствующую ему прибыль.

Решение. Обозначим объем выпускаемой продукции х. Составим функцию прибыли С(х)=рх~(ах+Хх³), где рх — доход от реализуемой продукции.

1°. Находим С (х)=(р-а)-ЗХх².

2°. Находим критические точки: С (х)=(р-а)-ЗХх²=0, откуда
\р-а,_____________________________ \р-а

не рас-

(вторую критическую точку х₂ =

сматриваем по смыслу задачи).

3°. Находим С" (х)=—бАх и определяем знак второй производ-

ной при

= J - <0 (в данном случае С" (х)<0 при любом

прибыль С(х) максимальна.

4°. Находим максимум функции (т.е. максимальный размер прибыли)

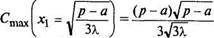
Второе достаточное условие экстремума утверждает, что если в критической точке х₀ /" (х_о)^О, то в этой точке имеется экс­тремум. Обратное утверждение, однако, неверно. Экстремум в критической точке может быть и при равенстве в ней нулю вто­рой производной.

 

т.е. прямая

f(x) x³ x²
k= lim = lim —=---:x= lim —=---- =1;

x" I i- f x,

/>= lim f/(x)-lxl = lim

■ - x = lim - ,. I =0.

4°. Поведение функции в бесконечности. Вычислим lim --

*-»+«= 1-х²

\ + х1

„2

=—1. В силу четности имеем также lim

 

Таким образом, наклонная асимптота графика функции имеет вид

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: