Возникновение предельных теорем теории вероятностей

На последующее развитие теории вероятностей огромное воздействие оказала идея, впервые высказанная и осуществленная Я. Бернулли рассматривать не только точные решения задач теории вероятностей, но и их асимптотические постановки при неограниченном увеличении некоторого параметра. В первую очередь следует указать на закон больших чисел в форме Я. Бернулли. Именно он послужил источником для различного рода уточнений как в 18-ом веке, так и в последующие столетия.

Я. Бернулли дал формулировку своей теоремы в отличном от принятого теперь виде, использовал для обозначения испытаний, при которых интересующее нас событие происходит, слова «плодовитый», «фертильный», а для противоположных исходов слово «стерильный».

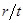«Пусть число фертильных случаев к числу стерильных случаев относится точно или приближенно как  или же это число относится к числу всех случаев как  или же как . Последнее отношение находится, следовательно, между  и . Нужно доказать, что можно произвести столь большое число опытов, что число появившихся фертильных наблюдений к числу всех опытов будет больше, чем , и меньше, чем 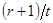». Ясно, что эта формулировка лишь словесно отличается от принятой теперь.

Книга «Искусство предложений» Я. Бернулли быта тщательно изучена его племянником Н. Бернулли. В его работе «О применении искусства предположений в вопросах прав», исходя из таблиц Граунта, он изучал вопрос о вероятности дожития до определенного возраста. На основании долголетних регистраций рождений он отметил тот факт, что мальчиков рождается больше, чем девочек. При этом отношение числа рождений мальчиков к числу рождений девочек оказывается, как он считал, равным 18:17.

Далее Н. Бернулли рассмотрел пример, когда имеется 14 000 рождений. Тогда, согласно формулам Н. Бернулли, имеет место равенство (  означает фактическое число рождений мальчиков)

Фактическое число рождений мальчиков зависит от случая. Приведенная формула позволяет вычислить вероятность того, что число рождений мальчиков будет заключено в указанных границах. Однако вычисления, которые при этом необходимо произвести, сложны.

В точности этот пример рассмотрен Лапласом в «Аналитической теории вероятностей». В качестве искомого значения вероятности неравенства 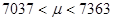  Лаплас указал величину 0.994303.

В двух последних изданиях книги Муавра «Доктрина шансов» был помещен перевод его статьи 1733 г. Согласно словам самого автора «Я помещаю здесь перевод моей работы, написанной 12 ноября 1733 года и сообщенной некоторым друзьям, но никогда не публиковавшейся». В кратком введении Муавр отметил, что для решения ряда задач теории вероятностей необходимо подсчитывать суммы членов биномиального распределения и что вычисления становятся громоздкими при больших значениях числа испытаний. В результате перед Муавром возник вопрос о разыскании асимптотической формулы. Эта задача была им благополучно решена. Основная трудность, которая при этом возникала, состояла в оценке факториала 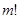 при больших значениях 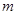. Муавр доказал, что , где , однако это его не удовлетворило и ему хотелось связать эту константу с ранее введенными в математику. Стирлинг показал, что . Известную формулу Стирлинга для приближенного вычисления факториала в случае больших чисел, таким образом, следовало бы назвать формулой Муавра. Использовав найденную им формулу «Стирлинга», Муавр первоначально выяснил, что в случае 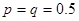 средний член бинома  асимптотически равен , а затем доказал локальную теорему, названную его именем. Далее Муавр получил локальную теорему для случая  фактически в принятом теперь виде.

Имея в руках локальную теорему, Муавр без затруднений сформулировал и интегральную, правда, только для симметричных границ.

Муавр отметил, что интегральную теорему можно использовать и для оценки неизвестной вероятности , т.е. для решения обратной задачи, задачи математической статистики.