Основы геодезических вычислений

Принципы вычислений. Вычисления — неотъемлемый элемент геодезических работ как во время измерений, так и в процессе об­работки их результатов. Способ и технические средства вычисле­ний зависят от сложности и объема работы. Для вычисления при­меняют счеты, логарифмические линейки, арифмометры, вычисли­тельные машины. В процессе работы используют справочные ма­териалы, таблицы, номограммы.

При вычислении соблюдают общие требования, что позволяет уменьшить вероятность ошибок и дает возможность получить ре­зультат наиболее простым путем. Прежде всего выбирают рацио-.нальную схему (алгоритм), обеспечивающую простоту, наглядность и однотипность вычислений, например результаты измерений и по­левых вычислений записывают в стандартных журналах, а после­дующих (камеральных) вычислений — в бланках или ведомостях. Все вычисления сопровождаются контролем —текущим и заклкь чительным. При текущем контроле проверяют правильность про­межуточных вычислений, при заключительном — окончательного •результата. Для этого либо вычисления выполняются параллельно и независимо друг от друга двумя работниками, либо результаты проверяют по контрольным формулам. Записи ведут четко и раз­борчиво: не допускается исправление неверно записанного или вы­численного числа по ранее написанному, ошибочное число зачер­кивают одной линией и над ним пишут правильное число.

В геодезических вычислениях приходится иметь дело преиму­щественно с приближенными числами. Для того чтобы добиться наибольшей степени приближения, соблюдают следующие правила.

В приближенном числе выделяют десятичные знаки, значащие цифры и верные цифры. Десятичными знаками считают все циф­ры, стоящие после запятой, значащими цифрами — все цифры чис­ла, кроме нулей, стоящих перед первой и после последней знача­щими цифрами (например, в числе 0,0107 четыре десятичных зна­ка и три значащих цифры). Верными называются цифры числа «заслуживающие доверия». Например, если при измерении линии с точностью до 1 м получается результат 285,41 м, верными будут цифры 285, последние две цифры неверные, «не заслуживающие доверия».

При вычислениях удерживают такое количество значащих цифр, десятичных знаков, знаков логарифма, которое обеспечива­ет нужную точность результатов и не загружает вычисления невер­ными или ненужными цифрами. В тех случаях, когда приближен­ное число содержит излишнее количество неверных значащих цифр, прибегают к округлению. Обычно руководствуются следующим пра­вилом: при выполнении приближенных вычислений число знача­щих цифр промежуточных результатов не должно превышать чис­ла верных цифр более чем на одну или две единицы. Окончатель­ный результат может содержать не более одной лишней значащей

цифры. Числа округляют по общим правилам: если следующая пос­ле оставляемой цифры меньше 5, ее и последующие цифры отбра­сывают, если больше 5 — к последней оставляемой цифре прибав­ляют единицу, например число я последовательно округляют так: 3,14159, 3,1416, 3,142, 3,14. Если в числе последняя цифра 5, то ее округляют до четной цифры, например 10,375 — до 10,38; 0,245 — до 0,24.

При выполнении арифметических действий с приближенными числами целесообразно руководствоваться следующими прави­лами: 1. При сложении или вычитании чисел с неодинаковым коли­чеством десятичных знаков оставляют столько десятичных знаков, сколько их имеет число с наименьшим количеством десятичных зна­ков, плюс один запасной знак. В сумме или разности оставляют

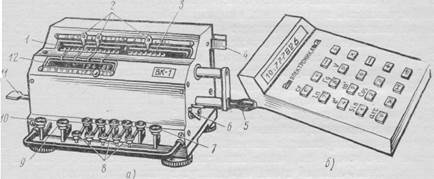
Рис. 32. Счетные машины:

а — клавишный арифмометр, б — микрокалькулятор «Электроника БЗ-37»; / — счетчик результатов, 2 —движки — запятые, 3 — счетчик оборотов, 4 — рычаг гашения счетчика оборотов, 5— рукоятка, 6 — рычаг гашения установки чисел, 7 — клавиша для отвода в крайнее левое положение набранного на клавиатуре числа, 8 — цифровые клавиши, 9, 10 — клавиши поразрядного передвижения установленного числа вправо и влево, // — рычаг гашения счетчика результатов, 12 — окно контроля установки чисел

такое количество десятичных знаков, какое имеет число с наимень­шим количеством знаков. 2. При умножении или делении чисел с неодинаковым количеством значащих цифр оставляют столько зна­чащих цифр, сколько их имеет число с наименьшим количеством зна­чащих цифр, плюс одна запасная цифра. В произведении или част­ном сохраняют столько значащих цифр, сколько их имеет число с наименьшим количеством значащих цифр. 3. При возведении чис­ла в степень в результате оставляют столько значащих цифр, сколь­ко их было в числе, возводимом в степень. 4. При извлечении кор­ня из числа в результате сохраняют столько значащих цифр, сколь­ко верных цифр имеет подкоренное число.

При вычислениях, связанных с умножением и делением чисел, возведением в степень и извлечением корня, применяют логариф­мический, нелогарифмический (натуральный) и бестабличный спо­собы, наиболее часто — нелогарифмический способ, основанный на применении вычислительных машин. Логарифмическим способом пользуются, когда вычислительных машин нет.

Счетные машины. Простейшая счетная машина — арифмо­метр— служит для выполнения арифметических действий, в ос­новном деления и умножения. Существует два вида арифмометров: рычажный и клавишный (рис. 32, а). Арифмометры обоих видов действуют по принципу механического набора участвующих в вы­числении цифр путем вращения рукоятки 5 соответствующее ко­личество раз.

Для инженерных расчетов применяют автоматические клавиш­ные электромеханические и электронные вычислительные машины. Наиболее совершенные — малогабаритные электронные вычислительные машины (микрокалькуляторы), на которых произ­водят от простых арифметических действий до сложных расчетов. Отличительная особенность этих машин — малые размеры и мас­са, удобство в работе — бесшумность и мгновенная скорость вычис­лений, т. е. быстродействие. Набор и все вычислительные команды производятся с помощью клавиш.

Микрокалькулятор «Электроника БЗ-23» выполняет четыре арифметических действия: сложение, вычитание, умножение и де­ление, «Электроника Б3-24г» имеет еще запоминающее устройство. Микрокалькуляторы «Электроника БЗ-18» и «Электроника БЗ-37» (рис. 32, б) выполняют четыре арифметических действия; вычисле­ние натуральных и десятичных логарифмов и антилогарифмов, три­гонометрических и обратных тригонометрических функций, извле­чение корня; возведение в степень, операции с постоянными числа­ми, с памятью. При вычислении тригонометрических функций ар­гумент может задаваться либо в градусной, либо в радианной мере.

Для сложных и больших по объему вычислений применяются малые и большие электронно-вычислительные машины (ЭВМ).

Первые ЭВМ появились в середине 40-х — начале 50-х годов. Это были ма­шины первого поколения, в которых в качестве основного физического элемента использовалась лампа, что обусловливало малую скорость вычислений, неболь­шую надежность, громоздкость машин. В середине 50-х годов появились ЭВМ второго поколения, в которых вакуумные лампы были заменены полупроводни­ковыми элементами. Эти машины и сейчас находятся в эксплуатации. Скорость их вычислений — 20—25 тыс. операций в секунду. Сейчас внедряются в произ­водство машины третьего поколения, в них использованы интегральные схемы, что позволило сократить размеры ЭВМ, увеличить объем памяти, повысить на­дежность. Разрабатываются миниатюрные и быстродействующие ЭВМ четвертого поколения и последующих

Вычисления с помощью ЭВМ выполняют по инструкции — про­грамме, содержащей сведения о последовательности действия при решении задачи. Процесс составления программы называется про­граммированием. Для многих часто встречающихся геодезических задач составлены стандартные программы их решения на ЭВМ.

Табличные и графические способы вычислений. Табличные способы вычислений основаны на использовании общих и специальных таблиц. Общими являются, например, таблицы лога­рифмов, квадратов чисел, специальными — таблицы, приращений координат, таблицы для разбивки круговых кривых.

По точности таблицы бывают двух видов: с одним и тем же

числом знаков после запятой или с одинаковым для всех значений аргументов числом значащих цифр. Последние таблицы точнее, по­этому их применяют для высокоточных вычислений. Прежде чем выбрать ту или иную таблицу, устанавливают, какое необходимое число знаков, чтобы обеспечить заданную точность вычислений. Например, при нахождении логарифмов натуральных чисел поль­зуются таблицами со столькими знаками, сколько верных • цифр в данном числе.

Графические способы вычислений основаны на применении номограмм. Номограмма представляет собой чертеж, являющийся изображением функциональной зависимости. По номо­грамме без вычислений определяют числовое значение одной пере­менной по числовым значениям других переменных, входящих в данную формулу.

Наиболее распространены номограммы из двойных шкал. При­мер такой шкалы — основная шкала логарифмической линейки, со­вмещенная со шкалой мантисс логарифмов.

Точность вычислений по номограммам зависит от их размера. Так, номограммы размером 20...40 см, построенные для геодези­ческих формул, позволяют получить 3...4 верных знака.

ГЛАВА VII