Общие сведения из теории погрешностей измерении

Погрешности и их виды. Измерения в геодезии рассматривают­ся с двух точек зрения: количественной, выражающей числовое зна­чение измеренной величины, и качественной, характеризующей ее точность.

Из практики известно, что даже при самой тщательной и акку­ратной работе многократные (повторные) измерения не дают оди­наковых результатов. Этот факт указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Отклонение результата измере­ния величины от ее истинного (точного) значения называется погрешностью измерения.

Величина погрешности характеризует точность измерений. Если обозначить истинное значение измеряемой величины X, а резуль­тат измерения /, то истинная погрешность измерения Д определится из выражения Д = /— X.

Любая погрешность результата измерения есть следствие дей­ствия многих факторов, каждый из которых порождает свою по­грешность. Погрешности, происходящие от отдельных факторов, называют элементарными. Погрешность результата измерения яв­ляется алгебраической суммой элементарных погрешностей.

Изучением основных свойств и закономерностей действия по­грешностей измерений, разработкой методов получения наиболее точного значения измеряемой величины и характеристик ее точно­сти занимается теория погрешностей измерений. Излагаемые в тео­рии погрешностей измерений методы решения задач позволяют

рассчитать необходимую точность предстоящих измерений и на основании этого расчета выбрать соответствующие приборы и тех­нологию измерений, а после производства измерений получить наи­лучшие их результаты и оценить их точность. Математической ос­новой теории погрешностей измерений являются теория вероятно­стей и математическая статистика.

Погрешности измерений разделяют по двум признакам: по ха­рактеру их действия и по источнику происхождения.

По характеру действия погрешности бывают: грубые, систематические и случайные.

Грубыми называются погрешности, превосходящие по абсолют­ной величине некоторый, установленный для данных условий изме­рений предел. Они происходят в большинстве случаев в результа­те промахов и просчетов исполнителя. Такие погрешности обнару­живаются повторными измерениями, а результаты, содержащие их, бракуются и заменяются новыми.

Систематическими погрешностями называются такие, которые по знаку или величине однообразно повторяются в многократных измерениях. Например, в длине линии из-за неточного знания дли­ны мерного прибора, из-за неточности уложения мерного прибора в створе этой линии и т. п. Влияние систематических погрешностей стремятся исключить из результатов измерений или ослабить тща­тельной проверкой измерительных приборов, применением соответ­ствующей методики измерений, а также введением поправок в ре­зультаты измерений.

Случайные погрешности — это погрешности, размер и влияние которых на каждый отдельный результат измерения остается не­известным. Величину и знак случайной погрешности заранее уста­новить нельзя. Однако теоретические исследования и многолетний опыт измерений показывают, что случайные погрешности подчине­ны определенным вероятностным закономерностям, изучение кото­рых дает возможность получить наиболее надежный результат и оценить его точность.

По источнику происхождения различают погрешно­сти приборов, внешние и личные.

Погрешности приборов обусловлены несовершенством измери­тельных приборов, например погрешность в угле, измеренном те­одолитом, ось вращения которого неточно приведена в вертикаль­ное положение.

Внешние погрешности происходят из-за влияния внешней ^сре­ды, в которой протекают измерения, например погрешность в от­счете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира сол­нечными лучами.

Личные погрешности — погрешности, связанные с особенностя­ми наблюдателя, например разные наблюдатели по-разному наво­дят зрительную трубу на визирную цель.

Так как грубые погрешности должны быть исключены из ре­зультатов измерений, а систематические исключены или ослаблены

до минимального допустимого предела, то проектирование изме­рений с необходимой точностью, оценку результатов выполненных измерений производят, основываясь на свойствах случайных по­грешностей.

Свойства случайных погрешностей. Случайные погрешности ха­рактеризуются следующими свойствами.

1.При определенных условиях измерений случайные погрешно­
сти по абсолютной величине не могут превышать известного пре­
дела, называемого предельной погрешностью. Это свойство позво­
ляет обнаруживать и исключать из результатов измерений грубые
погрешности.

2. Положительные и отрицательные случайные погрешности
примерно одинаково часто встречаются в ряду измерений. Это
свойство помогает выявлению систематических погрешностей.

3. Чем больше абсолютная величина погрешности, тем реже она
встречается в ряду измерений.

4. Среднее арифметическое из случайных погрешностей измере­
ний одной и той же величины, выполненных при одинаковых усло­
виях, стремится к нулю при неограниченном возрастании числа из­
мерений. Это свойство, называемое свойством компенсации, мож­
но математически записать так, Нт[Л]/«=0, где [] — знак суммы,

П^- оо

т. е. [А]=Д₁+Д₂+Л₃+ — +А_П, «— число измерений.

Последнее свойство случайных погрешностей позволяет уста­новить принцип получения из ряда измерений одной и той же вели­чины результата, наиболее близко подходящего к ее истинному значению, т. е. наиболее точного. Таким результатом является среднее арифметическое (арифметическая середина) из п измерен­ных значений данной величины. При бесконечно большом числе измерений п Г\т[1\/п=Х.

При бесконечном числе измерений арифметическая середина х=[1]/п содержит остаточную случайную погрешность, однако от точного значения X измеряемой величины она отличается меньше, чем любой результат / непосредственного измерения. Это позволя­ет при любом числе измерений, если п>1, принимать арифметиче­скую середину за окончательное значение измеренной величины. Точность окончательного результата тем выше, чем больше п.

Средняя квадратическая, предельная и относительная погреш­ности. Для правильного использования результатов измерений не­обходимо знать, с какой точностью, т. е. с какой степенью близо­сти к истинному значению измеряемой величины, они получены. Характеристикой точности отдельного измерения в теории погреш­ностей служит предложенная Гауссом средняя квадратиче­ская погрешность т, вычисляемая по формуле

где п — число измерений данной величины.

Эта формула применима для случаев, когда известно истинное значение измеряемой величины. Такие случаи в практике встре­чаются редко. В то же время из измерений можно получить ре-

 

до минимального допустимого предела, то проектирование изме­рений с необходимой точностью, оценку результатов выполненных измерений производят, основываясь на свойствах случайных по­грешностей.

Свойства случайных погрешностей. Случайные погрешности ха­рактеризуются следующими свойствами.

1.При определенных условиях измерений случайные погрешно­
сти по абсолютной величине не могут превышать известного пре­
дела, называемого предельной погрешностью. Это свойство позво­
ляет обнаруживать и исключать из результатов измерений грубые
погрешности.

2. Положительные и отрицательные случайные погрешности
примерно одинаково часто встречаются в ряду измерений. Это
свойство помогает выявлению систематических погрешностей.

3. Чем больше абсолютная величина погрешности, тем реже она
встречается в ряду измерений.

4. Среднее арифметическое из случайных погрешностей измере­
ний одной и той же величины, выполненных при одинаковых усло­
виях, стремится к нулю при неограниченном возрастании числа из­
мерений. Это свойство, называемое свойством компенсации, мож­
но математически записать так, Нт[ ]/n=0, где [ ] — знак суммы,

т. е. [ ]=Д₁+Л₂+Лз +... + Лп, п — число измерений.

Последнее свойство случайных погрешностей позволяет уста­новить принцип получения из ряда измерений одной и той же вели­чины результата, наиболее близко подходящего к ее истинному значению, т. е. наиболее точного. Таким результатом является среднее арифметическое (арифметическая середина) из п измерен­ных значений данной величины. При бесконечно большом числе измерений п Ит[1\/п=Х.

При бесконечном числе измерений арифметическая середина х=[1]/п содержит остаточную случайную погрешность, однако от точного значения X измеряемой величины она отличается меньше, чем любой результат / непосредственного измерения. Это позволя­ет при любом числе измерений, если «>1, принимать арифметиче­скую середину за окончательное значение измеренной величины. Точность окончательного результата тем выше, чем больше п.

Средняя квадратическая, предельная и относительная погреш­ности. Для правильного использования результатов измерений не­обходимо знать, с какой точностью, т. е. с какой степенью близо­сти к истинному значению измеряемой величины, они получены. Характеристикой точности отдельного измерения в теории погреш­ностей служит предложенная Гауссом средняя квадратиче­ская погрешность т, вычисляемая по формуле

где, п- —-число измерений данной величины.

Эта формула применима для случаев, когда известно истинное значение измеряемой величины. Такие случаи в практике встре­чаются редко. В то же время из измерений можно получить ре-

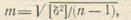
зультат, наиболее близкий к истинному значению, — арифметиче­скую середину. Для этого случая средняя квадратическая погреш­ность одного измерения подсчитывается по формуле Бесселя:

где б — отклонения отдельных значений измеренной величины от арифметической середины, называемые вероятнейшими по­грешностями, причем [6]=0.

Точность арифметической средины, естественно, будет выше точности отдельного измерения. Ее средняя квадратическая по­грешность М определяется по формуле

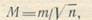
где т — средняя квадратическая погрешность одного измерения, вычисляемая по формуле (5) или (.6).

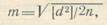
а среднего результата из двух измерений — по формуле

Часто в практике для контроля и повышения точности опреде­ляемую величину измеряют дважды — в прямом и обратном на­правлениях, например длину линий, превышения между точками. Из двух полученных значений за окончательное принимается сред­нее из них. В этом случае средняя квадратическая погрешность одного измерения подсчитывается по формуле

где а — разности двукратно измеренных величин; п — число раз­ностей (двойных измерений).

В соответствии с первым свойством случайных погрешностей для абсолютной величины случайной погрешности при данных условиях измерений существует допустимый предел, называемый предельной погрешностью. В строительных нормах пре­дельная погрешность называется допускаемым отклоне­нием.

Теорией погрешностей измерений доказывается, что абсолютное большинство случайных погрешностей (68,3%) данного ряда изме­рений находится в интервале от 0 до ±т, в интервал от 0 до ±2т попадает 95,4, а от 0 до ±3/п —99,7% погрешностей. Таким обра­зом, из 100 погрешностей данного ряда измерений лишь пять мо­гут оказаться больше или равны 2т, а из 1000 погрешностей толь­ко три будут больше или равны Зт. На основании этого в качест­ве предельной погрешности А_пред для данного, ряда измерений при­нимается утроенная средняя квадратическая погрешность, т. е. А_Пред=Зт. На практике во многих работах для повышения требо­ваний к точности измерений принимают А_Пред=2т. Погрешности измерений, величины которых превосходят А_Пред, считают грубыми.

Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по вели-

чине относительной погрешности. Относительной погреш­ностью называется отношение абсолютной погрешности к зна­чению самой измеренной величины. Относительная погрешность выражается в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая по­грешность измерения линии длиной / = 110 м при т^=2 см равна т.1/1= 1/5500, а относительная предельная погрешность при А_Пред= = 3т Д_пред//=1/1800.

Оценка точности результатов измерений. Точность результатов многократных измерений одной и той же величины оценивают в та­кой последовательности. 1. Находят вероятнейшее (наиболее точ­ное для данных условий) значение измеренной величины по форму­ле арифметической середины х=[[\[п. 2. Вычисляют отклонения $1 = 11—х каждого значения измеренной величины 1\, 1%,..., 1_п от значения арифметической середины. Контроль вычислений: [б]=0. 3. По формуле Бесселя (6) вычисляют среднюю квадратическую погрешность одного измерения. 4. По формуле (7) вычисляют сред­нюю квадратическую погрешность арифметической середины. 5. Если измеряется линейная величина, то подсчитывают относи­тельную среднюю квадратическую погрешность каждого измерения и арифметической середины. 6. При необходимости подсчитывают предельную погрешность одного измерения, которая может слу­жить допустимым значением погрешностей аналогичных измере­ний.

Пример 1. Длина линии местности измерена шесть раз. Требуется опреде­лить вероятнейшее значение длины линии и оценить точность выполненных из­мерений. Результаты измерений и вычислений записывают по форме, приведенной в табл. 1.

Таблица 1

 

М п/п	/, м	В, см	8», см"	Вычисления
	121,75	—1	I	т = УТ1 см/(6— 1) =
2 3	121,81 121,77	+5 + 1	25 I	= 4,0 см; М = 4,0 см/Т^6~=
	121,70	—6		= 1,6 см; т{/1= 1/3000
5 6	121,73 121 79	-3 +3	9 9	М/1= 1/7600 Дпред= 12 см
Среднее 121,76	-Г

Оценку точности по разностям двойных измерений производят в такой по­следовательности. 1. Вычисляют среднее значение из двойных измерений. 2. Вы­числяют разности Л двойных измерений. 3. По формуле (8) вычисляют среднюю квадратическую погрешность одного измерения. 4. По формуле (9) вычисляют среднюю квадратическую погрешность среднего результата из двух измерений.

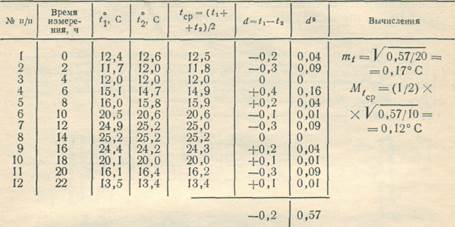
Пример 2. На метеостанции температура воздуха измерялась в разное время суток двумя одинаковыми термометрами.

Требуется определить среднюю квадратическую погрешность измерения тем­пературы воздуха одним термометром и среднего значения из одновременных

 

измерений двумя термометрами. Значения измеренных температур воздуха и оценку точности измерений записывают по форме, приведенной в табл. 2.

Таблица 2

ГЛАВА VIII

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: