 |
Масштабы изображения на плоскости
|
|
|
|
Масштаб — это отношение длины з линии на чертеже, плане, карте к длине 5 горизонтального приложения, соответствующей линии в натуре, т. е.з: 5. Масштаб обозначается либо дробью (числовой), либо в виде графических изображений.
Числовой масштаб представляет собой правильную дробь, у которой числитель равен 1:5/5=1/(5/5) = 1/М. Знаменатель М показывает, во сколько раз^ уменьшены линии местности при изображении их на плане. Например, для масштаба 1: 100 единице длины на плане соответствует 100 таких же единиц на местности, или 1 см.на плане— 100 см (1,0 м) на местности. Чем больше знаменатель числового масштаба, тем больше степень уменьшения, т. е. тем мельче масштаб. Из двух числовых масштабов более крупный тот, у которого знаменатель меньше.
Используя значение 1/М числового масштаба и зная длину 5 приложения линии на местности, можно по формуле
S=S/М
определить величину отрезка на плане или по формуле

определить величину линии на местности, зная длину 5 этого отрезка на плане.
Пример 1. Длина отрезка s=142 м. Найти величину изображения этого отрезка на плане масштаба 1: 2000.
По формуле (1) получим:
s=142 м/2000 = 0,071 м = 7,1 см.
Пример 2. На плане масштаба 1: 500 величина отрезка между двумя точками s = 14 6 см. Определить длину s этой линии на местности. По формуле (2) находим s = 14,6 см X 500=7300 см = 73 м.
|
При решении задач по карте или плану пользоваться числовым масштабом трудоемко, так как приходится производить арифметические вычисления. В этом случае строят графические масштабы — линейный и поперечный.
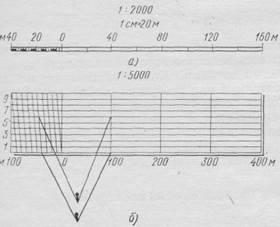
| Рис. 8. Графические масштабы: а — линейный, б — поперечный |
Линейный масштаб (рис. 8, а) представляет собой шкалу с делениями, соответствующими данному числовому масштабу. Для построения линейного масштаба на прямой линии откладывают несколько раз расстояние, называемое основанием масштаба. Длину основания принимают от 1 до 2,5 см. Первое основание делят на десять равных частей и на правом конце его пишут нуль, а на левом — то число метров или
|
|
|
километров, которому на местности соответствует в данном масштабе основание. Вправо от нуля над каждым делением надписывают значения соответствующих расстояний на местности (на рис. 8 изображен линейный масштаб для числового масштаба 1: 2000).
Поперечный масштаб применяют для измерений и построений повышенной точности. Обычно поперечный масштаб гравируют на металлических пластинах, линейках или на транспортирах. Для заданного числового масштаба он может быть построен на чертеже. Поперечный масштаб (рис. 8, б) строят следующим образом. На прямой линии, как и при построении линейного масштаба, откладывают несколько раз основание масштаба и первый отрезок делят на десять частей. Деления надписывают так же, как и при построении линейного масштаба. Из каждой точки подписанного деления восставляют перпендикуляры, на которых откладывают десять отрезков, равных десятой доле основания. Через точки, по-
лученные на перпендикулярах, проводят прямые линии, параллельные основанию. Верхнюю линию над первым основанием делят также на десять равных частей. Полученные точки верхних и нижних делений на первом отрезке соединяют, как показано на рисунке. Полученные линии называются трансверсалями. Расстояния между смежными трансверсалями составляют десятую долю основания, а между нулевой вертикальной линией и смежной с ней трансвер-салью — от одной сотой до десятой его доли.
Поперечный масштаб с основанием 2 см, изображенный на рис. 8, б, имеет подписи, соответствующие числовому масштабу 1: 5000. Основание масштаба соответствует 100 м на местности, десятая его часть—10 м, сотая—1 м. Если, например, в этом масштабе надо на плане отложить длину, равную на местности 146 м, правую ножку циркуля-измерителя совмещают с точкой 100 м справа от нуля, а левую — с точкой 40 м слева от нуля. Затем измеритель поднимают на шесть делений вверх и раздвигают до точки, соответствующей 146 м.
|
|
|
Применение любого масштаба, даже поперечного, не может обеспечить точности выше определенного предела, зависящего от свойств человеческого глаза. Невооруженным глазом с расстояния нормального зрения (25 см) можно оценить на плане размер, не превосходящий 0,1 мм (детали объектов местности меньше 0,1 мм изобразить на плане нельзя). Точность масштаба характеризуется горизонтальным расстоянием на местности, соответствующим на плане 0,1 мм. Например, для планов, вычерченных в масштабе 1:500, 1:1000, 1:2000 точность масштаба соответственно равна 0,05, 0,1, 0,2 м.
Точностью масштаба определяется степень обобщения (генерализации) подробностей, которые могут быть изображены на плане (карте) того или иного масштаба.
Для того чтобы акцентировать внимание на каких-то элементах чертежа, карты, плана, эти элементы изображают внемасштабно, т. е. с другой степенью уменьшения или увеличения. Увеличенными в произвольном масштабе изображают на схематических планах городов исторические, культурные памятники, театры, вокзалы (рис. 9), на мелкомасштабных картах кружки городов, толщины рек, на чертежах — условные обозначения, стыковые швы, маркировку изделия. По такому внемасштабному изображению нельзя производить никаких измерений. Разномасштабно, т. е. в определенном масштабе, но отличном от масштаба данного чертежа, показывают узлы, детали на строительных и машиностроительных чертежах; при изображении плана дороги, проходящей по однообразной местности, выделяют в крупном масштабе только места пересечения дорогой рек, населенных пунктов, дорог иного назначения и т. п. Таким образом, на одном и том же плане, чертеже, на одной карте изображения могут быть даны в разных масштабах, а в некоторых случаях и в натуральную величину.

Рис. 9. Пример внемасштабного изображения — план города
ГЛАВА II
|
|
|


