 |
Компоновка узла сопряжения пролётных и концевых балок и
|
|
|
|
Механизма движения крана
Перед тем как начать компоновку узла сопряжения балок, необходимо выбрать двигатель и редуктор механизма передвижения крана по таблице 7.1 [3, с.161].
Окончательно выбираем двигатель типа МТВ-112-6,
редуктор типа Ц2-300,
тормоз типа ТТ-160.
(Основные размеры и параметры выбранных механизмов берём из приложений [1, с.290]).
Компоновка узла сопряжения балок показана на рис. 2.6.
Проверочный расчёт и уточнённая конструктивная проработка
Проверочный расчёт выполняем одновременно с конструктивной проработкой балки моста.
Назначение расчётных комбинаций нагрузок для проверки
Прочности металлоконструкции
Прочность балки при её общем изгибе в двух плоскостях проверяем на действие нагрузок комбинации I.1.Б. [1, с.116].
Определение величины вертикальных нагрузок
Для определения расчётных вертикальных нагрузок необходимо найти коэффициент толчков. Для этого находим.
Вес пролётной части моста:
, (3.1)
где 
- распределённая нагрузка, 
;
- пролёт моста, 
,
.
Приведённая масса моста и тележки:
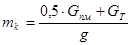, (3.2)
где 
- вес тележки;
- ускорение свободного падения,
.
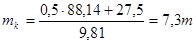Фактический коэффициент жёсткости моста:
, (3.3)
.
Парциальная частота собственных поперечных колебаний моста
, (3.4).
.
Определяем коэффициент толчков по выражению:
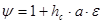, (3.5.)
где 
- высота ступеньки стыка рельсов;
- коэффициент, зависимости от скорости движения крана и параллельной частоты
колебаний;
- коэффициент, зависящий от схемы крана и вида нагрузки.
по графику рис.6.3. [1, с.118],
, для путей в эксплуатации [1, с.118],
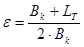, (3.6)
где 
- база крана;
|
|
|
- колея тележки,
.
.
Коэффициент толчков для веса тележки;
.
Коэффициент толчков для веса груза;
.
Тогда вертикальные нагрузки будут равны;
Весовая постоянная распределённая нагрузка:
, (3.7).
Сосредоточенные нагрузки:
, (3.8).
Сосредоточенные нагрузки:
, (3.9).
Определим расчётное давление колеса тележки:
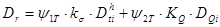, (3.10),
.
Находим равнодействующую воздействия тележки на мост:
.
Определим расстояние, показанное на рис.2.1.
.
Определим суммарный изгибающий момент по формуле 2.8, соответствуя компоновке рис.2.6.
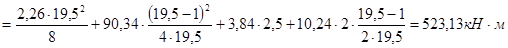
Определение величины горизонтальных нагрузок
При 
, т.е. при 
горизонтальные инерционные нагрузки равны:
;
;
.
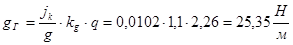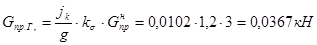Горизонтальная нагрузка на одно колесо:
, (3.10),
.
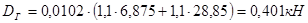Равнодействующая воздействия тележки на мост:
.
Суммарный горизонтальный изгибающий момент:
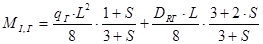, (3.11).
Момент в узле соединения пролётной и концевой балок со стороны колеса:
, (3.12)
где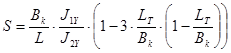 
, (3.13);
;
;
.
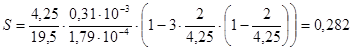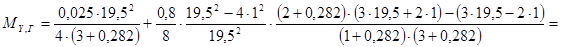
Проверка прочности балки
Коэффициент неполноты расчёта принимаем по формуле (2.9) 
.
Расчётная зависимость:
, (3.14)
где 
- изгибающий момент в вертикальной и горизонтальной плоскостях;
- момент сопротивления балки при изгибе в вертикальной и горизонтальной плоскостях;
- расчётное сопротивление материала.
.
;
.
Таким образом, прочность средней части балки при общем изгибе в двух плоскостях обеспечена.
Расчёт шага диафрагм из условия прочности рельса
Ребра жёсткости
Фактическая гибкость стенки пролётной балки в её средней части:
.
При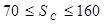 
для малоуглеродистых сталей достаточно устанавливать только основные поперечные рёбра жёсткости [1, с.126].
Диафрагмы будем выполнять из листового проката.
Ширину выступающей части ребра определим по условию [1, с.128]:
|
|
|
, (3.15).
.
Толщина ребра из условия обеспечения его устойчивости [1, с.128].
, (3.16).
.
(принимаем 
).
Момент инерции ребра относительно плоскости стенки в соответствии с формулой [1, с.128].
, (3.17)
.
Окончательно принимаем: 
; .
Тогда момент инерции относительно плоскости стенки:
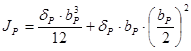, (3.18).
.
Проверку прочности поперечного ребра по условиям работы его верхней кромки на сжатие по формулам [1, с.129].
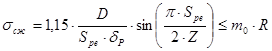, (3.129)
где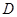 
- давление колеса тележки;
- длина линии контакта рельса и пояса под ребром;
- расчётное сопротивление материала при работе на сжатие;
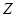- расчётная зона распределения давления колеса по ребру для сварки балок [1, с.129].
, (3.20)
где 
- момент инерции пояса и рельса относительно собственных нейтральных осей;
;
(принимаем для кранового рельса КР80 по табл. [1, с.310].
.
Для кранового рельса:
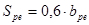, (3.21)
где 
- ширина подошвы рельса;
[1, с.310].
.
;
при 
; 
;
;
,
следовательно прочность верхней кромки диафрагмы обеспечена.
Шаг рёбер
Шаг основных поперечных рёбер жёсткости, являющихся опорами для рельса, определяют из условия прочности последнего.
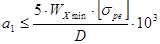, (3.22)
где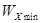 
- наименьший момент сопротивления рельса;
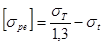, (3.23)
где 
- предел текучести материала,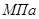 
;
- напряжения в рельсе от действия продольных сил, при отсутствии гарантийного прижатия рельса к поясу 
пренебрегаем.
[5, с.326].
.
, [5, с326].
.
Учитывая, что пояс балки достаточно тонкий для обеспечения его прочности при действии местных напряжений от давления колёс тележки, принимаем конструктивно шаг диафрагм 
.
Для отсеков примыкающих к опорам, шаг основных поперечных рёбер 
, в последующих отсеках их шаг может увеличиться до 
, т.е.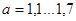 
.
Прочность верхнего пояса
При контакте подошвы рельса с поясом балки пояс находится в плоском напряжённом состоянии и его прочность нужно проверять по условию [1, с.129].
, (3.24)
где 
, 
- напряжение в балке от её общего изгиба в продольном направлении.
- местные, нормальные напряжения в поясе, соответственно вдоль и поперёк продольной оси балки.
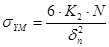, (3.25);
, (3.26)
где 
- сила, передающаяся на поясной лист через рельс от давления ходового колеса;
|
|
|
- толщина пояса.
При 
,
, (3.27)
где 
- расстояние между стенками балки в свету;
- расстояние между диафрагмами;
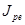- момент инерции рельса в вертикальной плоскости;
- коэффициенты, принимаемые по таблице. 6.17…6.19 [1, с.129].
При 
;
;
;
;
;
.
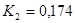
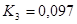
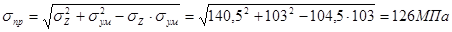При 
;
.
Þ прочность верхнего пояса обеспечена.
|
|
|
