 |
QUEUE OCH ; включение в очередь
|
|
|
|
QUEUE OCH ; включение в очередь
………
DEPART OCH ; выход из очереди Текст программы после редактирования приводится ниже:; GPSSW File PRODOVEC. GPS
********************************
*Моделирование работы магазина*
********************************
; Имитация прихода покупателей GENERATE 7, 5 ; приход покупателей ADVANCE 5, 3 ; знакомство с товаром; Имитация работы магазина QUEUE OCH ; включение в очередь SEIZE PROD ; обращение к продавцу DEPART OCH ; выход из очереди ADVANCE 3, 2 ; покупка товаров RELEASE PROD ; освобождение продавца TERMINATE ; уход покупателей; Задание времени моделирования GENERATE 240 ; время работы модели TERMINATE 1 ; уменьшение общего времени моделирования на 1 мин START 1 ; система пропускает по одному покупателю В этой модели момент включения каждого транзакта в очередь OCH совпадает с моментом его обращения к оператору SEIZE, т. к. оператор QUEUE выполняется в модельном времени мгновенно. Каждый транзакт находится в очереди до тех пор, пока не займет устройство PROD. Момент занятия устройства совпадает с моментом выхода транзакта из очереди. В данный момент очередь OCH имеет естественную интерпретацию как очередь посетителей к продавцу, а длина очереди интерпретируется как число посетителей в очереди. Дополнительные статистические данные для данного примера содержат следующую информацию:
QUEUE MAX CONT. ENTRY ENTRY(0) AVE. CONT. AVE. TIME AVE. (-0) RETRY
OCH 1 0 31 27 0. 032 0. 248 1. 924 0
Расшифровка полученной информации: QUEUE (Очередь)– номер или имя очереди – PROD; MAX (Максимальное содержание) – максимальная длина очереди в течение периода моделирования - 1; CONT. (Текущее содержание) – текущее содержимое очереди в конце процесса моделирования - 0; ENTRY (Число входов) – общее количество входов транзактов в очередь в течение времени моделирования - 31; ENTRY(0) (Число нулевых входов) – общее количество входов транзактов в очередь с нулевым временем ожидания - 27; AVE. CONT. (Среднее содержимое) – среднее значение содержимого очереди в течение времени моделирования – 0, 032; AVE. TIME (Среднее время) – среднее время пребывания одного транзакта в очереди с учетом всех входов в очередь – 0, 248; AVE. (-0) (Среднее время без нулевых входов) – среднее время пребывания одного транзакта в очереди без учета «нулевых» входов в очередь – 1, 924; RETRY (Повторные входы) – количество транзактов, ожидающих выполнения специального условия, зависящего от состояния очереди - 0.По приведенной статистической информации можно сделать следующие выводы:
|
|
|
1) максимальная длина очереди в течении 4 часов работы магазина – 1 покупатель;
2) среднее время пребывания покупателя в очереди – 0, 248 мин.
Для того чтобы сформировать таблицу с информацией о посещении покупателями данного магазина, воспользуемся оператором TABLE (Таблица). Оператор табулирования TABULATE (Табулировать), выполняющий сбор данных по времени и числу обслуживания в системе, записывается стем же именем таблицы, которое было определено в операторе TABLE. Для данного примера можно записать: MAG TABLE M1, 2, 2, 5 ; формирование таблицы………TABULATE MAG ; табулировать магазин Текст программы после соответствующего редактирования приводится ниже:; GPSSW File PRODOVEC. GPS
********************************
*Моделирование работы магазина*
********************************
; Имитация прихода покупателейMAG TABLE M1, 2, 2, 5 ; формирование таблицы GENERATE 7, 5 ; приход покупателей ADVANCE 5, 3 ; знакомство с товаром; Имитация работы магазина QUEUE OCH ; включение в очередь SEIZE PROD ; обращение к продавцу DEPART OCH ; выход из очереди ADVANCE 3, 2 ; покупка товаров RELEASE PROD ; освобождение продавца TABULATE MAG; табулировать магазин TERMINATE ; уход покупателей; Задание времени моделирования GENERATE 240 ; время работы модели TERMINATE 1 ; уменьшение общего времени моделирования на 1 мин START 1 ; система пропускает по одному покупателю Дополнительные выходные статистические данные для данного примера содержат следующую информацию:
|
|
|
TABLE MEAN STD. DEV. RANGE RETRY FREQUENCY CUM. %
MAG 8. 181 2. 687 0
2. 000 - 4. 000 2 6. 45
4. 000 - 6. 000 7 29. 03
6. 000 - 8. 000 4 41. 94
8. 000 - _ 18 100. 00
Информация о таблицах: TABLE (Таблица) – имя или номер таблицы или Q – таблицы – MAG; MEAN (Средняя) – среднее значение табулируемого аргумента – 8, 181; STD. DEV. (Среднеквадратическое отклонение) – оценка среднеквадратического отклонения – 2, 687; RANGE (Область) – нижний и верхний пределы частотного класса – 2-4; RETRY (Повторные входы) – количество транзактов, ожидающих выполнения специального условия, зависящего от состояния данной таблицы - 0; FREQUENCY (Частота) – суммарная величина, которая формируется при попадании табулируемого аргумента в указанные границы - 2; CUM % (Суммарный процент) – величина частоты в процентах к общему количеству значений табулируемого аргумента – 6, 45. Для большей наглядности выведем график того, как меняется длина очереди к продавцу за весь период моделирования. Для данного примера он будет выглядеть как на рис. 1. 2.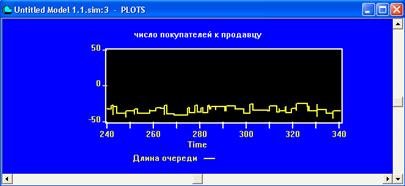
Рис. 1. 2. Помимо данных, представляемых в отчете в виде таблицы, при наличии оператора TABLE, можно вывести информацию в виде гистограммы, иллюстрирующей распределение времени обслуживания транзакта. Для данного примера она будет выглядеть как показано на рис. 1. 3. 
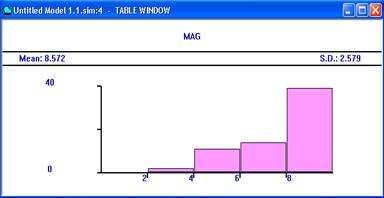Рис. 1. 3. Расчет характеристик системы по ее аналитической модели Функционирование СМО можно представить как последовательную смену ее возможных состояний, каждое из которых характеризуется количеством заявок (покупателей, рабочих, машин, неполадок) в системе. Поскольку эта величина имеет случайный характер, наличие n заявок задается вероятностью - Pn. Вероятность Po характеризует состояние, когда в системе нет заявок и канал обслуживания простаивает.
|
|
|
Важными параметрами функционирования СМО являются среднее число заявок, находящихся в системе – Nс. и средняя длина очереди - No. Исходными параметрами, характеризующими СМО, являются:
число каналов обслуживания (касс, компьютеров, ремонтных бригад) - M;
интенсивность поступления заявок на обслуживание, т. е. среднее число входящих заявок в единицу времени - λ ;
интенсивность обслуживания заявок каналом – μ .
Интенсивность поступления заявок на обслуживание определяется как величина, обратная среднему времени между поступлениями двух смежных заявок (tP): λ =1/tP, для данного примера λ =1/7=0, 143 мин-1.
Интенсивность обслуживания заявок определяется как величина, обратная среднему времени обслуживания одной заявки (tо): μ =1/tо, для данного примера μ =1/3=0, 333 мин-1.
Вероятность простоя канала определяется как Po=1-ρ , где ρ – коэффициент загрузки системы ρ =λ /μ , для данного примера ρ =0, 143/0, 333=0, 429 мин-1. Тогда Po=1-0, 429=0, 571. Загрузка, меньшая 1, говорит о том, что очередь к каналу не будет бесконечно большой.
Среднее число заявок Nс, находящихся в системе определяется из формулы
Nс=ρ /(1-ρ )=0, 429/(1-0, 429)=0, 751.
Среднее число заявок, находящихся в очереди No, будет вычислено так:
No=ρ Nс=0, 429·0, 751=0, 322.
Среднее время ожидания обслуживания определяется
tож=Nc/μ =3·0, 751=2, 253 мин-1.
Среднее время пребывания заявки в системе вычисляется
tc=1/μ (1-ρ )=3/0, 571=5, 253 мин-1.
Отчет по лабораторной работе
В отчете по лабораторной работе необходимо привести:
· формулировку цели работы;
· постановку задачи в соответствии с вариантом задания;
· аналитический расчет заданных характеристик;
· листинг программы на языке GPSS;
· результаты моделирования в виде отчетов,
· результаты моделирования в виде графика и гистограммы;
· выводы по работе.
Варианты индивидуальных заданий
|
|
|
