 |
14) Оценка точности функции измеренных величин.
|
|
|
|
14) Оценка точности функции измеренных величин.
1 – математическая обработка результатов геодезических измерений
2 – средние арифметическое результатов геодезических измерений
3 – среднее весовое значение результатов геодезических измерений
4 – уравнительные вычисления
5 – уравнивание геодезических измерений
15) Принцип измерения горизонтального и вертикального углов на местности.
Горизонтальный угол – это двугранный угол между отвесными плоскостями, проходящими через его стороны.
Для измерения горизонтального угла над его вершиной на отвесной линии помещают центр градуированного круга – лимба, - установленного горизонтально. Тогда угол между направлениями на местности будет равен разности отсчетов между сечениями лимба (a и b) вертикальными плоскостями, проходящими через линии OA' и OB' на местности. Если круг оцифрован по часовой стрелке, то β = b – a.
Измерение вертикальных углов (углов наклона) производится при помощи вертикального круга теодолита. Для удобства измерений вертикальных углов необходимо, чтобы при горизонтальном положении визирной оси (и нахождении в нуль-пункте пузырька цилиндрического уровня при алидаде) отсчёт по вертикальному кругу был нулевым. Однако это условие далеко не всегда выполняется. Отсчёт по вертикальному кругу, когда визирная ось горизонтальна, а пузырёк уровня при алидаде находится в нуль-пункте, называется местом нуля. Для измерения угла наклона зрительную трубу при положении КЛ наводят на некоторую точку A и, приведя пузырек в нуль-пункт, берут отсчёт Л. Аналогично берут отсчёт П. Тогда угол наклона (для теодолитов со шкалами вертикального круга с двойной оцифровкой, например, 4Т30) может быть найден как ν = Л – МО = МО – П, где место нуля МО = (Л+П)/2. Правильность измерения вертикальных углов контролируется постоянством МО. Точность измерения вертикальных углов зависит в первую очередь от погрешности отсчёта. Из других причин следует упомянуть вертикальную рефракцию (которую при длине менее 300 м можно не учитывать).
|
|
|
16) Решение прямой геодезической задачи
Прямой геодезической задачей - называют вычисление геодезических координат - широты и долготы некоторой точки, лежащей на поверхности земли, по координатам другой точки и по известным длине и дирекционному углу данного направления, соединяющей эти точки.
Для определения координат точки в прямой геодезической задаче обычно применяют формулы:
1) нахождения приращений:

2) нахождения координат:
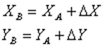
17) Решение обратной геодезической задачи
В обратной геодезической задаче находят дирекционный угол и расстояние:
1. вычисляют румб по формуле:
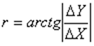
2. находят дирекционный угол в зависимости от четверти угла:
| четверти: | Первая четверть | Вторая четверть | Третья четверть | Четвертая четверть |
| знак приращения | +X, +Y | -X, +Y | -X, -Y | +X, -Y |
| диреционный угол | a = r | a = 180 - r | a = 180 + r | a = 360 - r |
3. определяют расстояние между точками:

18) Основные части теодолита. Оси теодолита и их взаимное расположение.
Основными частями теодолита являются горизонтальный и вертикальный круги, зрительная труба, цилиндрический уровень, подъёмные винты, винты закрепительные (алидад вертикального и горизонтального кругов и лимба горизонтального круга) и наводящие (алидад вертикального и горизонтального кругов и лимба горизонтального круга).
В принципиальной схеме теодолита выделяют четыре основных оси:
1. ОО1 - ось вращения прибора (вертикальная ось теодолита),
2. UU1 - ось цилиндрического уровня (касательная к внутренней поверхности ампулы в нуль-пункте),
|
|
|
3. WW1 – визирная ось зрительной трубы (прямая, соединяющая оптический центр объектива и крест сетки нитей),
4. VV1 - ось вращения зрительной трубы.
|
|
|


