 |
Краткий теоретический материал к задаче 3
|
|
|
|
Образец решения задач и их оформления
Краткий теоретический материал к задаче 1
СКАЛЯРНОЕ ПОЛЕ В ПРОСТРАНСТВЕ
Пусть  – произвольная область пространства. Будем говорить, что в области
– произвольная область пространства. Будем говорить, что в области  задано скалярное поле, если в этой области задана скалярная функция
задано скалярное поле, если в этой области задана скалярная функция  ,
,  .
.
Функция  , определяющая скалярное поле, называется функцией поля в пространстве.
, определяющая скалярное поле, называется функцией поля в пространстве.
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Пусть 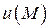 – заданное скалярное поле в области
– заданное скалярное поле в области  ,
, 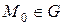 – заданная точка, а
– заданная точка, а
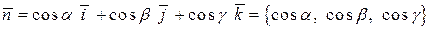
– заданный единичный вектор.
Производная скалярного поля 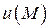 в точке
в точке 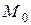 по направлению единичного вектора
по направлению единичного вектора 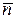 , обозначаемая
, обозначаемая  , вычисляется по формуле
, вычисляется по формуле
(1) 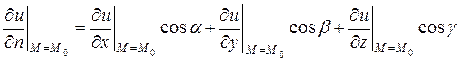 .
.
Пусть 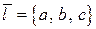 – произвольный ненулевой вектор. Если
– произвольный ненулевой вектор. Если 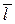 не является единичным вектором, то для вычисления производной скалярного поля
не является единичным вектором, то для вычисления производной скалярного поля 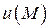 в точке
в точке  по направлению вектора
по направлению вектора 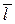 , необходимо найти единичный вектор
, необходимо найти единичный вектор 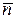 , сонаправленный с вектором
, сонаправленный с вектором 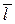 :
:
 ,
,
а затем, полагая,
 ,
,
используют формулу (1).
ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
Пусть 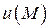 – заданное скалярное поле в области
– заданное скалярное поле в области  . Градиентом скалярного поля
. Градиентом скалярного поля 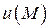 , обозначаемым символом
, обозначаемым символом  , называется вектор, проекциями которого являются частные производные функции
, называется вектор, проекциями которого являются частные производные функции 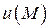 по соответствующим переменным:
по соответствующим переменным:
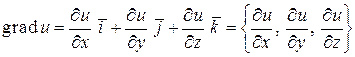 ,
,
Градиент скалярного поля 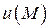 в точке
в точке 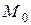 вычисляется по формуле
вычисляется по формуле
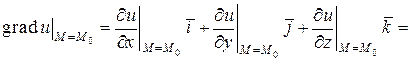
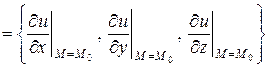 .
.
Задача 1
Даны скалярное поле 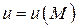 и точки
и точки  и
и  . Вычислить:
. Вычислить:
1) производную функции 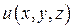 в точке
в точке 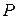 по направлению вектора
по направлению вектора 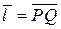 ;
;
2) градиент функции 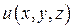 в точке
в точке 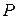 .
.
| Задача 1 Образец |
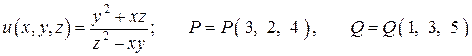 . .
|
Решение
1) Производная от функции 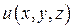 в точке
в точке 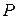 по направлению вектора
по направлению вектора  находится по формуле
находится по формуле
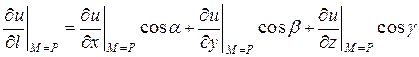 ,
,
где  ,
, 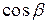 ,
, 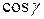 – направляющие косинусы вектора
– направляющие косинусы вектора 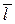 , то есть проекции единичного вектора
, то есть проекции единичного вектора 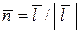 на координатные оси. Имеем
на координатные оси. Имеем
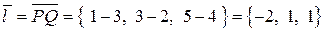 ,
,
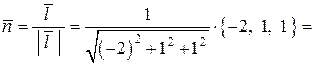
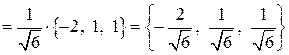 ,
,
 ,
, 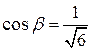 ,
, 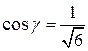 .
.
Найдем частные производные функции 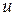 :
:
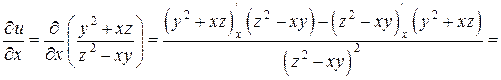
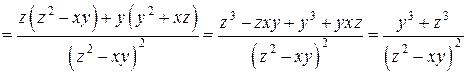 ,
,
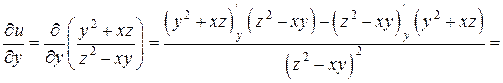
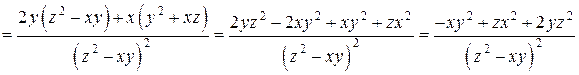 ,
,
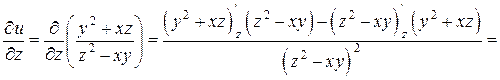
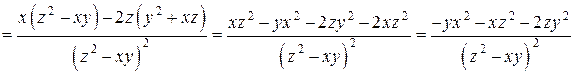
и вычислим их значения в точке 
|
|
|
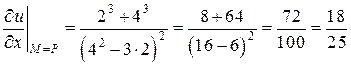 ,
,
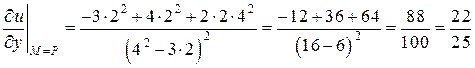 ,
,
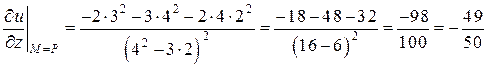 .
.
Таким образом,
 .
.
2) Градиент функции  в точке
в точке  вычисляется по формуле
вычисляется по формуле
 .
.
Используя вычисленные ранее значения частных производных, имеем
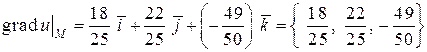 .
.
Ответ: 1)  ,
,
2) 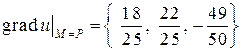 .
.
Краткий теоретический материал к задаче 2
ВЕКТОРНОЕ ПОЛЕ В ПРОСТРАНСТВЕ
Пусть  – произвольная область пространства. Будем говорить, что в области
– произвольная область пространства. Будем говорить, что в области  задано векторное поле, если в этой области задана векторная функция
задано векторное поле, если в этой области задана векторная функция
(1) 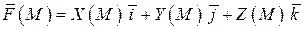 ,
,
где
(2) 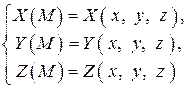
– заданные функции.
Векторная функция 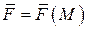 , определяющая векторное поле, называется функцией поля в пространстве.
, определяющая векторное поле, называется функцией поля в пространстве.
ПОТОК ВЕКТОРНОГО ПОЛЯ
Потоком векторного поля  через поверхность
через поверхность  в направлении единичного нормального вектора
в направлении единичного нормального вектора 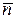 называется поверхностный интеграл
называется поверхностный интеграл
(3)  ,
,
где 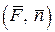 – скалярное произведение векторов
– скалярное произведение векторов  и
и 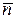 , а
, а 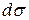 – дифференциал площади поверхности
– дифференциал площади поверхности  .
.
ВЫЧИСЛЕНИЕ ПОТОКА ЧЕРЕЗ ЧАСТИ ПОВЕРХНОСТИ
Рассмотрим задачу вычисления потока 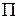 векторного поля
векторного поля  через заданную поверхность
через заданную поверхность  в направлении единичного нормального вектора
в направлении единичного нормального вектора 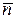 .
.
Если поверхность  в пространстве задана уравнением
в пространстве задана уравнением
(4) 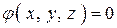 ,
,
то единичный нормальный вектор 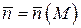 в точке
в точке 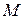 определяется равенством
определяется равенством
(5) 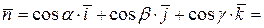
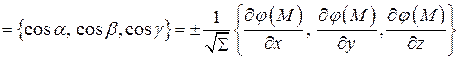 .
.
Знак  или
или 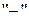 берется в зависимости от выбранной стороны двусторонней поверхности
берется в зависимости от выбранной стороны двусторонней поверхности  .
.
Если поверхность  является плоскостью, заданной уравнением
является плоскостью, заданной уравнением
(6) 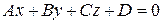 ,
,
то единичный нормальный вектор 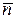 во всех точках
во всех точках 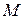 имеет одно и то же значение, и равное
имеет одно и то же значение, и равное
(7) 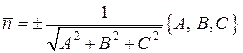 .
.
Рассмотрим задачу вычисления потока  векторного поля
векторного поля  через заданную поверхность
через заданную поверхность  в направлении единичного нормального вектора
в направлении единичного нормального вектора  .
.
Если поверхность  однозначно проектируется на плоскость
однозначно проектируется на плоскость  в область
в область 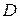 , то дифференциал площади поверхности равен
, то дифференциал площади поверхности равен
(9) 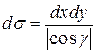
и вычисление потока сводится к вычислению двойного интеграла по области 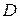 :
:
(10)  ,
,
где 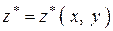 получается из уравнения поверхности (4).
получается из уравнения поверхности (4).
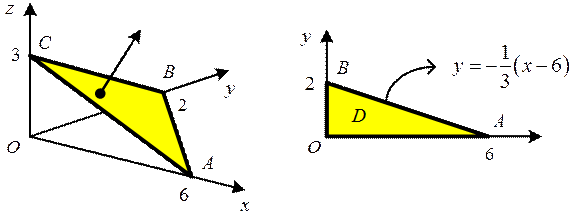
Задача 2
Даны векторное поле 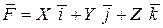 и плоскость
и плоскость 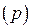 , которая совместно с координатными плоскостями образует пирамиду
, которая совместно с координатными плоскостями образует пирамиду 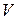 с вершиной в начале координат. Пусть
с вершиной в начале координат. Пусть  – основание пирамиды. Вычислить поток векторного поля
– основание пирамиды. Вычислить поток векторного поля  через поверхность
через поверхность  в направлении внешней нормали
в направлении внешней нормали 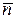 .
.
|
|
|
| Задача 2 Образец |
|
Решение
Рассматриваемая пирамида  и ее проекция
и ее проекция  на плоскость
на плоскость  изображены на рисунке.
изображены на рисунке.
Поток векторного поля  через поверхность
через поверхность  в направлении внешней нормали
в направлении внешней нормали 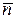 найдем с помощью поверхностного интеграла
найдем с помощью поверхностного интеграла
 .
.
Нормальным вектором плоскости 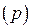 является вектор
является вектор  . Так как единичный нормальный вектор поверхности
. Так как единичный нормальный вектор поверхности  образует с осью
образует с осью 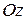 острый угол, то
острый угол, то 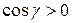 . Поэтому, направляющими косинусами нормального вектора являются
. Поэтому, направляющими косинусами нормального вектора являются
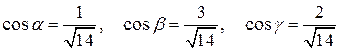 .
.
Отсюда
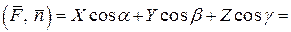
 ,
,
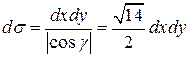 .
.
Из уравнения плоскости 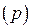 и области
и области 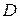 находим:
находим:
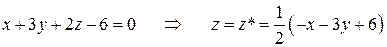 ,
,
 .
.
Далее, имеем,
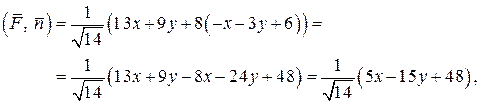
и, следовательно,
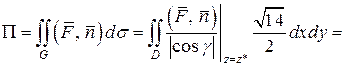
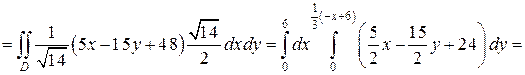
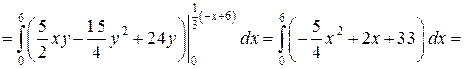
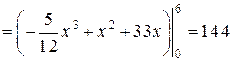 .
.
Ответ: 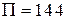
Краткий теоретический материал к задаче 3
|
|
|


