 |
Дивергенция векторного поля
|
|
|
|
Пусть в области  задано векторное поле
задано векторное поле
(1) 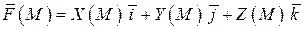 ,
,
где
(2) 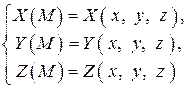
– заданные непрерывные функции.
Дивергенцией векторного поля  называется скалярная функция
называется скалярная функция
(3)  .
.
ФОРМУЛА ГАУССА–ОСТРОГРАДСКОГО
Пусть 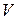 – пространственное тело,
– пространственное тело,  – поверхность, ограничивающая область
– поверхность, ограничивающая область 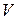 , а
, а 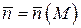 – внешний единичный нормальный вектор к поверхности
– внешний единичный нормальный вектор к поверхности  в точке
в точке 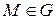 .
.
Если функции  ,
, 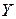 ,
, 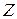 непрерывны в области
непрерывны в области 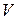 и частные производные
и частные производные 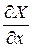 ,
, 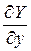 ,
,  – суть непрерывные функции в этой области, то поток векторного поля
– суть непрерывные функции в этой области, то поток векторного поля  через замкнутую поверхность
через замкнутую поверхность  в направлении внешней нормали, равен тройному интегралу от дивергенции
в направлении внешней нормали, равен тройному интегралу от дивергенции 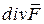 по области
по области 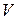 :
:
(4) 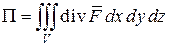 .
.
Эта формула называется формулой Гаусса – Остроградского.
Задача 3
Вычислить поток векторного поля  через всю поверхность тела
через всю поверхность тела 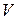 в направлении внешней нормали.
в направлении внешней нормали.
| Задача 3 Образец |
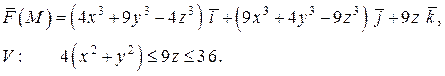
|
Решение
Поток векторного поля  через всю поверхность тела
через всю поверхность тела 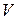 в направлении внешней нормали, вычислим по формуле Гаусса-Остроградского
в направлении внешней нормали, вычислим по формуле Гаусса-Остроградского
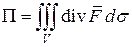 ,
,
где 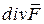 – дивергенция векторного поля,
– дивергенция векторного поля, 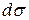 – элемент объема.
– элемент объема.
Дивергенция 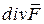 данного векторного поля
данного векторного поля  вычисляется по формуле
вычисляется по формуле
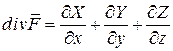 .
.
По условию задачи
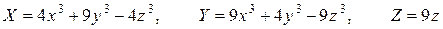 .
.
Поэтому,
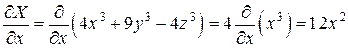 ,
,
 ,
,
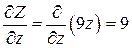 ,
,
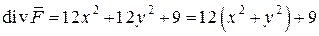 .
.
Таким образом,
 .
.
Для вычисления тройного интеграла перейдем к цилиндрическим координатам:
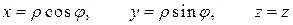 .
.
Данное тело  и его проекцию
и его проекцию 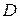 на плоскость
на плоскость 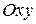 изобразим на рисунке.
изобразим на рисунке.
Найдем границы изменения переменных интегрирования и подынтегральные данные в новых переменных:
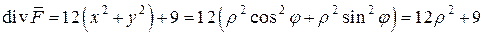 ,
,
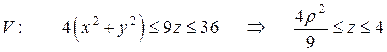 ,
,
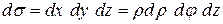 ,
,
 ,
,
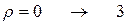 ,
,
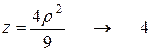 .
.
Произведем вычисления:
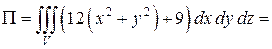
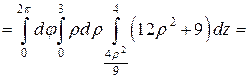
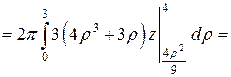
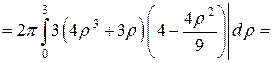
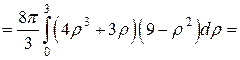
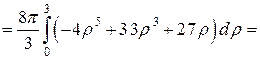
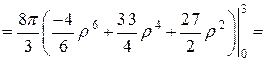
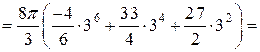
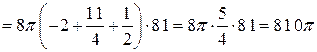 .
.
Ответ: 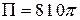
Краткий теоретический материал к задаче 4
ЦИРКУЛЯЦИЯ ВЕКТОРНОГО ПОЛЯ
Пусть в области  задано векторное поле
задано векторное поле
(1) 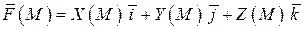 ,
,
где
(2) 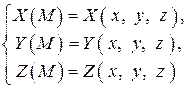
– заданные непрерывные функции.
Пусть также задана гладкая кривая  , на которой выбрано положительное направление (положительная ориентация). Через
, на которой выбрано положительное направление (положительная ориентация). Через 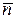 обозначим единичный вектор, касательный к кривой
обозначим единичный вектор, касательный к кривой  , направление которого совпадает с направлением кривой
, направление которого совпадает с направлением кривой  .
.
|
|
|
Линейным интегралом от векторного поля  вдоль ориентированной кривой
вдоль ориентированной кривой  называется криволинейный интеграл первого рода от скалярного произведения
называется криволинейный интеграл первого рода от скалярного произведения 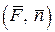 :
:
(3)  ,
,
где 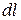 – дифференциал длины дуги
– дифференциал длины дуги 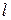 кривой
кривой  .
.
Если  – радиус-вектор произвольной точки
– радиус-вектор произвольной точки 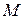 кривой
кривой  , то справедливо равенство
, то справедливо равенство
(4) 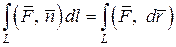 .
.
Линейный интеграл можно записать с помощью криволинейного интеграла второго рода:
(5) 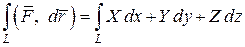 .
.
Если  является силовым полем, то линейный интеграл определяет величину работы этого поля вдоль линии
является силовым полем, то линейный интеграл определяет величину работы этого поля вдоль линии  .
.
Если  является замкнутой кривой (замкнутым контуром), то линейный интеграл называется циркуляцией
является замкнутой кривой (замкнутым контуром), то линейный интеграл называется циркуляцией  векторного поля
векторного поля  по замкнутому контуру
по замкнутому контуру  :
:
 .
.
РОТОР ВЕКТОРНОГО ПОЛЯ
Ротором ( или вихрем) векторного поля  называется векторная функция определяемая равенством
называется векторная функция определяемая равенством
(6) 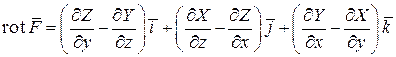 .
.
Ротор векторного поля можно также вычислить как определитель третьего порядка
(7) 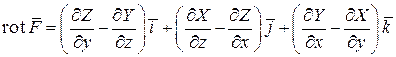 .
.
ФОРМУЛА СТОКСА
Пусть координаты векторного поля  – функции
– функции  ,
, 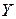 ,
, 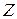 непрерывные и имеют непрерывные частные производные. Тогда циркуляция векторного поля
непрерывные и имеют непрерывные частные производные. Тогда циркуляция векторного поля  по замкнутому контуру
по замкнутому контуру  равна потоку ротора этого вектора через любую поверхность
равна потоку ротора этого вектора через любую поверхность  , натянутую на контур
, натянутую на контур  :
:
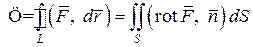 ,
,
где направление единичного нормального вектора 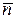 согласовано с ориентацией контура
согласовано с ориентацией контура  , то есть из конца нормали обход контура в выбранном направлении был виден против хода часовой стрелки.
, то есть из конца нормали обход контура в выбранном направлении был виден против хода часовой стрелки.
Эта формула называется формулой Стокса.
Задача 4
При помощи теоремы Стокса найти циркуляцию векторного поля 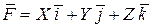 по замкнутому контуру, образованного пересечением плоскости
по замкнутому контуру, образованного пересечением плоскости 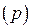 с координатными плоскостями в положительном направлении оси
с координатными плоскостями в положительном направлении оси 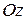 :
:
| Задача 3 Образец |
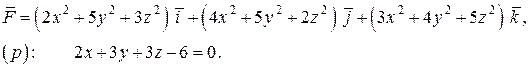
|
Решение
Для составления чертежа запишем уравнение плоскости 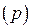 в «отрезках»:
в «отрезках»:
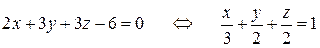 .
.
Найдем точки пересечения этой плоскости с координатными осями:
|
|
|
 ;
;
Замкнутым контуром  является замкнутая ломанная
является замкнутая ломанная 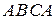 треугольника
треугольника 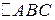 . Из таблицы 3 определим, что этот треугольник принадлежит
. Из таблицы 3 определим, что этот треугольник принадлежит 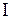 октанту.
октанту.
Проекцию треугольника 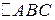 на плоскость
на плоскость 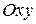 обозначим через
обозначим через  .
.
Составим чертеж.
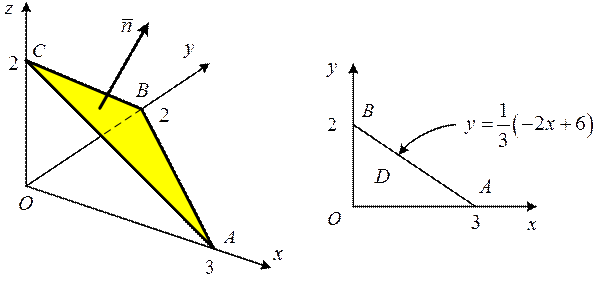
Запись в условие задачи: «в положительном направлении оси  » означает, что если смотреть из конца оси
» означает, что если смотреть из конца оси  на обход контура
на обход контура  , то его направление будет противоположно ходу часовой стрелки. Таким же свойством должен обладать единичный нормальный вектор плоскости
, то его направление будет противоположно ходу часовой стрелки. Таким же свойством должен обладать единичный нормальный вектор плоскости 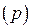 . Из двух нормальных векторов плоскости
. Из двух нормальных векторов плоскости
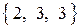 и
и  ,
,
только первый обладает этим свойством. Соответствующим единичным нормальным вектором является вектор
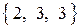 ,
,
составляющий острый угол с положительным направлением оси 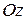 .
.
Ротор векторного поля вычисляется по формуле:
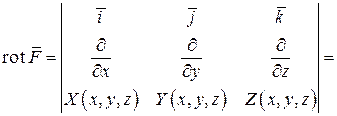
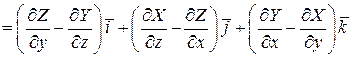 .
.
По условию задачи
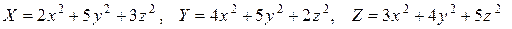 .
.
Найдем частные производные:
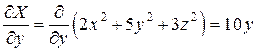 ,
,
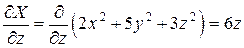 ,
,
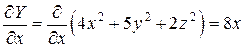 ,
,
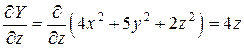 ,
,
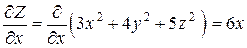 ,
,
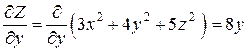 .
.
Вычислим ротор:
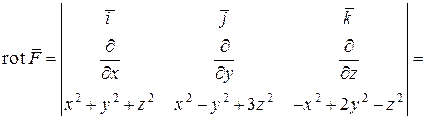
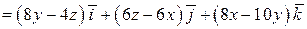 .
.
Циркуляцию  векторного поля
векторного поля  по замкнутому контуру
по замкнутому контуру  можно вычислить по формуле Стокса
можно вычислить по формуле Стокса
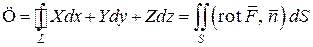 ,
,
где 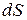 – элемент площади поверхности
– элемент площади поверхности  , то есть треугольника
, то есть треугольника 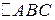 с замкнутым контуром
с замкнутым контуром  .
.
Так как
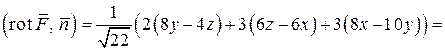
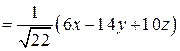 ,
,
 ,
,
 ,
,
то подставляя из уравнения плоскости 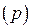 значения
значения  :
:
 ,
,
получим
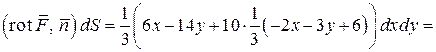
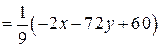 .
.
Найдем искомую циркуляцию:
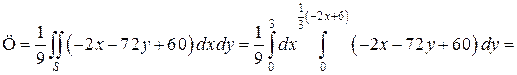
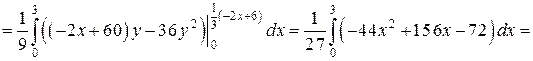
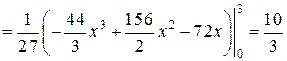 .
.
Ответ: 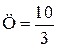
|
|
|


