 |
Краткий теоретический материал к задачам 5 – 7
|
|
|
|
ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ
КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Основные понятия, связанные с функцией комплексной переменной, вводятся так же, как и в вещественном случае.
Пусть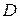 
и 
– два множества комплексных чисел. Если каждому комплексному числу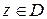 
ставится в соответствие комплексное число 
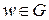, то говорят, что на множестве 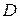задана функция комплексной переменной (ФКП), принимающая значения в множестве :
.
Если записать числа 
и 
в алгебраической форме
,
то действительная часть 
и мнимая часть 
ФКП являются функциями вещественных переменных 
и 
:
.
ПРЕДЕЛ ФКП
Комплексное число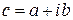 
называется пределом ФКП в точке 
, если существуют пределы вещественной части 
и мнимой части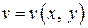 
ФКП 
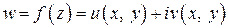в точке 
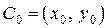и имеют место равенства
.
НЕПРЕРЫВНОСТЬ ФКП
ФКП называется непрерывной в точке , если вещественные функции и ,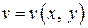 
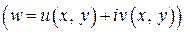являются непрерывными в точке .
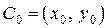Функция, непрерывная в каждой точке области 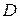, называется непрерывной в области точке .
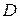ПРОИЗВОДНАЯ ФКП
Производной ФКП в точке называется величина
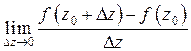
и обозначается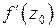 
:
.
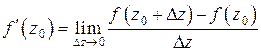Запись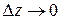 
означает стремление 
к нулю по любой кривой, по любому направлению.
Функция, имеющая производную в точке 
, называется дифференцируемой в точке . Функция, дифференцируемая в каждой точке области, называется дифференцируемой в области.
Непрерывность функции в точке является необходимым условием дифференцируемости функции в этой точке, то есть если функция дифференцируема в точке, то она непрерывна в этой точке.
УСЛОВИЯ КОШИ-РИМАНА
Если ФКП 
дифференцируема в точке 
, то в точке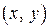 
существуют частные производные ее действительной части 
и мнимой части 
у имеют место равенства
(1) 
Равенства (1) называются условиями Коши-Римана.
|
|
|
Если данные функции и дифференцируемы в точке 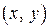и в этой точке выполняются условия Коши-Римана (1), то функция дифференцируема в точке .
Для производной функция справедливо любое из следующих представлений:
, 
,
, 
.
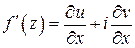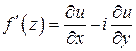ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФКП
Пусть дана вещественная функция 
. Требуется определить ФКП 
таким образом, чтобы при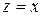 
ее свойства совпадали с известными свойствами функции . Для решения поставленной задачи используется ряд Тейлора функции :
.
Подставляя в ряд Тейлора вместо вещественной переменной комплексную переменную , получим степенной ряд, которого и примем в качестве функции :
.
Используя вышеприведенный способ определения ФКП, введем простейшие элементарные функции (многочлен степени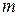 
, показательную функцию 
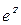, тригонометрические функции 
и 
, гиперболические функции 
и 
, логарифмическую функция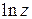 
).
1) Многочлен степени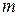
определяется естественным образом, как сумма различных степеней .
2) Для показательной функции 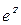получим представление
(2) 
.
Отсюда, в частности, получим равенство
,
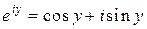которое называется формулой Эйлера.
Подставим в (2) вместо комплексно сопряженное число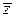 
:
(3) 
.
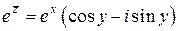Равенства (2) и (3) позволяют представить тригонометрические функци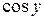и 
и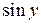 
от вещественной переменной , через функций комплексной переменно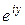й 
и 
:
(4) 
.
3) Тригонометрические функции и представляются равенствами
(5) 
,
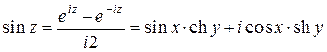(6) 
,
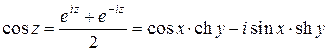где
– гиперболический косинус,
– гиперболический синус.
4) Тригонометрические функции 
и 
определяются как соответствующие вещественные функции:
.
5) Для гиперболических функций и получаются равенства
(7) 
,
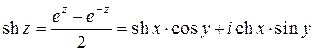(8) 
.
6) Логарифмическая функция 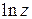определяется как обратная к показательной функции 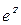. Как и многие обратные функции логарифмическая функция определяется неоднозначно:
(9) 
.
Значение, которое получается из (9) при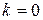 
:
(10) 
.
называется главным значением логарифма.
|
|
|
СВЯЗЬ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ И ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ
Имеют место равенства:
,
.
АНАЛИТИЧЕСКИЕ ФУНКЦИИ
Функция называется аналитической в области 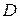, если она дифференцируема в каждой точке этой области.
Для исследования функции на аналитичность требуется выполнить следующие действия:
1) найти вещественную и мнимую части функции :
;
2) найти частные производные функций и :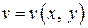
;
3) проверить выполнение условия Коши-Римана
в исследуемой области.
ГАРМОНИЧЕСКИЕ ФУНКЦИИ
Вещественная функция двух переменных называется гармонической в области 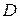, если она в этой области:
а) имеет непрерывные частные производные до второго порядка включительно;
б) удовлетворяет уравнению
(11) 
,
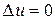где
(12) 
называется оператором Лапласа.
|
|
|
