 |
Сопряженные гармонические функции
|
|
|
|
Две гармонические функции двух переменных  и
и 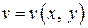 называются сопряженными гармоническими функциями в области
называются сопряженными гармоническими функциями в области 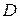 , если они удовлетворяю условиям Коши-Римана.
, если они удовлетворяю условиям Коши-Римана.
Если ФКП  аналитическая в области
аналитическая в области 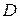 , то ее вещественная и мнимая части являются сопряженными гармоническими функциями в этой области.
, то ее вещественная и мнимая части являются сопряженными гармоническими функциями в этой области.
ВОССТАНОВЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ ПО
ЗАДАННОЙ ЕЕ ВЕЩЕСТВЕННОЙ ИЛИ МНИМОЙ ЧАСТИ
Для восстановления аналитической функции по заданной одной из ее частей необходимо выполнить следующие действия:
а) найти частные производные до второго порядка заданной функции двух переменных и проверить, что они удовлетворяют уравнению Лапласа;
б) найти сопряженную гармоническую функцию с помощью условий Коши-Римана;
в) записать ФКП 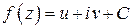 ; одна из функций
; одна из функций 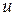 или
или  – заданная гармоническая функция, другая гармоническая функция найдена в пункте б), а
– заданная гармоническая функция, другая гармоническая функция найдена в пункте б), а 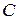 – произвольная постоянная;
– произвольная постоянная;
г) если задано значение искомой функции  в некоторой точке из области аналитичности, то необходимо найти значение постоянной
в некоторой точке из области аналитичности, то необходимо найти значение постоянной 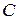
Задача 5
Дана функция комплексной переменной  и точка
и точка  . Вычислить
. Вычислить  и ответ представить в алгебраической форме.
и ответ представить в алгебраической форме.
| Задача 5 Образец |
 . .
|
Решение
Из Приложений 1 и 2 находим:
 ;
;


 .
.
Так как
 ,
,
то имеем

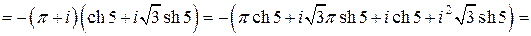
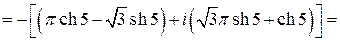
 .
.
Ответ: 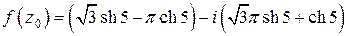
Задача 6
Дана функция комплексной переменной  . 1) определить действительную
. 1) определить действительную  и мнимую
и мнимую 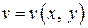 части функции
части функции  и 2) проверить выполнение условий Коши-Римана.
и 2) проверить выполнение условий Коши-Римана.
| Задача 6 Образец |
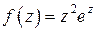 . .
|
Решение
Из Приложения 1 находим:
 ,
,
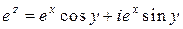 .
.
Тогда


 ;
;
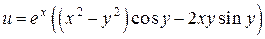 ,
,
 .
.
Найдем частные производные  и
и  :
:
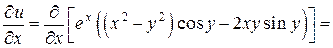


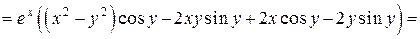
 ,
,
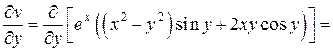

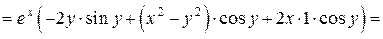

 .
.
Первое из условий Коши-Римана имеет место. Проверим второе:
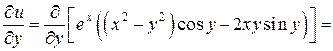



 ,
,



 .
.
Имеет место и второе из условий Коши-Римана.
Ответ: 1) 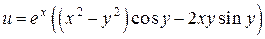 ,
,
|
|
|
 ;
;
2) имеют место условия Коши-Римана.
Задача 7
Проверить, что данная функция  является вещественной частью (
является вещественной частью (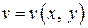 является мнимой частью) аналитической функции
является мнимой частью) аналитической функции  . Восстановить аналитическую функцию
. Восстановить аналитическую функцию  по данной функции
по данной функции  и
и  (по данной функции
(по данной функции 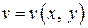 и
и 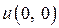 ).
).
| Задача 7 Образец |
 . .
|
Решение
Проверим гармоничность 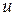 . Найдем частные производные
. Найдем частные производные  и
и 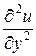 :
:
 ,
,
 ,
,
 ,
,
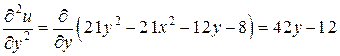 .
.
Так как
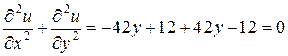 ,
,
то функция 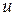 является гармонической. Найдем гармоническую сопряженную функцию
является гармонической. Найдем гармоническую сопряженную функцию  .
.
Из первого из условий Коши-Римана  получаем равенство
получаем равенство
 .
.
Интегрируем это равенство по  :
:
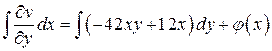 ,
,
где  – произвольная дифференцируемая функция. Отсюда
– произвольная дифференцируемая функция. Отсюда
 .
.
Вычислим 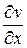 :
:
 .
.
Из второго из условий Коши-Римана  получаем равенство
получаем равенство
 ,
,
 ,
,
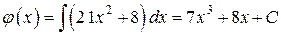 ,,
,,

где 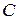 – произвольная постоянная. Согласно условию
– произвольная постоянная. Согласно условию 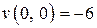 получаем, что
получаем, что  . Поэтому
. Поэтому
 .
.
Используя Приложение 1 найдем аналитическую функцию  :
:
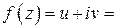


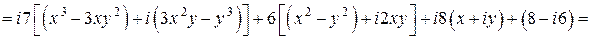
 .
.
Ответ:  .
.
Задача 8
С помощью операционного исчисления найти частное решение данного дифференциального уравнения с данными начальными условиями.
| Задача 8 Образец |
 . .
|
Решение
Используя свойства интегрального преобразования Лапласа, а также таблицу оригиналов и изображений (Приложение 3), найдем изображения по Лапласу всех элементов данной начальной задачи:
 ,
,
 ,
,

 .
.
Таким образом, изображение по Лапласу рассматриваемой начальной задачи имеет вид:
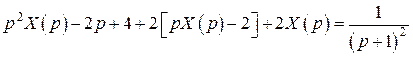 ,
,
 ,
,
 ,
,
 .
.
Используя метод неопределенных коэффициентов, разложим полученное операторное решение в сумму простейших дробей:
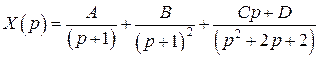



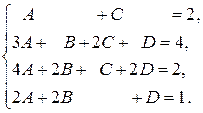 .
.
Решением полученной системы является:
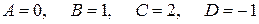 .
.
Переписав операторное решение с учетом найденных коэффициентов, получим
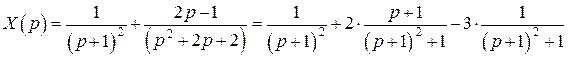 .
.
Используя таблицу изображений к оригиналов (Приложение 3), получим
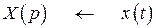 ,
,
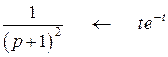 ,
,
 ,
,
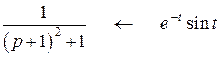 .
.
Подставим полученные оригиналы в операторное решение:
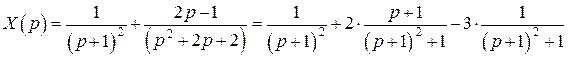 ,
,
 .
.
Ответ:  .
.
Задача 9
С помощью операционного исчисления найти частное решение данной системы дифференциальных уравнений соответствующее данными начальным условиям.
|
|
|
| Задача 9 Образец |
 . .
|
Решение
По таблице оригиналов и изображений (Приложение 3), будем иметь:
 ,
,
 ,
,

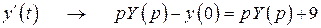
 .
.
Получим систему в изображениях:

 ,
,
Полученную систему линейных алгебраических уравнений относительно неизвестных  и
и  решим методом Крамера:
решим методом Крамера:
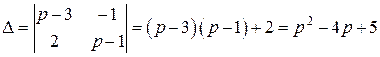 ,
,
 ,
,
 ,
,

Полученное операторное решение системы разложим в сумму простейших дробей:

 ,
,

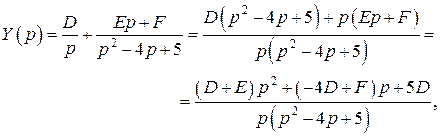
 ,
,

Искомыми разложениями являются:

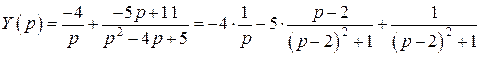 .
.
Найденным изображениям сопоставим их оригиналы (Приложения 3):
 ,
,
 ,
,
 .
.
Таким образом, нами получено искомое решение:
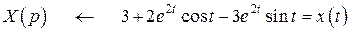 ,
,
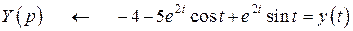 .
.
Ответ: 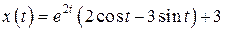 ,
,
 .
.
| Задача 10 Образец |
| Бросаются две игральные кости. Найти вероятность того, что сумма выпавших очков равна 8. |
Решение
Обозначим рассматриваемое событие буквой 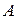 :
:
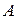 – «сумма выпавших очков равна 8».
– «сумма выпавших очков равна 8».
Вероятность  этого события находим по классической схеме:
этого события находим по классической схеме:
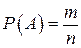 ,
,
где 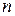 – число всех возможных исходов,
– число всех возможных исходов, 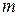 – число исходов, благоприятствующих появлению события
– число исходов, благоприятствующих появлению события 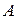 .
.
Число всех исходов равно 36: 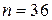 , а число благоприятствующих исходов равно 5:
, а число благоприятствующих исходов равно 5: 
 . Поэтому
. Поэтому
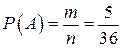 .
.
Ответ:  .
.
| Задача 11 Образец |
| Среди 9 лотерейных билетов 6 выигрышных. Наудачу взяли 3 билета. Найти вероятность того, что среди них 2 выигрышных. |
Решение
Обозначение:
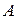 – «из 3 билетов 2 выигрышных».
– «из 3 билетов 2 выигрышных».
Три билета из числа 9 можно выбирать 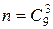 способами. Два выигрышных билета берут из числа 6:
способами. Два выигрышных билета берут из числа 6: 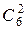 , а одного билета без выигрыша – из числа
, а одного билета без выигрыша – из числа  оставшихся билетов:
оставшихся билетов: 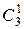 . Поэтому, число благоприятствующих исходов равно
. Поэтому, число благоприятствующих исходов равно 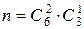 . Так как
. Так как
 ,
,
 ,
,
то
 .
.
Ответ: 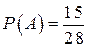 .
.
| Задача 12 Образец |
| Для первого стрелка вероятность попадания в мишень при одном выстреле равна 0,7, для второго – 0,8, а для третьего 0,6. Каждый стрелок сделал по одному выстрелу по мишени. Найти вероятность того, что в мишень попал: 1) только один стрелок; 2) хотя бы один стрелок. |
Решение
1) Обозначение:
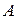 – «в мишень попал только один стрелок»,
– «в мишень попал только один стрелок»,
 – «в мишень попал
– «в мишень попал  -й стрелок»
-й стрелок»  .
.
Событии 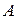 складывается из суммы трех несовместных событий:
складывается из суммы трех несовместных событий:
 .
.
В нашем случае:

Используя теорему о вероятности суммы несовместных событий и теорему о вероятности произведения независимых событий, получим


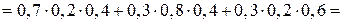
 .
.
Обозначение:
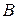 – «в мишень попал хотя бы один стрелок»,
– «в мишень попал хотя бы один стрелок»,
Вероятность появления хотя бы одного события удобно находить через вероятность противоположного события:
|
|
|
 ,
,
где  – «в мишень не попал ни один стрелок». Так как
– «в мишень не попал ни один стрелок». Так как  , то
, то
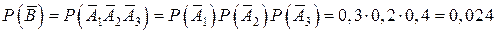 ,
,
 .
.
Ответ: 1)  ,
,
2) 
| Задача 13 Образец |
| Из 1000 ламп 230 принадлежат первой партии, 480 – второй партии и 290 – третьей партии. В первой партии 6% бракованных ламп, во второй – 5%, а в третьей – 4%. Наудачу выбирается одна лампе. Найти вероятность того, что выбранная лампа – бракованная. |
Решение
Обозначение:
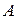 – «выбранная лампа – бракованная».
– «выбранная лампа – бракованная».
Искомую вероятность находим по формуле полной вероятности, рассчитанной на три гипотезы –  ,
,  ,
, 
 ,
,
где  – «выбранная лампа из
– «выбранная лампа из  -й партии»,
-й партии»,  – вероятность бракованной лампы в
– вероятность бракованной лампы в  -й партии
-й партии  . Так как
. Так как

то
 .
.
Ответ:  .
.
| Задача 14 Образец |
| Монету бросают 7 раз. Найти вероятность того, что герб выпал 2 раза. Найти наивероятнейшее число выпадений герба при 7 бросаниях монеты. |
Решение
Обозначение:
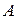 – «герб выпал 2 раза при 7 бросаниях монеты».
– «герб выпал 2 раза при 7 бросаниях монеты».
Вероятность  находится по формуле Бернулли
находится по формуле Бернулли
 ,
,
где  – вероятность выпадения герба при каждом бросании монеты,
– вероятность выпадения герба при каждом бросании монеты,  – вероятность выпадения цифры при каждом бросании монеты.
– вероятность выпадения цифры при каждом бросании монеты.
Так как  ,
,  ,
,  , то
, то
 .
.
Наивероятнейшее число 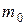 появлений события в
появлений события в 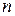 независимых испытаниях удовлетворяет двойному неравенству
независимых испытаниях удовлетворяет двойному неравенству
 .
.
В данном случае
 ,
,
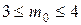 .
.
Если концы доверительного интервала являются целыми числами, то каждому из них соответствует наибольшее значение вероятности, рассчитываемой по формуле Бернулли.
Ответ:  ;
;
 .
.
| Задача 15 Образец | |||||||||
Дискретная случайная величина (ДСВ)  задана законом распределения, представленным в виде таблицы: задана законом распределения, представленным в виде таблицы:
| |||||||||

| 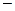 5 5
| 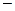 2 2
| 
| ||||||
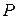
| 0,2 | 0,5 | 
| ||||||
Найти: 1)  ; 2) ; 2)  ; 3) ; 3) 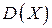 ; 4) ; 4)  , если , если  . Построить график функции распределения вероятностей . Построить график функции распределения вероятностей  . .
|
Решение
1) Так как сумма вероятностей в законе распределения вероятностей (сумма чисел во второй строке таблицы) равна 1, то
 .
.
2) По определению математическое ожидание 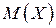 ДСВ
ДСВ  находится по формуле
находится по формуле
 .
.
В данном случае
 ,
,
 .
.
Таким образом, закон распределения вероятностей ДСВ  имеет следующий вид:
имеет следующий вид:

| 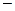 5 5
| 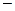 2 2
| 
| ||||||
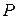
| 0,2 | 0,5 | 
|
|
|
|
3) По определению дисперсия 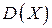 ДСВ
ДСВ  находится по формуле
находится по формуле
 .
.
В данном случае
 .
.
4) График функции распределения вероятностей ДСВ  легко можно построить, исходя из свойства этой функции: вероятность того, что ДСВ принимает одно из своих возможных значений, равно скачку функции распределения в соответствующей точке. Этот график приведен на следующем рисунке.
легко можно построить, исходя из свойства этой функции: вероятность того, что ДСВ принимает одно из своих возможных значений, равно скачку функции распределения в соответствующей точке. Этот график приведен на следующем рисунке.

Имея график функции распределения вероятностей, ее можно легко описать аналитически:
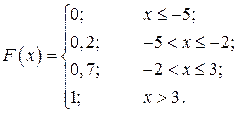
4) Вероятность  попадания ДСВ
попадания ДСВ  в интервал
в интервал  находится по
находится по
 .
.
В данном случае
 .
.
Ответ: 1) 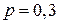 ,
,
2) 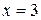 ,
,
3)  ,
,
4) 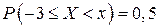 .
.
| Задача 16 Образец |
Непрерывная случайная величина (НСВ)  задана плотностью распределения вероятностей задана плотностью распределения вероятностей  : :
 где
где  .
Найти: 1) .
Найти: 1)  , 2) , 2)  – функцию распределения вероятностей; 3) – функцию распределения вероятностей; 3) 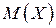 ; 4) ; 4) 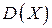 ; 5) ; 5)  . Построить графики плотности распределения и функцию распределения вероятностей. . Построить графики плотности распределения и функцию распределения вероятностей.
|
Решение
1) Значения параметра  находится из условия
находится из условия
 .
.
В данном случае:
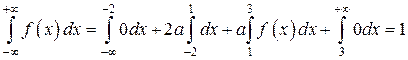 ,
,
 ,
,
 .
.
С учетом этого плотность распределения вероятностей НСВ  описывается следующим образом:
описывается следующим образом:
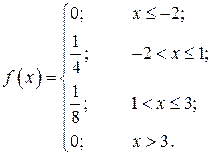
График плотности распределения представлен на следующем рисунке:

2) Функция распределения вероятностей НСВ  , заданной плотностью распределения
, заданной плотностью распределения  , вычисляется по формуле
, вычисляется по формуле
 .
.
Вычислим этот интеграл последовательно.
1)  :
:
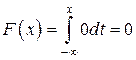 ;
;
2)  :
:
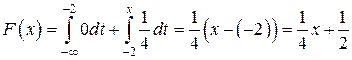 ;
;
3)  :
:
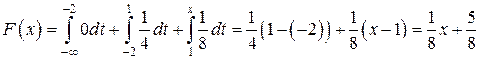 ;
;
4)  :
:
 .
.
Таким образом, функция распределения вероятностей НСВ  в данном случае имеет вид:
в данном случае имеет вид:
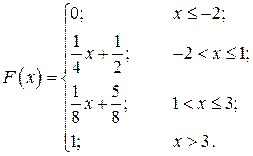
График функции распределения представлен на рисунке:
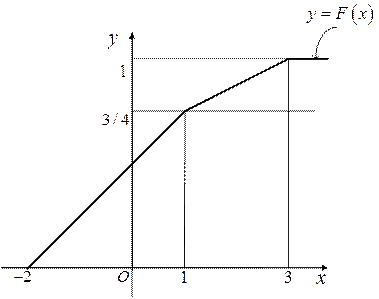
3) Математическое ожидание 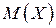 вычисляется по формуле
вычисляется по формуле
 .
.
В данном случае:

 .
.
4) Дисперсия 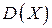 вычисляется по формуле
вычисляется по формуле
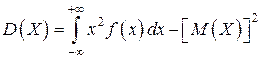 .
.
В данном случае:

 .
.
5) Вероятность попадания НСВ  в интервал
в интервал  вычислим двумя способами:
вычислим двумя способами:
 ,
,
 .
.
По первому способу:
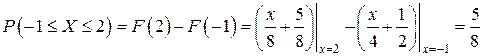 .
.
По первому способу:
 .
.
Ответ: 1)  ,
,
2) 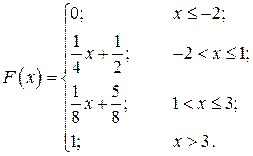 ,
,
3)  ,
,
4)  ,
,
5)  .
.
|
|
|


