Объекты нечисловой природы как статистические данные

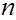       В математической статистике наиболее распространенный объект изучения - выборка  т.е. совокупность результатов наблюдений. В различных областях статистики результат наблюдения - это или число, или конечномерный вектор, или функция... Соответственно проводится деление математической статистики: одномерная статистика, многомерный статистический анализ, статистика временных рядов и случайных процессов... В статистике объектов нечисловой природы в качестве результатов наблюдений рассматриваются объекты нечисловой природы, в частности, перечисленных выше видов - измерения в шкалах, отличных от абсолютной, бинарные отношения, вектора из 0 и 1, множества, нечеткие множества. Выборка может состоять из ранжировок и 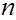 толерантностей, или  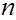множеств, или  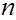нечетких множеств и т.д.

       Отметим необходимость развития методов статистической обработка "разнотипных данных", обусловленную большой ролью в прикладных исследованиях "признаков смешанной природы" [83]. Речь идет о том, что результат наблюдения состояния объекта зачастую представляет собой вектор, у которого часть координат измерена по шкале наименований, часть - по порядковой шкале, часть - по шкале интервалов и т.д. Статистические методы ориентированы обычно либо на абсолютную шкалу, либо на шкалу наименований (анализ таблиц сопряженности), а потому зачастую непригодны для обработки разнотипных данных. Есть и более сложные модели разнотипных данных, например, когда некоторые координаты вектора наблюдений описываются нечеткими множествами [43].

       Для обозначения подобных неклассических результатов наблюдений в 1979 г. [84] предложен собирательный термин - объекты нечисловой природы. Термин "нечисловой" означает, что структура [85] пространства, в котором лежат результаты наблюдений, не является структурой действительных чисел, векторов или функций, она вообще не является структурой линейного (векторного) пространства. При расчетах объекты числовой природы, разумеется, изображаются с помощью чисел.

       С целью "стандартизации математических орудий" [85, с.253] целесообразно разрабатывать методы статистического анализа данных, пригодные одновременно для всех перечисленных выше видов результатов наблюдений. Кроме того, в процессе развития прикладных исследований выявляется необходимость использования новых видов объектов нечисловой природы, отличных от рассмотренных выше, например, в связи с развитием статистических методов обработки текстовой информации [86].Поэтому целесообразно ввести еще один вид объектов нечисловой природы - объекты произвольной природы, т.е. элементы множества, на которые не наложено никаких условий (кроме "условий регулярности", необходимых для справедливости доказываемых теорем). Другими словами, в этом случае предполагается, что результаты наблюдений (элементы выборки) лежат в произвольном пространстве . Для получения теорем необходимо потребовать, чтобы  удовлетворяло некоторым условиям, например, было топологическим пространством. Как известно, ряд результатов математической статистики получен именно в такой постановке. Так, при изучении оценок максимального правдоподобия элементы выборки могут лежать в пространстве произвольной природы. Это не влияет на рассуждения, поскольку в них рассматривается лишь зависимость плотности вероятности от параметра. Методы классификации, использующие лишь расстояние между классифицируемыми объектами, могут применяться к совокупностям объектов произвольной природы, лишь бы в пространстве, где они лежат, была задана метрика. Цель статистики объектов нечисловой природы состоит в том, чтобы систематически рассматривать методы статистической обработки данных как произвольной природы, так и представляющих собой указанные выше конкретные виды объектов нечисловой природы, т.е. методы описания данных, оцениванию и проверки гипотез. Взгляд с общей точки зрения позволяет получить новые результаты и в других областях математической статистики.