 |
Данные опроса по оценке расходов на ЖКХ
|
|
|
|
Курзаева, Л.В.
К93 Введение в анализ данных с использованием информационных технологий: учеб.-метод. пособие / Л.В. Курзаева, И.Г. Овчинникова. – Магнитогорск: МаГУ, 2012. – 60 с.
Рассматриваются основные функциональные возможности табличных процессоров для анализа данных. В пособии приведены основные способы обработки данных на примере табличного процессора Microsoft Excel, а также раскрыты некоторые существенные отличия и особенности работы в Open Office.org Calc. Все способы и приемы работы с электронными таблицами рассмотрены на примерах. Пособие содержит краткие теоретические сведения, полезные для правильной интерпретации полученных результатов.
Данное пособие адресовано, прежде всего, студентам очной и заочной форм обучения, обучающимся по направлению подготовки «Социология» и будет полезно в ходе изучения дисциплины анализ данных, а также в рамках проведения самостоятельных исследований с использованием электронных таблиц.
© Магнитогорский государственный
университет, 2012

ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ........................................................................................................ 4
Построение таблиц одномерного распределения............ 5
1. Краткие теоретические сведения................................................................. 5
2. Использование Microsoft Excel и OpenOffice.org Calc при построении вариационных рядов................................................................................................................. 8
3. Задания для самостоятельной работы...................................................... 12
Вычисление характеристик рядов распределения........ 16
1. Краткие теоретические сведения............................................................... 16
2. Использование Microsoft Excel и OpenOffice.org Calc при вычислении выборочных характеристик................................................................................................ 23
|
|
|
3. Задания для самостоятельной работы...................................................... 26
Построение таблиц двухмерного распределения.......... 31
1. Краткие теоретические сведения............................................................... 31
2. Использование Microsoft Excel и OpenOffice.org Calc для построения таблиц двухмерного распределения......................................................................... 31
3. Задания для самостоятельной работы...................................................... 39
Анализ взаимосвязи количественных признаков......... 41
1. Краткие теоретические сведения............................................................... 41
2. Использование Microsoft Excel и OpenOffice.org Calc при анализе взаимосвязи количественных признаков............................................................................ 45
3. Задания для самостоятельной работы...................................................... 56
Список литературы.............................................................................. 60
ВВЕДЕНИЕ
Настоящее учебно-методическое пособие посвящено вопросам использования электронных таблиц при решении задач обработки, представления и основ анализа данных социологических исследований.
Для решения указанных задач имеется большое число различных математических методов, позволяющих полно и всесторонне обрабатывать, наглядно представлять и анализировать собранную информацию. В их поддержку разработан и активно используется большой арсенал программных средств математико-статистической обработки данных, среди которых можно выделить три большие типовые группы:
1. Табличные процессоры (электронные таблицы) – такие как Microsoft Office Excel, Open Office.org Calc, Lotus 1-2-3, QuattroPro.
2. Математические пакеты общего назначения – такие как MatLab, Mathсad.
3. Специализированные статистические пакеты – такие как Statistica, SPSS, STADIA, ДА-СИСТЕМА, Vortex.
Выбор в качестве объекта рассмотрения именно электронных таблиц обусловлен рядом причин.
Электронные таблицы наиболее просты в освоении по сравнению с другими программными средствами и при этом включают весь необходимый социологу инструментарий в достаточном для обработки, представления и анализа данных объеме. Выбранные же авторами Microsoft Office Excel и Open Office.org Calc имеют большую популярность по сравнению с другими табличными процессорами, а также математическими пакетами общего назначения и специализированными статистическими пакетами.
|
|
|
Кроме того, с дидактической точки зрения позволяют более подробно раскрыть суть и ход реализации методов компьютерной обработки данных.
Пособие включает теоретический материал и тренировочные задания, позволяющие ознакомиться с общими принципами, понятиями и методами обработки данных, а также получить представление и отработать навыки использования электронных таблиц.
Учебное пособие написано в соответствии с рабочей программой учебной дисциплины «Анализ данных в социологии». Для более углубленного изучения способов решения задач обработки, представления и анализа данных приводится список литературы.
Учебное пособие адресовано студентам, обучающимся по направлению подготовки «Социология», а также всем интересующимся проблемами обработки данных с использованием электронных таблиц.
Желаем успехов!
Построение таблиц
одномерного распределения
После изучения параграфа Вы научитесь строить ряды
распределения с использованием электронных таблиц.
1. Краткие теоретические сведения
Построение и дальнейший анализ одномерного распределения основывается на представлении данных в виде ряда распределения, который является исходным для применения большинства статистических методов.
Ряды распределения могут быть: атрибутивными, то есть построенными по признаку, т.е. измеренному в шкале качественного типа – номинальной или порядковой, и вариационными, то есть построенными по количественному признаку.
В зависимости от вида вариации ряд может быть дискретным или интервальным.
Дискретный вариационный ряд – это ряд, значения вариант которого выражены одним числом (значением признака).
Интервальный вариационный ряд это ряд, варианты которого выражены двумя числами (значениями признака), являющимися нижней и верхней границами интервала. Такие ряды обычно используются в случаях, когда число вариантов дискретного признака слишком велико, а также когда анализу подлежат вариации непрерывного признака. Интервалы в ряду могут быть как равными, так и неравными. Это зависит от характера статистических данных и задач исследования.
|
|
|
Вариационный ряд может быть асимметричным, т.е. таким, в котором наибольшей частотой обладают крайние значения вариант.
Частота – это величина, равная числу встречаемости признака в совокупности. Сумма частот равна количеству единиц наблюдения.
В социологии используются следующие разновидности частот:
Число опрошенных – сколько всего человек приняло участие в опросе, т.е. число ответивших и число не ответивших.
Число ответивших – сколько человек ответило на данный вопрос.
Число ответов – сколько ответов было дано на данный вопрос.
Число не ответивших – сколько человек не ответило на данный вопрос.
Частоты представляют собой абсолютный показатель распределения, а относительным показателем является частость (доля). Частость представляет собой отношение частоты встречаемости данного признака к сумме всех частот. Ее можно выражать как непосредственно в долях (тогда сумма частостей ряда будет равна единице), так и в процентах (тогда сумма частостей ряда будет равна 100%).
В социологии используются следующие виды процентов:
% от числа ответивших: единицей анализа в данном случае является человек, ответивший на данный вопрос, то есть не ответившие будут игнорироваться. За 100 % берется число ответивших.
% от числа опрошенных: рассчитывается для того, чтобы определить долю ответивших и не ответивших на данный вопрос. За 100% берется число опрошенных.
% от числа данных ответов: единицей анализа в данном случае выступает не человек, а его ответ. Здесь за 100 % выступает общее число данных ответов.
Примером дискретного ряда может служить распределение студентов по курсам:
| Курс | Количество студентов, чел. |
| 1-й | |
| 2-й | |
| 3-й | |
| 4-й | |
| 5-й | |
Графически эти данные можно отобразить в виде гистограммы (рис. 1).
|
|
|

Рис. 1. Гистограмма распределения количества студентов
по курсам (дискретный вариационный ряд)
Визуальный анализ гистограмм позволяет выявить характер распределения данных и ответить на следующие шесть вопросов:
1. Какие значения типичны для заданного набора данных?
2. Как различаются между собой значения (диапазон значений)?
3. Сконцентрированы ли данные вокруг некоторого типичного значения?
4. Какой характер имеет эта концентрация данных? В частности, одинаков ли характер «затухания» для малых и больших значений данных?
5. Есть ли в заданном наборе такие значения, которые сильно отличаются от остальных и требуют специальной обработки (выбросы, т.е. такие значения, которые либо слишком велики, либо слишком малы.)?
6. Можно ли сказать, что в целом это однородный набор или отчетливо наблюдается наличие групп, которые надо анализировать отдельно?
Интервальный ряд распределения – это ряд, в котором значения признака заданы в виде интервала. Например, распределение студентов по младшим и старшим курсам можно представить в виде интервального ряда:
| Курс | Количество студентов, чел. |
| 1–2-й | |
| 3–5-й | |
При этом графическое представление интервального ряда в виде гистограммы представлено на рис. 2.

Рис. 2. Гистограмма распределения количества студентов
по курсам (интервальный вариационный ряд)
При определении интервальных рядов распределения необходимо определить, какое число групп следует образовать и какие взять интервалы (равные, неравные, закрытые, открытые).
При установлении количества интервалов можно воспользоваться следующей формулой: r» [1+3,2 lg(n)], (r – количество интервалов, n – количество данных). Для того чтобы вариационный ряд не был слишком громоздким, обычно число интервалов берут от 6 до 11.
2. Использование Microsoft Excel и OpenOffice.org Calc
при построении вариационных рядов
Таблица 1
Функции Microsoft Excel и OpenOffice.org Calc,
используемые для построения вариационных рядов
| Функция Excel (рус.) | Функция Calc (англ.) | Назначение |
| МАКС | MAX | Возвращает максимальное значение из списка аргументов |
| МИН | MIN | Возвращает наименьшее значение в списке аргументов |
| ЧАСТОТА | FREQUENCY | Возвращает распределение частот в виде вертикального массива. В Excel имеет формат ЧАСТОТА (массив_данных;массив_интервалов), в Calc: FREQUENCY(массив_данных;массив_интервалов) Массив_данных – это массив или ссылка на множество данных, для которых вычисляются частоты. Массив_интервалов – это массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных» |
| LOG10 | LG | Возвращает значение десятичного логарифма |
|
|
|
Рассмотрим этапы построения вариационных рядов с использованием указанных функций на следующем примере.
Дана оценка расходов на ЖКХ 62 респондентов (табл. 2).
Таблица 2
Данные опроса по оценке расходов на ЖКХ
| № респондента | Оцените ваши расходы на ЖКХ за последний год | № респондента | Оцените ваши расходы на ЖКХ за последний год |
| - | |||
| № респондента | Оцените ваши расходы на ЖКХ за последний год | № респондента | Оцените ваши расходы на ЖКХ за последний год |
| - | |||
| - | |||
| - | |||
| - | |||
| - | - | ||
| - | |||
| - | |||
| - | |||
Этапы построения дискретного вариационного ряда
Заметим, что рассматриваемая далее последовательность шагов применима и для построения атрибутивного ряда, при условии предварительного кодирования данных (присваивания числовых аналогов нечисловым значениям признака).
Шаг 1. Подготовка данных – сортировка (данный шаг можно пропустить, т.к. он служит лишь для удобства восприятия ряда). Произведем сортировку по возрастанию представленных данных по столбцу «Оцените ваши расходы на ЖКХ за последний год».
Для этого выделите весь диапазон данных, выберите в пункте меню Сервис опцию Сортировка, а затем в открывшемся окне установите столбец, по которому будет производиться сортировка и вид сортировки – по возрастанию.
После сортировки данные будут выглядеть как на рис. 3, при этом в конце ряда останутся респонденты, не ответившие на вопрос (ответы отмечены знаком «-»).
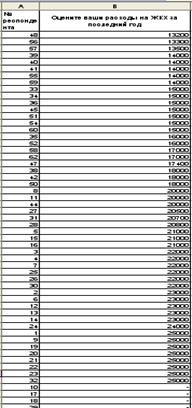

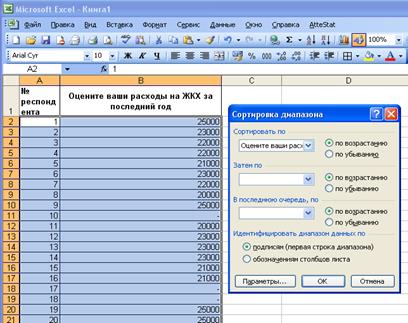
Рис. 3. Сортировка данных
Шаг 2. Построение массива признаков. Данный шаг можно осуществить двумя способами.
1 способ: ручной ввод. Выписать по одному все встречающиеся значения исследуемого признака (например, в столбец D). Этот способ прост в том случае, если данные были отсортированы (шаг 1), но и это при большом объеме данных не позволяет избежать ошибок, а также затрачивает достаточно много времени.
2 способ: автоматический. Выбираем в меню Данные и в нем Фильтр – Расширенный фильтр. В открывшемся окне (см. рис. 4) устанавливаем переключатель на положение Скопировать результат в другое место, указываем интересующий нас интервал сходных данных в поле Исходный диапазон; указываем ячейку – место начала размещения массива признаков в окне Переместить результат в диапазон, устанавливаем флажок Только уникальные записи. Этот способ более предпочтителен.
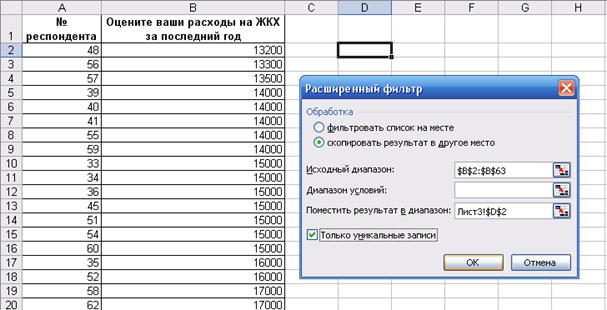
Рис. 4. Расширенный фильтр
Шаг 3. Расчет частот. Теперь выделите весь диапазон ячеек напротив выделенных признаков (например, Е2:Е19), поставьте знак «=», укажите имя функции ЧАСТОТА, после открывающихся скобок выделите массив_данных (D2:D63), а затем через точку запятой массив_интервалов – значения исследуемого признака (D2:D19). После закрытия скобок нажмите удерживая Ctrl+Shift кнопку Enter (такая комбинация клавиш для ввода функций используется всегда при работе с массивами данных).
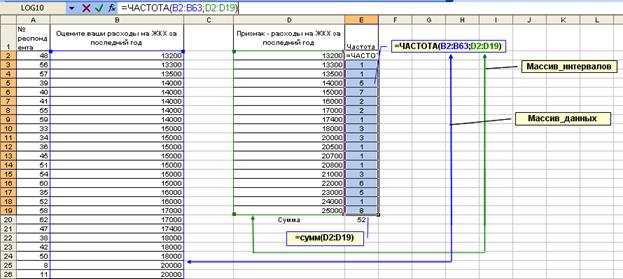
Рис. 5. Использование функции ЧАСТОТА
Как видно на рис. 5, сумма всех частот равна 52, а всего было опрошено 62 респондента. Разница между количеством опрошенных и ответивших составляет как раз 10 человек. Самостоятельно рассчитайте проценты от опрошенных, от ответивших и постройте гистограммы.
Этапы построения интервального вариационного ряда
Так как дискретный вариационный ряд из нашего примера содержит довольно большое число значений признака (18 значений признаков), было бы более правильно представить исходные данные в виде интервального ряда. Рассмотрим шаги построения последнего.
Шаг 1. Определение количества интервалов. Воспользовавшись формулой Стержеса, вычислим рекомендуемое количество интервалов: r»1+3,2*lg(n)»1+3,2*lg(62)»6,7. Округлив полученное значение до целых, определяем, что ряд будет содержать 7 интервалов (ячейка Е1 на рис. 6).
Шаг 2. Определение шага (длины интервала). Для того чтобы интервалы ряда были равными, вычислим шаг следующим образом: определим разность между максимальным и минимальным значениями в исходном ряду данных, а затем разделим ее на количество интервалов (ячейка E2 на рис. 6).
Шаг 3. Восстановление массива интервалов. Теперь, начиная от минимального значения исходных данных, с учетом вычисленной длины интервалов, создадим массив интервалов (диапазон ячеек D5:D12 на рис. 6).
Шаг 4. Расчет частот. Расчет частот производится с помощью функции ЧАСТОТА так же, как и в случае дискретного ряда (см. шаг 3 в этапах построения дискретного ряда), при этом в качестве массива интервалов используются конечные значения рассчитанных интервалов (диапазон ячеек D6:D12 на рис. 6).
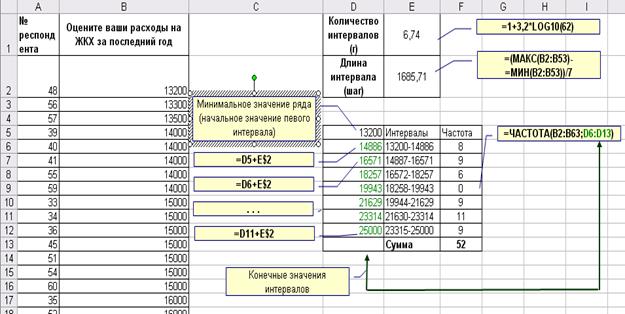
Рис. 6. Построение интервального ряда
3. Задания для самостоятельной работы
Задание 1
В ходе опроса политической активности мужского и женского населения, задавался вопрос: «Оцените по 3-х бальной системе свою активность» (3 – не интересуюсь политикой вовсе, 2 – средняя заинтересованность, 1 – интересуюсь и участвую в политической жизни).
Результаты ответов представлены в табл. 3.
Таблица 3
Распределение ответов
| Номер респондента- мужчины | Ответ | Номер респондента- женщины | Ответ |
| - | |||
| - | |||
Необходимо построить вариационный ряд, определить частоту, процент от опрошенных, от ответивших.
Задание 2
Институтом высоких статистических технологий и эконометрики в 1994 г. (табл. 4). В первом столбце приведены номера экспертов, в остальных четырех – четыре прогнозных значения, полученных от каждого эксперта. Орлов А.И.
Прикладная статистика
М.: Издательство «Экзамен», 2004.
Таблица 4[1]
|
|
|


