Прогнозы экспертов на 8 декабря 1994 г. (сделаны 19.10.1994)

№ п/п	Курс доллара США, руб.	Инфляция (%) за период прогноза	Цена батона белого хлеба, руб.	Цена 1 л молока, руб.
		4,0 2,8 17,0 16,0 16,0 5,0 3,5 62,0 54,0 10,0 54,0 54,0 9,0 54,0 40,0 13,0 15,0 2,5 200,0 6,0 3,0 12,0 11,0 54,0 62,0 73,0 54,0 38,0 38,0 38,0 2,0 46,0 92,0

 

Для лучшего восприятия прогнозов экспертов о цене 1 л молока составьте дискретный и интервальный вариационные ряды. Рассчитайте проценты от опрошенных, от ответивших.

Задание 3

Для лучшего восприятия прогнозов экспертов о цене 1 батона белого хлеба составьте дискретный и интервальный вариационные ряды по данным задания 2. Рассчитайте проценты от опрошенных, от ответивших.

 

Задание 4

Для лучшего восприятия прогнозов экспертов об инфляции составьте дискретный и интервальный вариационные ряды по данным задания 2. Рассчитайте проценты от опрошенных, от ответивших.

Задание 5

Для лучшего восприятия прогнозов экспертов о курсе доллара составьте дискретный и интервальный вариационные ряды по данным задания 2. Рассчитайте проценты от опрошенных, от ответивших.

Вычисление характеристик рядов распределения

После изучения параграфа Вы научитесь производить анализ данных
с использованием описательной статистики на основе пакета анализа
и специальных функции.

1. Краткие теоретические сведения

Описательная статистикаохватывает методы описания статистических данных, представления их в форме рядов распределений.

Условно все характеристики рядов распределения можно разделить на четыре группы:

1. Показатели, характеризующие закон распределения.

2. Показатели, характеризующие центральную тенденцию (меры среднего уровня).

3. Показатели (меры), характеризующие рассеяние относительно центральной тенденции.

4. Показатели асимметрии.

Рассмотрим их подробнее.

Показатели, характеризующие закон распределения. Это, прежде всего, уже знакомые нам частоты и проценты, а также накопленные частоты и проценты.

Как для абсолютных, так и для относительных частот можно определить кумулятивные показатели – накопленные частоты и проценты, которые рассчитывается путем суммирования всех частот (процентов) до выбранной категории включительно.

Упомянем также квартили, разбивающие ранжированный ряд значений признака на 4 части по 25% значений в каждой. Квартили при этом называются нижней, средней и верхней (при этом, очевидно, средняя квартиль совпадает с медианой). Аналогично можно ввести децили, разбивающие вариационный ряд значений на группы по 10% чисел и другие квантили – числа, разбивающие упорядоченную совокупность значений признака на равные по объему части.

Показатели, характеризующие центральную тенденцию (меры среднего уровня). Средняя представляет собой количественную характеристику качественно однородной совокупности. Наиболее распространенными средними являются средняя арифметическая, мода и медиана.

Средняя арифметическая () – обобщающий показатель, выражающий типичные размеры количественных признаков качественно однородных явлений, определяется по формуле:

,

где x_i – варианта с порядковым номером ( =1,… n); n – объем совокупности.

Для интервального ряда используется средняя арифметическая взвешенная:

,

где f_i – частота индивидуального значения признака;

k – количество градаций признака.

 

Мода () – варианта, которая чаще всего встречается в данном вариационном ряду. В интервальном ряду по определению можно установить только модальный интервал, при этом значение моды определяется по формуле:

,

где x₀ – нижняя граница модального интервала;

l – величина интервала;

f _μo – частота модального интервала;

f _μo–1 – частота предмодального интервала;

f _μo+1 – частота послемодального интервала.

Медиана () – варианта, находящаяся в середине вариационного ряда:

= , если число вариант нечетно (n =2 m +1);

= , если число вариант четно (n =2 m).

Медиана используется, когда изучаемая совокупность неоднородна. Особое значение она приобретает при анализе асимметричных рядов – она дает более верное представление о среднем значении признака, т.к. не столь чувствительна к крайним (нетипичным в плане постановки задачи) значениям, как средняя арифметическая.

Для интервального ряда можно определить как медианный интервал, а сама медиана рассчитывается по формуле:

,

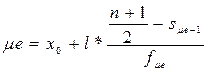где x ₀ – нижняя граница медианного интервала;

l – величина интервала;

n – количество единиц в совокупности;

s _{μe– 1} – накопленная частота предмедианного интервала;

f _μe – частота медианного интервала.

 

Показатели (меры), характеризующие рассеяние относительно центральной тенденции. Средние позволяют охарактеризовать статистическую совокупность одним числом, однако, не содержат информации о том, насколько хорошо они представляют эту совокупность. Для определения того, насколько сильно варьируются значения признака, используются такие характеристики, как размах вариации, дисперсия и среднее квадратическое отклонение.

Все они показывают, насколько сильно варьируют значения признака (а точнее – их отклонения от среднего) в данной совокупности. Чем меньше значение меры разброса, тем ближе значения признака у всех объектов к своему среднему значению, а значит, и друг к другу. Если величина меры разброса равна нулю, значения признака у всех объектов одинаковы.

Размах вариации (R) – это разность между наибольшим и наименьшим значениями признака:

,

где x_max – максимальное значение признака;

x_min – минимальное значение признака.

Показатель этот достаточно просто рассчитывается, однако является наиболее грубым из всех мер рассеяния, поскольку при его определении используются лишь крайние значения признака, а все другие просто не учитываются.

При расчете двух других характеристик меры вариации признака используются отклонения всех вариант от средней арифметической. Эти характеристики (дисперсия и среднее квадратическое отклонение) нашли самое широкое применение почти во всех разделах математической статистики.

Дисперсия (s ²) – абсолютная мера вариации (колеблемости) признака в статистическом ряду – средний квадрат отклонения всех значений признака ряда от средней арифметической этого ряда:

,

где x_i – варианта с порядковым номером ;

– средняя арифметическая;

n – объем совокупности.

Дисперсия для вариационного ряда рассчитывается по формуле:

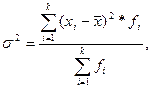
где – среднее значение признака;

x_i – индивидуальное значение признака;

f_i – общее число единиц наблюдения.

 

Для качественных шкал рассчитывается дисперсия доли. При наличии двух взаимоисключающих вариантов значений признака говорят о наличии альтернативной изменчивости качественного признака. Эквивалентом такого признака будет переменная, которая принимает значение 1, если обследуемая единица обладает данным признаком, и значение 0, если обследуемая единица не обладает им. К такому виду можно привести любую переменную, выделив группу единиц, обладающих данным значением признака, и группу единиц, обладающих всеми остальными значениями признака. Тогда дисперсия доли будет рассчитана по формуле:

,

где p – доля единиц, обладающих данным значением признака

 

Дисперсия применяется как для оценки рассеяния признака, так и для определения ошибки репрезентативности.

Дисперсия выражает разброс в «единицах в квадрате» (например, в «рублей в квадрате»). Для представления меры вариации в тех же единицах, что и варианты, используется среднее квадратическое (стандартное) отклонение, которое интерпретировать гораздо проще, т.к. выражается в привычных для нас единицах (например, в «рублях»).

Среднее квадратическое (стандартное) отклонение (s) – это квадратный корень из дисперсии:

или .

Стандартное отклонение показывает, насколько в среднем индивидуальные значения признака отличаются от среднего.

В случае, когда набор данных имеет нормальное распределение, стандартное отклонение приобретает особый смысл. На рис. 7 по обе стороны от среднего сделаны отметки на расстоянии одного, двух и трех стандартных отклонений соответственно. Так, примерно 66,7% (две трети) всех значений находятся в пределах одного стандартного отклонения по обе стороны от среднего значения, 95% значений окажутся в пределах двух стандартных отклонений от среднего и почти все данные (99,7%) будут находиться в пределах трех стандартных отклонений от среднего значения. Это свойство стандартного отклонения для нормально распределенных данных называется «правилом двух третей».

 

 

Рис. 7. Свойство стандартного отклонения для нормально распределенных данных

Приведенные выше формулы предназначены для расчета стандартного отклонения по генеральной совокупности. При расчете стандартного отклонения выборочной совокупности (обозначается символом s) производят деление на n–1. Следовательно, величина выборочного стандартного отклонения получается несколько больше, что обеспечивает поправку на случайность самой выборки.

Рассмотренные меры рассеяния – абсолютные величины. Однако часто бывает необходимо сравнить вариацию одного и того же признака у разных групп объектов, выявить степень различия одного и того же признака у одной и той же группы объектов в разное время, сопоставить вариацию разных признаков у одних и тех же групп объектов. Для решения этих задач необходимо использовать относительные показатели. Таким показателем является коэффициент вариации.

Коэффициент вариации (V) – это отношение стандартного отклонения к средней арифметической, выраженное в процентах:

.

Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).

Коэффициент вариации часто используют при проведении сравнений выборок различных объемов.

Следует отметить, что при ассиметричном (скошенном) распределении данных коэффициент вариации может превысить 100%. Такой результат означает, что в изучаемой ситуации наблюдается очень сильный разброс данных относительно среднего.

Показатели асимметрии. В рамках данной группы показателей выделим коэффициенты асимметрии и эксцесса.

Асимметрия – показатель, отражающий перекос распределения относительно среднего арифметического влево или вправо. В тех случаях, когда какие-нибудь причины благоприятствуют более частому появлению значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения. При левосторон­ней, или положительной, асимметрии в распределении чаще встречаются более низкие значения признака, а при правосторонней, или отрица­тельной – более высокие.

.

Сильная асимметрия встречается в специфических выборках. Если мы возьмем учеников-отличников и измерим IQ, то вероятно получим распределение, скошенное вправо (в сторону высоких баллов).

Эксцесс – показатель, отражающий высоту распределения. В тех случаях, когда какие-либо причины способствуют преимущественному появлению средних или близких к средним значений, образуется распределение с положительным эксцессом. Если же в распределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двувершинное.

.

Выбор показателей зависит от исследовательских задач и от уровня, на котором замерен признак. Для шкал более высокого уровня можно использовать все показатели, которые используются для шкал более низкого уровня, но не все показатели, используемые для шкал более высокого уровня можно использовать для шкал более низкого уровня (табл. 5).

Таблица 5

Примеры использования статистических методов в зависимости от шкалы измерения

Шкала	Тип	Основные эмпирические операции	Типичные примеры	Показатели закона распределения	Меры положения «центральной тенденции»	Меры рассеяния относительно центральной тенденции
Наименований (номинальная)	Качественные	Установление равенства	Нумерация игроков футбольной команды	Частоты, проценты	Мода	Дисперсия доли
Порядковая (ординальная)	Установление отношений (больше – меньше)	Ранжирование лиц по признаку (лучше – хуже)	Частоты, проценты	Мода, медиана	Дисперсия доли
Интервальная	Количественные	Установление равенства интервалов	Температура по Цельсию или Фаренгейту, энергия, календарные даты	Частоты, проценты, накопленные частоты	Мода, медиана, средняя арифметическая	Размах вариации, стандартное отклонение, коэффициент вариации
Отношений	Установление равенства отношений	Длина, вес, сопротивление, шкала высоты звука, шкала громкости звука	Частоты, проценты, накопленные частоты	Мода, медиана, средняя арифметическая, средняя гармоническая, средняя геометрическая	Те же

2. Использование Microsoft Excel и OpenOffice.org Calc
при вычислении выборочных характеристик

2.1. Использование инструмента Пакет анализа в Microsoft Excel

В пакете Microsoft Excel помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками и углубленного анализа данных, называемый «Пакет анализа», который может быть использован для решения задач обработки выборочных данных.

Для установки пакета Анализ данных в Microsoft Excel сделайте следующее:

– в меню Сервис выберите команду Надстройки;

– в появившемся списке установите флажок Пакет анализа.

Рассмотрим этапы вычисления основных показателей описательной статистики средствами «Пакета анализа» на следующем учебном примере (довольно красноречивом с точки зрения рассмотрения применения рассмотренных выше показателей вариационного ряда).

На рис. 8 приведены данные по стоимости товара N по двум странам (в условных единицах).

Рис. 8. Исходные данные

Шаг 1. Выберите пункт меню Сервис и опцию Анализ данных (если команда Анализ данных отсутствует в меню Сервис, то необходимо установить в Microsoft Excel пакет анализа данных). В появившемся окне (рис. 9) выберите строку Описательная статистика и нажать кнопку ОК.

Рис. 9. Окно пакета «Анализ данных»

Шаг 2. В диалоговом окне Описательная статистика (рис. 10):

· укажите входной интервал – ссылки на ячейки, содержащие анализируемые данные;

· установите флажок в поле Метка в первой строке (если входной интервал включает заголовки столбцов);

· в разделе Группирование переключатель установите в положение по столбцам (так как наши данные расположены по странам в столбцах);

· указать выходной интервал – ссылку на ячейку, в которую будут выведены результаты анализа;

· установите флажок в поле Итоговая статистика (для того чтобы отчет содержал расчеты средней арифметической, моду, медианы, стандартного отклонения, дисперсии и др. характеристик) и Уровень надежности нажать ОК.

Рис. 10. Окно «Описательная статистика»

После нажатия кнопки ОК Microsoft Excel представит отчет следующего вида (рис. 11).

Рис. 11. Отчет описательной статистики

Интерпретируем полученные данные.

На основании проведенного выборочного исследования и рассчитанных по данной выборке показателей описательной статистики с уровнем надежности 95% можно предположить, что средняя стоимость товара N в Стране 1 на протяжении 10 лет варьировалась в пределах от 0 до 169,85 рублей. Данный вывод обусловлен значениями средней арифметической выборки и предельной ошибкой выборки (показатель Уровень надежности (95,0%)), которые определяют границы варьирования генеральной средней следующим соотношением

,

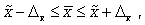где – генеральная и выборочная средние соответственно;

– предельная ошибка выборки.

Такой большой разброс (и несостоятельность выбора средней арифметической в качестве средней меры по данным Страны 1) подтверждается как значительным отклонением от медианы, так и рассчитанным значением стандартного отклонения. При этом коэффициент вариации (рассчитайте его самостоятельно на основе данных отчета) существенно превышает 33 %, что свидетельствует о неоднородности ряда и существенной колеблемости признака. Значительные положительные значения коэффициента асимметрии и эксцесс позволяют говорить о том, что данное распределение существенно отличается от нормального. Все это говорит о целесообразности выбора в качестве средней меры медианы.

Кардинально иная картина складывается по Стране 2. Попробуйте самостоятельно сделать соответствующие выводы.

2.2. Использование специальных функций

Ниже в табл. 6 приведены специальные функции анализа данных, используемые в рамках описательной статистики.

Таблица 6

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: