 |
Общий вид таблицы двух признаков
|
|
|
|
| Признак Y | Признак X | Всего | |||||
| x1 | x2 | … | xj | … | xk | ||
| y1 | f11 | f12 | … | f1j | … | f1m | n1 |
| y2 | f21 | f22 | … | f2j | … | f2m | n2 |
| … | … | … | … | … | … | … | … |
| yi | fi1 | fi2 | … | fij | … | fim | ni |
| … | … | … | … | … | … | … | … |
| ym | fk1 | fk2 | … | fkj | … | fm | nm |
| Итого | n1 | n2 | … | nj | … | nk | n |
В этой таблице:
fij – обозначения внутриклеточных частот, т.е. значение количества совместно встречающихся в совокупности i -го значения Y и j -го значения X.
ni – маргиналы (итоговые частоты) по Y показывают, сколько раз в совокупности встречается i -е значение Y.
nj – маргиналы (итоговые частоты) по X, показывают, сколько раз в совокупности встречается j -е значение X.
N – объем изучаемой совокупности.
2. Использование Microsoft Excel и OpenOffice.org Calc
для построения таблиц двухмерного распределения
Построение двумерного распределения в обоих средствах осуществляется с помощью инструмента Сводная таблица (меню Данные – опция Сводная таблица).Этот же инструмент может быть использован и для построения одномерных таблиц распределения – вариационных рядов.
Рассмотрим этапы построения сводных таблиц на следующем примере. В ходе опроса 38 респондентов были получены данные относительно их возраста и семейного положения.
Таблица 10
Данные опроса
| № респондента | Возраст (полных лет) | Семейное положение | № респондента | Возраст (полных лет) | Семейное положение |
| холост(ая) | холост(ая) | ||||
| холост(ая) | женат (замужем) | ||||
| холост(ая) | холост(ая) | ||||
| холост(ая) | холост(ая) | ||||
| холост(ая) | женат (замужем) | ||||
| холост(ая) | разведен(а) | ||||
| холост(ая) | холост(ая) | ||||
| холост(ая) | холост(ая) | ||||
| холост(ая) | холост(ая) | ||||
| холост(ая) | холост(ая) | ||||
| женат (замужем) | холост(ая) | ||||
| холост(ая) | женат (замужем) | ||||
| разведен(а) | холост(ая) | ||||
| холост(ая) | холост(ая) | ||||
| холост(ая) | холост(ая) | ||||
| холост(ая) | женат (замужем) | ||||
| разведен(а) | холост(ая) | ||||
| холост(ая) | разведен(а) |
Шаг 1. Выбор источника данных для сводной таблицы и вида создаваемого отчета (рис. 12).
|
|
|

Рис. 12. Шаг 1 Мастера сводных диаграмм MS Excel
Шаг 2. Укажите диапазон данных, подлежащих учету при построении сводной таблицы (диапазон данных задается вместе с заголовками столбцов) как на рис. 13.

Рис. 13. Шаг 2 Мастера сводных диаграмм MS Excel
Шаг 3. Укажите место, где будет размещаться сводная таблица и нажмите кнопку Готово (рис. 14).

Рис. 14. Шаг 3 Мастера сводных диаграмм MS Excel
Шаг 4. В появившийся макет сводной таблицы перетащите элементы из Списка полей сводной таблицы (рис. 15).
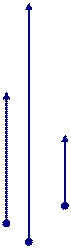

Рис. 15. Работа с макетом сводной таблицы
Шаг 5. Вычисление поля сводной таблицы осуществляется по умолчанию посредством суммирования. Но так как в данных у нас находятся номера респондентов, то вычисление должно осуществляться посредством счета количества респондентов (т.е. внутриклеточных частот).Для этого в панели сводной таблице нужно выбрать опцию Параметры поля. В открывшимся окне (рис. 16) выберите операцию Количество и нажмите кнопку ОК.

Рис. 16. Вычисление полей сводной таблицы
Основные приемы работы с данными в сводной таблице
2.1. Группировка данных
В рассматриваемом примере признак «Ваш возраст (полных лет)» можно для удобства дальнейшего анализа представить в виде интервалов. Для этого, вызвав контекстное меню нажатием правой кнопки мыши по серому полю «Ваш возраст (полных лет)» в сводной таблице, нужно выбрать опцию Группа и структура – Группировать…
|
|
|
В появившемся окне (см. рис. 17) необходимо установить запрашиваемые параметры – начальное и конечное значения группировки и шаг.

Рис. 17.Окно « Группирование»
Тогда исходная таблица примет вид, как на рис. 18.

Рис. 18. Результаты группировки
2.2. Дополнительные вычисления в сводных таблицах
Сводные таблицы предлагают большие возможности для дополнительных расчетов. Продемонстрируем это на примере расчета процентов по строкам. Для этого вызовем уже знакомое нам окно Вычисление поля сводной таблицы.
Нажмите на кнопку Дополнительно>>. В списке Дополнительные вычисления выберите нужную операцию – Доля от суммы по строке (рис. 19).

Рис. 19. Вычисление полей сводной таблицы
После нажатия на кнопку ОК таблица преобразуется и примет вид как на рис. 20.

Рис. 20. Результат дополнительных вычислений
2.3. Построение диаграмм
На панели сводной таблицы выберите опцию Мастер диаграмм, который сразу же на отдельном листе представит диаграмму (рис. 21). Нажав еще раз иконку Мастера диаграммы, можно изменить ее вид, добавить подписи данных и пр.


Рис. 21. Диаграмма, построенная на основе сводной таблицы
В OpenOffice.org Calc построение и работа со сводной таблицей основывается на тех же принципах, что и в Microsoft Excel. Вкратце обозначим ход работы.
Шаг 1. Выделите данные, подлежащие обработке в сводной таблице, и в меню Данные выберите опцию Сводная таблица. В открывшемся окне нажатием кнопки OK подтвердите, что обработке подлежат текущие данные (рис. 22).

Рис. 22. Выбор источника данных для построения сводной таблицы
Шаг 2. Перетащите поля данных на соответствующие поля разметки и определите, куда будет выведен результат (рис. 23).


Рис. 23. Работа с разметкой сводной таблицы
Нажав кнопку Параметры…, выберите в поле Функция – «Количество». Дополнительно можно выбрать тип отображаемого значения, например «% от строк» (рис. 24). После нажатия на кнопку ОК сформируется запрашиваемая таблица.

Рис. 24. Вычисление полей данных
3. Задания для самостоятельной работы
Задание 1
Постройте таблицу двухмерного распределения по данным столбцов «Возраст (полных лет)» и «Заработная плата в прошлом месяце» (см. табл. 8). Рассчитайте проценты по строкам и столбцам. Произведите необходимые, на ваш взгляд, дополнительные вычисления и постройте наиболее подходящие диаграммы. Интерпретируйте полученные результаты.
|
|
|
Задание 2
Постройте таблицу двухмерного распределения по данным столбцов «Семейное положение» и «Заработная плата в прошлом месяце» (см. табл. 8). Рассчитайте проценты по строкам и столбцам. Произведите необходимые, на ваш взгляд, дополнительные вычисления и постройте наиболее подходящие диаграммы. Интерпретируйте полученные результаты.
Задание 3
Постройте таблицу двухмерного распределения по данным столбцов «Плата за свет в прошлом месяце» и «Заработная плата в прошлом месяце» (см. табл. 8). Рассчитайте проценты по строкам и столбцам. Произведите необходимые, на ваш взгляд, дополнительные вычисления и постройте наиболее подходящие диаграммы. Интерпретируйте полученные результаты.
Задание 4
Постройте таблицу двухмерного распределения по данным столбцов «Плата за свет в прошлом месяце» и «Возраст (полных лет)» (см. табл. 8). Рассчитайте проценты по строкам и столбцам. Произведите необходимые, на ваш взгляд, дополнительные вычисления и постройте наиболее подходящие диаграммы. Интерпретируйте полученные результаты.
Задание 5
Постройте таблицы одномерного распределения по данным столбцов табл. 8 «Плата за свет в прошлом месяце» и «Возраст (полных лет)» (предварительного кодирования данных не требуется). Произведите необходимые, на ваш взгляд, дополнительные вычисления и постройте наиболее подходящие диаграммы. Интерпретируйте полученные результаты.
Задание 6
Постройте таблицу двухмерного распределения по данным таблицы 11.
Таблица 11[2]
Данные по странам за 1999 г. об ожидаемой продолжительности
жизни и суточной калорийности питания населения
| Страна | Ожидаемая продолжительность жизни при рождении в 1999 г., лет | Суточная калорийность питания населения, ккал на душу |
| Бельгия | 77,2 | |
| Бразилия | 66,8 | |
| Великобритания | 77,2 | |
| Венгрия | 70,9 | |
| Германия | 77,2 | |
| Греция | 78,1 | |
| Дания | 75,7 | |
| Египет | 66,3 | |
| Израиль | 77,8 | |
| Индия | 62,6 | |
| Испания | 78,0 | |
| Италия | 78,2 | |
| Канада | 79,0 | |
| Казахстан | 67,7 | |
| Китай | 69,8 | |
| Латвия | 68,4 | |
| Нидерланды | 77,9 | |
| Норвегия | 78,1 | |
| Польша | 72,5 | |
| Республика Корея | 72,4 | |
| Россия | 66,6 | |
| Румыния | 69,9 | |
| США | 76,6 | |
| Турция | 69,0 | |
| Украина | 68,8 | |
| Финляндия | 76,8 | |
| Франция | 78,1 | |
| Чехия | 73,9 | |
| Швейцария | 78,6 | |
| Швеция | 78,5 | |
| ЮАР | 64,1 | |
| Япония | 80,0 |
|
|
|
Анализ взаимосвязи количественных признаков
После изучения параграфа определять силу, направление
и форму взаимосвязи количественных признаков
1. Краткие теоретические сведения
Анализ взаимосвязи признаков производится в рамках решения тре основных задач:
1. Описание и понимание взаимосвязи.
2. Прогнозирование и предсказание нового наблюдения.
3. Корректировка и управление процессом.
Существует два вида анализа двумерных данных, представленных переменными X и Y: корреляционный анализ, позволяющий оценить степень взаимосвязи между переменными X и Y, и регрессионный анализ, определяющий форму связи между этими переменными.
Корреляция – это взаимосвязь количественных или порядковых признаков.
Интерпретация корреляции проводится на основании:
1) коэффициента корреляции (r) и его квадрата – коэффициент детерминации (R2), которые свидетельствуют о силе связи; R2 представляет собой долю вариации, общую для двух переменных (иными словами, "степень" зависимости или связанности двух переменных);
2) уровня значимости, вычисленного для каждого коэффициента корреляции, позволяющего судить о надежности корреляции;
3) визуального анализа связи.
Коэффициент корреляции – мера, показывающая, в какой степени изменение значения одного признака сопровождается изменением значения другого признака в данной выборке.
Значения коэффициента корреляции изменяются в интервале от –1 до 1. Знак (плюс или минус) при коэффициенте корреляции указывает направление связи.
При отрицательном значении коэффициента корреляции связь обратная, т.е. чем больше значение одного признака, тем меньше значение второго признака. При положительном знаке связь прямая: чем больше, тем больше. Принята следующая классификация силы корреляции в зависимости от значения коэффициента корреляции r, взятого по модулю (без учета знака):
· от 0 до 0,2 – связь очень слабая;
· от 0,2 до 0,4 – связь слабая;
· от 0,4-0,6 – связь средняя;
· от 0,6 до 0,8 – связь сильная;
|
|
|
· от 0,8 до 1 – связь очень сильная.
Вместе с тем даже в случае сильной связи, она может быть статистически не значима, например, в случае малого объема выборки.
Значимость коэффициента можно оценить следующим образом:
Для случая, когда объем совокупности меньше 50, рассчитывается t-критерий по формуле:
 .
.
Для случая, когда объем совокупности больше 50, рассчитывается Z-критерий по формуле:
 .
.
В большинстве случаев востребованным и весьма полезным может оказаться построение и анализ диаграмм рассеяния. Диаграмма рассеяния (точечная диаграмма) – математическая диаграмма, изображающая значения двух переменных в виде точек на декартовой плоскости. На такой диаграмме производится визуальный анализ объектов исследования с учетом по форме связи («облака» точек) и по наличию выбросов на диаграмме рассеяния. «Выбросы» – крайние значения признаков, не характерные для данной выборки, слишком большие или слишком малые значении, аномальные, при удалении которых связь полностью может измениться.
Варианты скоплений точек показаны на рис. 25.
Так, на рис. а пример абсолютной отрицательной корреляции, на рис. б – сильной положительной корреляции. На рис. в – взаимосвязь между значениями не усматривается, на рис. г взаимосвязь наличествует, но это не линейная зависимость, а параболическая.

Рис. 25. Варианты скоплений точек на диаграммах рассеяния
Наличие корреляции не является доказательством причинно-следственной связи признаков. Наличие корреляции свидетельствует о том, что, либо одно явление является частичной причиной другого, либо оба явления – следствие общих причин. Для выводов о причинно-следственной связи необходимо использовать знание социологической теории.
Отношение «причина – следствие» возможно на основании логического продолжения корреляционного анализа – регрессионного. Продолжать следует в том случае, когда найдено логическое объяснение полученной связи и можно утверждать, который из коррелированных между собой показателей причина, а который – следствие.
Регрессионный анализ устанавливает формы зависимости между случайной величиной У (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость обычно определяется некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров. В ходе регрессионного анализа на основании выборочных данных находят оценки этих параметров, определяются статистические ошибки оценок или границы доверительных интервалов и проверяется соответствие (адекватность) принятой математической модели экспериментальным данным.
Регрессионный анализ всегда проводится после корреляционного анализа, когда между переменными установлена взаимосвязь. Регрессионный анализ используется для прогнозирования одной переменной на основании другой (как правило, Y на основании X), или показывает, как можно управлять одной переменной с помощью другой.
Моделью является уравнение регрессии. В случае определения формы взаимосвязи двух признаков в регрессионном анализе изменение зависимой переменной Y зависит от изменения независимой переменной Х. При этом вопрос, какую именно переменную считать за Х, а какую принимать за Y – решает исследователь, исходя из логики изучаемого процесса. В этом принципиальное отличие корреляционного и регрессионного анализов. Важность регрессионного анализа в том, что на основе регрессионных моделей разрабатываются прогнозы развития зависимой переменной Y от изменений независимой (нескольких независимых) переменной Х. Если модель построена на основании нескольких переменных Х, то регрессия называется множественной.
Определение формы зависимости между переменными X и Y является одной из главных задач регрессионного анализа. Для этого необходимо построить уравнение регрессионной связи между Y и X (уравнение регрессии) следующего вида:
Y = f (x) + e,
в котором f (x) называется функцией регрессии, а e – величина, учитывающая случайные воздействия. Для выборочных данных уравнение регрессионной связи удобно представить следующим образом:

При наличии случайной составляющей e i значения yi имеют определенный разброс. Поэтому нет смысла подбирать функцию регрессии, проходящую через все точки. Основное правило подбора вида функции регрессии заключается в том, чтобы все точки диаграммы рассеяния были сконцентрированы около графика этой функции.
На практике, поскольку мы располагаем выборочными данными, невозможно точно построить функцию регрессии, можно только получить ее оценку, которую обозначим как  . Уравнение, включающее оценку для функции регрессии, называется выборочным уравнением регрессии и имеет вид:
. Уравнение, включающее оценку для функции регрессии, называется выборочным уравнением регрессии и имеет вид:  . Построив «выборочную» функцию регрессии далее необходимо проверить достоверность функции и ее параметров, а также провести оценку неизвестных значений (прогноз) зависимой переменной Y.
. Построив «выборочную» функцию регрессии далее необходимо проверить достоверность функции и ее параметров, а также провести оценку неизвестных значений (прогноз) зависимой переменной Y.
Простейшей, с точки зрения анализа, является линейная взаимосвязь между X и Y, которая выражается в том, что точки на диаграмме рассеяния случайным образом группируются вдоль прямой линии, имеющей наклон (вверх или вниз). Регрессионная линейная модель задается уравнением Y= a + b *X, при этом переменная Y выражается через константу (a) и коэффициент (b), умноженный на переменную X. Константу называют также свободным членом а, а угловой коэффициент – регрессионным или b -коэффициентом. В уравнении регрессии оба коэффициенты должны быть значимы, как и вся модель.
В случае рассмотрения зависимости между одной зависимой переменной У и несколькими независимыми Х1, X2,..., Хn, говорят о множественной регрессии. В этом случае регрессионное линейное уравнение имеет вид:
У = а + b1Х1 + b2Х2 +... + bnХn,
где b1, b2,..., bn – требующие определения коэффициенты при независимых переменных Х1, Х2,..., Хn;
а – свободный член (константа).
Линия регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимым переменным (X). Однако, природа редко (если вообще когда-нибудь) бывает полностью предсказуемой и обычно имеется существенный разброс наблюдаемых точек относительно подогнанной прямой. Отклонение отдельной точки от линии регрессии (от предсказанного значения) называется остатком.
Мерой эффективности регрессионной модели является коэффициент детерминации R2 (R-квадрат). Коэффициент детерминации (R-квадрат) определяет, с какой степенью точности полученное регрессионное уравнение описывает (аппроксимирует) исходные данные.
Исследуется также значимость регрессионной модели с помощью F-критерия (Фишера). Если величина F-критерия значима (р < 0,05), то регрессионная модель является значимой.
Достоверность отличия коэффициентов b1, b2, b3..., bn от нуля проверяется с помощью критерия Стьюдента. В случаях, когда р > 0,05, коэффициент может считаться нулевым, а это означает, что влияние соответствующей независимой переменной на зависимую переменную недостоверно, и эта независимая переменная может быть исключена из уравнения.
В Microsoft Excel и OpenOffice.org Calc используются три метода корреляционно-регрессионного анализа: инструменты анализа Корреляция и Регрессия и соответствующие статистические функции, графический с использованием команды Добавить линию тренда.
2. Использование Microsoft Excel и OpenOffice.org Calc
при анализе взаимосвязи количественных признаков
2.1. Использование инструмента Анализ данных в Microsoft Excel
Рассмотрим возможности использования пакета Анализ данных в Microsoft Excel при проведении корреляционно-регрессионного анализа.
Необходимо проанализировать статистические данные по странам Восточной Европы (рис. 26).
Для проведения корреляционного анализа нужно в меню Сервис выбрать опцию Анализ данных. В появившемся окне выбрать опцию. Корреляция.
В окне «Корреляция» введите Входной интервал – те данные, которые подлежат анализу. Группирование в нашем примере осуществляется по столбцам (столбцы содержат отдельные показатели по странам). Поле Метки в первой строке следует отметить в том случае, если входной интервал задан вместе с заголовками столбцов/строк.
В разделе окна Параметры вывода укажите, куда следует выводить корреляционную матрицу (квадратная (или прямоугольная) таблица, в которой на пересечении соответствующих строки и столбца находится коэффициент корреляции между соответствующими параметрами).

Рис. 26. Окно «Корреляция»
В нашем примере результат выведется на отдельной странице (рис. 27)
Прокомментируем полученную матрицу. Как видно из полученных результатов наибольшая корреляционная зависимость (очень сильная) наблюдается между показателями «Доля замужних женщин 15-49 лет, использующих все виды контрацептивов (%)» и «Доля замужних женщин 15-49 лет, использующих современные контрацептивы (%)», где r=0,921214 – скорее всего эти факторы являются следствием одной общей причины. Наименьшая (очень слабая) между «Доля замужних женщин 15-49 лет, использующих все виды контрацептивов (%)» и «Коэффициент рождаемости (на 1000 жителей)», где r=-0,0193514. В то время как взаимосвязь признаков «Доля городского населения, %» и «Число мобильных телефонов на 100 жителей» можно оценить как сильную, т.к. r=0,66587291, при этом, скорее всего второй признак является следствием первого, но, скорее всего, на «Число мобильных телефонов на 100 жителей» оказывают влияние еще какие-то факторы.

Рис. 27. Корреляционная матрица
Для демонстрации возможностей графического метода построим точечную диаграмму (диаграмму рассеяния) по этим признакам (рис. 28).

Рис. 28. Построение диаграммы рассеяния (точечной диаграммы)
Полученную диаграмму дополним линией регрессии и коэффициентом достоверность аппроксимации, щелкнув правой кнопкой мыши по точкам диаграммы и выбрав в контекстном меню пункт Линия тренда (рис. 29, 30).

Рис. 29. Добавление линии тренда

Рис. 30. Добавление параметров линии тренда
Полученная точечная диаграмма позволяет судить не только о разбросе точек вокруг предполагаемой линии тренда, но и увидеть аномальные совместные проявления признаков (рис. 31). Так, выделенная точка построена по значениям показателей «Доля городского населения, %» и «Число мобильных телефонов на 100 жителей» Белоруссии. Анализ и интерпретация появления аномалий должны производиться исходя из знаний о социально-экономической природе рассматриваемого объекта.


Рис. 31 Точечная диаграмма
Для реализации процедуры Регрессия необходимо: выбрать в меню Сервис команду Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия.
В появившемся диалоговом окне (рис. 32) задать:
Входной интервал Y – диапазон (столбец), содержащий данные со значениями объясняемой переменной;
Входной интервал Х – диапазон (столбцы), содержащий данные с заголовками.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении (а);
Уровень надежности – уровень значимости, (например, 0,05);
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист – поставить значок и задать имя нового листа (Отчет – регрессия), в котором будет сохранен отчет.
Если необходимо получить значения и график остатков, а также график подбора (чтобы визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели), установите соответствующие флажки в диалоговом окне.

Рис. 32. Окно «Регрессия»
Рассмотрим результаты регрессионного анализа (рис. 33, 34).
Множественный R – коэффициент корреляции
R-квадрат – это коэффициент линейной детерминации. Коэффициент является одной из наиболее эффективных оценок адекватности регрессионной R2 модели, мерой качества уравнения регрессии в целом (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям.
Если R-квадрат > 0,95, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат < 0,6, принято считать, что точность аппроксимации недостаточна и модель требует улучшения (введения новых независимых переменных, учета нелинейностей и т. Д.).
Нормированный R-квадрат – скорректированный (адаптированный, поправленный) коэффициент детерминации.
Недостатком коэффициента детерминации R-квадрат является то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать нормированный, который в отличие от R-квадрат может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
Наблюдения – число наблюдений (в нашем случае 10 стран).
Df – число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант.
F и Значимость F позволяют проверить значимость уравнения регрессии, т.е. установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
SS – Сумма квадратов отклонений значений признака Y.
MS – Дисперсия на одну степень свободы.
F – Наблюдаемое (эмпирическое) значение статистики F, по которой проверяется гипотеза равенства нулю одновременно всех коэффициентов модели. Значимость F – теоретическая вероятность того, что при гипотезе равенства нулю одновременно всех коэффициентов модели F -статистика больше эмпирического значения F.
На уровне значимости α=0,05 гипотеза H0: b1 =0отвергается, если Значимость F<0.05, и принимается, если Значимость F ≥ 0.05. В нашем примере Значимость F >0.05, что говорит о неадекватности модели Следует понимать, что «плохой результат – тоже результат» – полученная оценка модели важна для ее последующего осмысления, т.к. дальнейший анализ может подсказать какие из независимых переменных незначимы и ухудшают качество модели.
Значения коэффициентов регрессии находятся в столбце Коэффициенты и соответствуют:
– У-пересечение – a;
– переменная XI – b1;
– переменная Х2 – b2 и т. Д.
Таким образом, получена следующая модель регрессии:
Y=1.2247X1+0.00108X2+19.9776
t -статистика соответствующего коэффициента.
P-Значение – вероятность, позволяющая определить значимость коэффициента регрессии. В случаях, когда Р-Значение > 0,05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.
В нашем случае оба коэффициента оказались «нулевыми», а значит обе независимые переменные не влияют на модель.
Нижние 95% – Верхние 95% – доверительный интервал для параметра, т.е. с надежностью 0.95 этот коэффициент лежит в данном интервале. Поскольку коэффициент регрессии в исследованиях имеют четкую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов. Так, например, «Доля городского населения, в %» не может лежать в интервале -0,25 ≥ b1 ≥ 2,7. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.

Рис. 33. Вывод итогов регрессионного анализа
Предсказанное Y - теоретические (расчетные) значения результативного признака.
Остатки – остатки по модели регрессии.

Рис. 34. Вывод остатков и вероятности по результатам регрессионного анализа
На основе данных об остатках модели регрессии был построен график остатков (рис. 35, 36) и график подбора – поле корреляции фактических и теоретических (расчетных) значений результативной переменной (рис. 37, 38).



|

Рис. 35. График остатков по значениям признака «Доля городского населения, %»

Рис. 36. График остатков по значениям признака
«Число мобильных телефонов на 100 жителей»


|

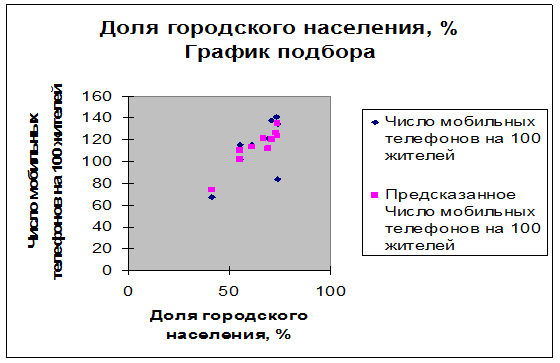
Рис. 37. График подбора для признаков «Доля городского населения, %»
и «Число мобильных телефонов на 100 жителей»

Рис. 38. График подбора для признаков «Доля городского населения, %»
и «Число мобильных телефонов на 100 жителей»
Рассмотрение графиков подбора позволяет предположить, что качество модели можно усовершенствовать, если исключить из нее «ВВП на душу населения с учетом паритета покупательной способности в 2008 г., (US$)» как «плохо» предсказуемое, и, возможно, исключив данные по Белоруссии как аномальные значения.
Попробуйте произвести соответствующие изменения в модели и проанализировать самостоятельно.
2.2. Использование специальных функций
Для анализа зависимостей можно использовать и специальные функции (табл. 12). Обратите внимание, что некоторые из приведенных функций – функции работы с массивами.
Таблица 12
| Функция Excel (рус.) | Функция Calc (англ.) | Назначение |
| КОРРЕЛ | CORREL | Возвращает коэффициент корреляции |
| ЛИНЕЙН | LINEST | Возвращает массив коэффициентов линейного уравнения регрессии |
| ТЕНДЕНЦИЯ | TREND | Возвращает значения в соответствии с линейным уравнением регрессии (используется для получения предсказанных значений У в требуемых точках) |
| ЛГРФПРИБЛ | LOGEST | Возвращает коэффициенты экспоненциального уравнения регрессии |
| FPACПOБP | FINV | Возвращает обратное значение для F-распределении вероятностей |
3. Задания для самостоятельной работы
Задание 1
Оцените взаимосвязь признаков таблицы 23.
Задание 2
Определите, к каким данным таблицы 20 возможно применить корреляционно-регрессионный анализ. Произведите соответствующий анализ.
Задание 3
Оцените взаимосвязь признаков таблицы 13.
Таблица 13[3]
Демографические показатели некоторых промышленно
развитых стран мира (2011г.)
| Страна | Общий коэффициент разводимости (на 1000 жителей) | Средний возраст женщин при вступления в первый брак | |
| Австрия | 2,10 | 33,6 | |
| Бельгия | 3,00 | 28,8 | |
| Болгария | 1,50 | 26,8 | |
| Босния и Герцеговина | 0,40 | 25,6 | |
| Венгрия | 2,40 | 28,6 | |
| Германия | 2,30 | 30,2 | |
| Дания | 2,60 | 32,1 | |
| Испания | 2,20 | 31,0 | |
| Латвия | 2,20 | 26,8 | |
| Литва | 3,00 | 26,3 | |
| Македония | 0,80 | 25,1 | |
| Норвегия | 2,10 | 31,0 | |
| Польша | 1,60 | ||
|
|
|


