3. Порядок вычисления итоговых величин однофакторного дисперсионного анализа

3. Порядок вычисления итоговых величин однофакторного дисперсионного анализа

 

Порядок вычисления итоговых величин однофакторного дисперсионного анализа рассмотрим на примере анализа однофакторного неравномерного (не ортогонального) комплекса. Принципиально, алгоритм расчетов неравномерных комплексов применим и для равномерных комплексов, но не наоборот.

 

1. Пусть требуется оценить влияние принадлежности к разным видам тополей, как аборигенным, так и интродуцированным в Нижегородскую область, на пигментный состав их листового аппарата в ситуации, когда их потомство размещено в границах одного опытного участка на территории

 

 

Применяемый математический аппарат

 

Математическим инструментом вычисления дисперсионного отношения Фишера и расчета величин доли влияния организованного фактора на общий фон фенотипической дисперсии выступает дисперсионный анализ. Особенностью любого, однофакторного в том числе, дисперсионного анализа является предоставляемая им возможность разложения общей дисперсии на дисперсию межклассовую (факториальную) и внутриклассовую (остаточную). Это и есть принципиальная схема однофакторного дисперсионного анализа. Напомним, что условиями анализа предусматривается построение дисперсионных комплексов, в каждом из которых содержится некоторое число классов (групп значений), объединяющих некоторое количество значений по принципу принадлежности каждого значения группы только к объектам этой группы и не принадлежность их к объектам любой другой группы (класса). В результате анализа определяют дисперсию признака, обусловленную различиями в классовой принадлежности объектов (различия между классами), и различия, обусловленные случайным варьированием, не вызываемым действием различий между классами (внутриклассовую или остаточную дисперсию). Распределение признаков объектов по классам осуществляется на основе устанавливаемых границ градаций действующего фактора, собственно вызывающего образование различий. Это следует понимать так, что действие какого-либо анализируемого фактора (время, расстояние, наследственная специфика и др. ) приводит к разделению объектов на некоторые группы, отличные друг от друга. В пределах каждой из групп объектов не существует различий, вызываемых действием учитываемого фактора. Тогда имеющаяся неоднородность объектов в пределах какой-либо группы может быть объяснена только случайным варьированием.

 

Относя все вышесказанное к селекционным проблемам, можно принять следующую прикладную (для решения задач селекционной оценки древесных видов и их популяций) схему дисперсионного анализа.

 

 

Схема дисперсионного анализа и условия расчета

 

1. Древесные растения и кустарники (оценку ведем в пределах одного вида) размещенные на некоторой (в той или иной степени определенной границами) территории будем рассматривать как популяцию. Происхождение каждого из учитываемых растений семенное, и, следовательно, они различаются, в том числе и генотипически. Принимаем (условно) то обстоятельство, что фенотипические различия между особями будут обусловлены влиянием генотипических различий (влияние аддитивной и неаддитивной составляющих генотипической дисперсии) и влиянием различий в условиях среды (влияние случайной или средовой дисперсии).

 

2. Различия значений метамерных (повторяющихся) признаков (значения параметров шишек, плодов, семян, листьев, почек, углов крепления ветвей к стволу и т. п. ) в пределах одного растения будут обусловлены только ненаследственными причинами (различиями в условиях освещенности, газообмена, питания и пр. ). Это следует из того обстоятельства, что все образовавшиеся метамерные части и органы растения сформировались под влиянием одного генотипа. Исключение могут составлять семена, образовавшиеся в результате опыления женских генеративных органов одного растения пыльцой различных деревьев. Принципиально такая возможность не исключена. Уровень изменчивости метамерных признаков принимается как уровень изменчивости, обусловленной факторами среды.

 

3. Тогда возникают предпосылки для оценки каждой из долей общей фенотипической изменчивости.

 

4. Для таксационных показателей, таких как высота дерева, диаметр ствола, объем ствола, параметры кроны, имеющих однозначное значение для каждого дерева, указанная схема дисперсионного анализа непригодна. Для таких признаков применение дисперсионного анализа должно предусматривать сравнение нескольких популяций между собой при наличии некоторого разнообразия в пределах популяций.

 

5. Остановимся на случае, когда анализу подвергаются метамерные признаки особей, образующих некоторую популяцию.

 

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАСЧЕТОВ

 

1. По имеющимся материалам (результаты натурных обследований природных популяций: получают у преподавателя) статистического учета одного из метамерных признаков заданного числа растений в популяции (обусловлено заданным уровнем точности и уровнем изменчивости признака в популяции: определяет преподаватель) осуществляют расчет основных статистик и определяют точность опытных данных. В случае достаточного уровня точности (не более 5%) приступают к собственно дисперсионному анализу по предлагаемому ниже алгоритму.

 

2. Исходные данные группируют в виде комбинационной таблицы таким образом, чтобы градации регулируемого (в нашем случае учитываемого) фактора (в нашем случае – это различия в генетической природе особей) располагались по горизонтали в верхней части таблицы. Обозначим действующий фактор через «А». Тогда в верхней горизонтальной строке таблицы окажутся порядковые номера учетных растений в популяции, соответствующие градациям действующего фактора (каждое растение – самостоятельная градация). Градации фактора «А» образуют столбцы, в которых располагаются варьирующие значения результативного признака (проявление в границах случайной изменчивости формирования признаков в пределах отдельной градации). Их называют вариантами или датами и обозначают «x_i». Они группируются по соответствующим градациям фактора А.

 

Исходная таблица значений признаков при организации

дисперсионного комплекса (пример составления)

 

Признак: (например, длина листовой пластинки, см или диаметр ствола, см и т. д. )

 

№ п/п	Номера учетных растений (действующий фактор А): а = 10
											Сумма
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
…..											…..

 

Примечание:

1. Исходные данные в таблицу 1 заносят из таблиц дидактического материала, которые выдаются каждому студенту преподавателем. Преподаватель определяет: один из анализируемых признаков в каждой из таблиц; количество учетных растений, привлекаемых для анализа; количество учтенных метамеров по каждому из учетных растений и т. д., т. п.

2. Количество столбцов определяется числом учетных растений, включенных в анализ, а количество строк – числом учтенных метамеров.

 

3. Принимаем основные алгоритмы вычислений в дисперсионном анализе.

 

3. 1. Общая сумма квадратов отклонений, которая в рабочих алгоритмах чаще используется в виде правой части равенства.

 

 

 

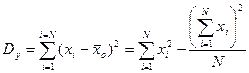
3. 2. Межгрупповая (факториальная) сумма квадратов отклонений.

 

3. 3. Внутригрупповую, или остаточную, сумму квадратов отклонений определяют по разности между общей и межгрупповой суммами квадратов отклонений.

 

 

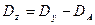
3. 4. Числа степеней свободы определяем по следующим формулам:

 

 

3. 5. Определяют средние квадраты отклонений или дисперсии: их находят через отношение соответствующих сумм квадратов отклонений к соответствующим степеням свободы.

 

 

3. 6. Определяют эффективность действия фактора А (в нашем случае эффективность действия фактора различий между особями) на результирующий признак (в нашем случае на конкретное проявление признака каждой особью). Для этого используют дисперсионное отношение или критерий Фишера F.

 

 

Так как дисперсионное отношение – величина случайная, его сравнивают с табличным (стандартным) значением.

 

3. 7. В предложенном алгоритме расчета дисперсионного отношения можно легко увидеть некоторое общее содержание конкретных формул (в расчете общего квадрата отклонений и в расчете факториального квадрата отклонений). Эту общую часть часто выражают знаком « Н » или иным символом.

 

 

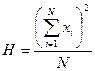
4. Если доказана достоверность влияния действующего фактора, то с помощью дисперсионного анализа можно определить и силу его влияния на результирующий признак. Силу влияния фактора определяют как долю факториальной или межгрупповой изменчивости в общем варьировании признака. Существует ряд способов расчета этого показателя. Наиболее распространенными являются способ Плохинского (1966, 1970) и способ Снедекора (1961).

 

4. 1. При реализации способа Плохинского исходят из того, что справедливо равенство D_y=D_x+D_z, которое осуществляется в любом дисперсионном комплексе. В этом способе расчета оперируют суммами квадратов отклонений. Делением всех членов этого равенства на D_y получают:

 

 

Показатель h² принимают как силу влияния действующего фактора, и в ряде случаев его рассматривают как показатель степени наследственной обусловленности различий между особями в популяции или как коэффициент наследуемости в широком смысле. Это справедливо на том основании, что в рассматриваемом примере фактором, вызывающим различия между градациями дисперсионного комплекса, выступает именно разница в генотипах объектов, относимых к разным градациям.

                                                                                                                                       

Критерием достоверности этого показателя служит его отношение к своей ошибке, которая вычисляется по следующей приближенной формуле:

 

, где

 

- a – число градаций фактора А;

- N – общее число вариант: N = Σ n_i;

- n_i – число вариант в отдельной градации дисперсионного комплекса;

 

Нулевая гипотеза отвергается, если

 

 

Стандартное значение критерия Фишера берется по таблице. При этом учитывают заданный уровень значимости и число степеней свободы: k₁=a-1 (находится в верхней горизонтальной строке таблицы), k₂=N-a (находится в первом вертикальном столбце таблицы).

 

ЗАДАНИЕ к пункту 4. 1.

Выполните расчет значений коэффициента наследуемости в широком смысле по методу Плохинского, используя исходный материал, полученный у преподавателя.

 

4. 2. В способе Снедекора в качестве показателя силы влияния используют отношение дисперсий (средних квадратов отклонений), а именно межгрупповой дисперсии к общей дисперсии для всего комплекса, которая определяется как сумма дисперсий межгрупповой и остаточной:

 

.

 

При этом межгрупповая дисперсия определяется с учетом влияния на групповые характеристики комплекса случайных нерегулируемых факторов (исходя из тезиса: различия между особями обусловлены не только влиянием собственно различиями в их происхождении, но и различиями в условиях произрастания каждого из них). Расчет факториальной дисперсии в этом случае ведут по формуле:

 

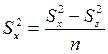, где

 

-  – факториальная дисперсия, без учета дисперсии, вызванной влиянием среды;

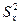- – межгрупповой средний квадрат отклонений или «неисправленная» межгрупповая дисперсия;

- – остаточная дисперсия;

- численность вариант в отдельных группах (градациях действующего фактора) дисперсионного комплекса при равенстве численностей внутри всех градаций.

 

Если числа вариант в градациях комплекса неодинаковы (неравномерный дисперсионный комплекс), то величина n определяется по формуле:

 

, где

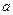- число градаций фактора А (в расчетах по нашему примеру – это число особей в выборке);   

- общее число наблюдений в дисперсионном комплексе;         

- число наблюдений в пределах каждой из градаций фактора А;

 

i = 1…a – порядковый номер градации.

 

Тогда показатель силы влияния фактора приобретает следующее выражение:

 

 

Достоверность показателя силы влияния фактора, определяемого по методу Снедекора, устанавливается обычным в дисперсионном анализе способом, т. е. посредством дисперсионного отношения (критерия Фишера)

 

 ,

 

величина которого сравнивается с критическим табличным значением для принятого уровня значимости и чисел степеней свободы k_x = а-1и k_z=N-a.

 

ЗАДАНИЕ к пункту 4. 2.

Выполните расчет значений коэффициента наследуемости в широком смысле по методу Снедекора, используя исходный материал, полученный у преподавателя.

 

ВНИМАНИЕ (Бессчетнов В. П. )

Вместе с тем, данный метод расчета имеет свои ограничения. В частности, в ситуации, когда величина случайной дисперсии велика на столько, что превышает значения факториальной дисперсии (  ≥ 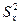), значения коэффициента наследуемости принимают отрицательное значение, а в случае их равенства принимают нулевое значение.

 

 гибридов тополей, получаемых для создания промышленных плантаций. Напомним, что тополя относятся к двудомным растениям, т. е. их особи являются разнополыми. Учитываемым признаком будет объем ствола к установленному возрасту (20 лет). Планом гибридизации было предусмотрено использование в качестве отцовских особей 3-х перспективных форм тополя белого (Populus alba L., ), а в качестве материнских – 8 особей тополя Болле (Populus bolleana Lauche). При этом схема скрещивания и количество оставшихся к моменту учета гибридов по каждой комбинации скрещивания будет отражена в таблице 1.

 

Таблица 1.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: