 |
Дубли и дополнительный материал
|
|
|
|
Дубли и дополнительный материал
Примечание: ***************
Одной из сфер применения двухфакторного иерархического анализа является определение общей комбинационной способности (ОКС) и специфической комбинационной способности (СКС) при осуществлении селекции методом гибридизации. В этих ситуациях оценивается степень проявления (сохранения) признаков родителей у потомства первого поколения (F1). Иерархические комплексы строятся по следующей схеме: иерархическим уровнем высшего порядка (фактор А) выступает набор комбинаций скрещивания (диалельных прямых и реципрокных), рангом низшего порядка (фактор В) является набор повторностей каждой комбинации скрещивания (в идеальном случае на нескольких клонах материнской особи при одном источнике пыльцы) в пределах одной комбинации скрещивания.
Примечание:
В учебнике М. М. Котова (стр. 134-135) приведена некорректная схема двухфакторного комплекса: не указывается, что именно является повторностями испытания гибридного потомства. Вместе с тем известно (Лакин, 1989; Меркурьева, 19** и др. ), что результаты дисперсионного анализа (особенно многофакторного) в значительной степени зависят от характера конкретного распределения (конкретной комбинации) действующих факторов по их градациям. В случае, если повторности испытания искусственно выделены в пределах какой либо комбинации скрещивания - скрещивание проведено в пределах одной пары деревьев – они (повторности) по своей сути будут представлять одну и ту же совокупность и будут являться одной и той же выборкой. В такой ситуации распределение всего количества гибридов данной комбинации на повторности испытания гибридного потомства будет абсолютно искусственным и не значимым, что в свою очередь может исказить результаты дисперсионного анализа.
|
|
|
ВНИМАНИЕ!
Здесь (по Котову) уместнее в качестве высшего уровня иерархии (фактор А) рассматривать отцовские особи (особи, выступающие отцовскими) в комбинациях скрещивания (когда растения выступают источником пыльцы), а в соподчиненном уровне иерархии факторов (фактор В) рассматривать комбинации скрещивания каждого отцовского дерева с различными материнскими (выступающими в качестве материнских) особями. То есть комбинации скрещивания каждого отцовского дерева будут являться градациями фактора низшей иерархии в пределах каждого отцовского дерева, выступающего фактором высшей иерархии.
Диалельное скрещивание – это скрещивание испытываемых деревьев (и кустарников) во всех возможных комбинациях. Оно может быть прямым (только прямым) и реципрокным (прямым и обратным).
При прямом скрещивании число возможных комбинаций скрещивания равно:
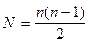 . где
. где
n – число растений участвующих в гибридизации, при условии, что все они однодомны.
При реципрокном (прямом и обратном) скрещивании число возможных комбинаций равно:
 .
.
ПРИМЕР.
Требуется оценить общую и специфическую комбнационную способность родительских деревьев дуба черешчатого по высоте 20-летнего потомства, полученного от прямых диаллельных скрещиваний. Исходные данные приведены в таблице (*******).
Расчет ведется по схеме равномерного (ортогонального) дисперсионного двухфакторного комплекса.
Таблица ***.
Высота гибридов дуба (в возрасте 20 лет)
| № варианта | Комбинация скрещивания | Повторности | Высота, м | |||||||||||
| 1х2 | 5, 5 | 5, 4 | 6, 0 | 6, 2 | 6, 1 | 6, 4 | 6, 1 | 6, 0 | 5, 9 | 6, 0 | ||||
| 5, 9 | 6, 1 | 6, 1 | 6, 3 | 5, 8 | 5, 7 | 5, 1 | 6, 4 | 6, 0 | 6, 1 | |||||
| 6, 4 | 6, 0 | 6, 2 | 5, 8 | 5, 9 | 5, 7 | 5, 0 | 6, 0 | 6, 2 | 6, 3 | |||||
| 1х3
| 6, 5 | 6, 5 | 6, 1 | 5, 5 | 5, 4 | 4, 9 | 6, 1 | 6, 3 | 6, 4 | 6, 3 | ||||
| 6, 0 | 5, 9 | 5, 8 | 6, 3 | 6, 5 | 5, 2 | 6, 3 | 6, 2 | 6, 1 | 6, 1 | |||||
| 6, 3 | 6, 1 | 5, 4 | 5, 0 | 6, 5 | 6, 3 | 6, 0 | 5, 9 | 5, 8 | 5, 6 | |||||
| 1х4 | 3, 0 | 3, 4 | 2, 8 | 3, 2 | 3, 0 | 3, 0 | 2, 9 | 2, 8 | 3, 6 | 3, 4 | ||||
| 3, 5 | 3, 4 | 3, 4 | 3, 2 | 2, 8 | 2, 8 | 2, 0 | 4, 1 | 4, 1 | 2, 1 | |||||
| 4, 0 | 4, 1 | 3, 2 | 3, 1 | 2, 5 | 2, 5 | 3, 8 | 2, 1 | 3, 0 | 3, 1 | |||||
| 2х3 | 3, 1 | 3, 0 | 2, 8 | 2, 6 | 3, 4 | 3, 0 | 2, 5 | 2, 1 | 2, 9 | 3, 1 | ||||
| 4, 1 | 3, 0 | 3, 6 | 3, 4 | 2, 8 | 2, 8 | 2, 9 | 3, 1 | 3, 2 | 3, 4 | |||||
| 3, 9 | 3, 9 | 3, 6 | 3, 5 | 3, 5 | 2, 5 | 3, 4 | 3, 8 | 4, 0 | 4, 0 | |||||
| 2х4 | 2, 5 | 4, 1 | 4, 1 | 3, 9 | 3, 5 | 3, 5 | 3, 9 | 4, 0 | 4, 9 | 2, 6 | ||||
| 4, 1 | 2, 6 | 4, 1 | 3, 9 | 3, 6 | 3, 8 | 3, 8 | 4, 1 | 3, 6 | 3, 8 | |||||
| 4, 0 | 4, 1 | 4, 1 | 4, 0 | 4, 9 | 3, 9 | 3, 9 | 3, 8 | 3, 5 | 3, 5 | |||||
| 3х4 | 3, 5 | 3, 5 | 3, 8 | 3, 5 | 2, 8 | 4, 1 | 4, 1 | 4, 0 | 2, 9 | 3, 9 | ||||
| 4, 1 | 4, 0 | 4, 0 | 4, 1 | 4, 0 | 3, 9 | 3, 9 | 3, 2 | 3, 1 | 2, 9 | |||||
| 2, 8 | 2, 9 | 4, 9 | 4, 1 | 4, 0 | 3, 8 | 3, 8 | 3, 8 | 3, 4 | 3, 0 | |||||
**********8888
Принципиально возможно добавить информацию о дисперсионном анализе – базовая модель, многофакторная модель, иерархическая модель.
Таблица ***
Дисперсионный анализ высоты 20-летних гибридов дуба
|
Кри-те-рии |
Варианты опыта - Гибридные комбинации (а) а=6 Фактор высшей иерархии |
Сум-ма | |||||||||||||||||
|
а1 (1х2) |
а2 (1х3) |
а3 (1х4) |
а4 (2х3) |
а5 (2х4) |
а6 (3х4) | ||||||||||||||
|
Повторности испытания потомства (r=18) Фактор низшей иерархии | |||||||||||||||||||
| Hi | 5, 5 | 5, 9 | 6, 4 | 6, 5 | 6, 0 | 6, 3 | 3, 0 | 3, 5 | 4, 0 | 3, 1 | 4, 1 | 3, 9 | 2, 5 | 4, 1 | 4, 0 | 3, 5 | 4, 1 | 2, 8 |
|
| 5, 4 | 6, 1 | 6, 0 | 6, 5 | 5, 9 | 6, 1 | 3, 4 | 3, 4 | 4, 1 | 3, 0 | 3, 0 | 3, 9 | 4, 1 | 2, 6 | 4, 1 | 3, 5 | 4, 0 | 2, 9 | ||
| 6, 0 | 6, 1 | 6, 2 | 6, 1 | 5, 8 | 5, 4 | 2, 8 | 3, 4 | 3, 2 | 2, 8 | 3, 6 | 3, 6 | 4, 1 | 4, 1 | 4, 1 | 3, 8 | 4, 0 | 4, 9 | ||
| 6, 2 | 6, 3 | 5, 8 | 5, 5 | 6, 3 | 5, 0 | 3, 2 | 3, 2 | 3, 1 | 2, 6 | 3, 4 | 3, 5 | 3, 9 | 3, 9 | 4, 0 | 3, 5 | 4, 1 | 4, 1 | ||
| 6, 1 | 5, 8 | 5, 9 | 5, 4 | 6, 5 | 6, 5 | 3, 0 | 2, 8 | 2, 5 | 3, 4 | 2, 8 | 3, 5 | 3, 5 | 3, 6 | 4, 9 | 2, 8 | 4, 0 | 4, 0 | ||
| 6, 4 | 5, 7 | 5, 7 | 4, 9 | 5, 2 | 6, 3 | 3, 0 | 2, 8 | 2, 5 | 3, 0 | 2, 8 | 2, 5 | 3, 5 | 3, 8 | 3, 9 | 4, 1 | 3, 9 | 3, 8 | ||
| 6, 1 | 5, 1 | 5, 0 | 6, 1 | 6, 3 | 6, 0 | 2, 9 | 2, 0 | 3, 8 | 2, 5 | 2, 9 | 3, 4 | 3, 9 | 3, 8 | 3, 9 | 4, 1 | 3, 9 | 3, 8 | ||
| 6, 0 | 6, 4 | 6, 0 | 6, 3 | 6, 2 | 5, 9 | 2, 8 | 4, 1 | 2, 1 | 2, 1 | 3, 1 | 3, 8 | 4, 0 | 4, 1 | 3, 8 | 4, 0 | 3, 2 | 3, 8 | ||
| 5, 9 | 6, 0 | 6, 2 | 6, 4 | 6, 1 | 5, 8 | 3, 6 | 4, 1 | 3, 0 | 2, 9 | 3, 2 | 4, 0 | 4, 9 | 3, 6 | 3, 5 | 2, 9 | 3, 1 | 3, 4 | ||
| 6, 0 | 6, 1 | 6, 3 | 6, 3 | 6, 1 | 5, 6 | 3, 4 | 2, 1 | 3, 1 | 3, 1 | 3, 4 | 4, 0 | 2, 6 | 3, 8 | 3, 5 | 3, 9 | 2, 9 | 3, 0 | ||

| N=180 | ||||||||||||||||||
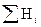
| 59, 6 | 59, 5 | 59, 5 | 60, 0 | 60, 4 | 59, 0 | 36, 1 | 37, 2 | 36, 5 | Σ Σ Hi= 774, 6 | |||||||||
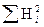
| 356, 04 | 355, 23 | 355, 47 | 362, 48 | 365, 98 | 348, 81 | 132, 27 | 140, 30 | 136, 95 | Σ Σ H2i=3615, 81 | |||||||||
| (Σ Н)2 ni | 355, 22 | 354, 02 | 354, 02 | 360, 00 | 364, 82 | 348, 10 | 130, 32 | 138, 38 | 133, 22 | (Σ Hi)2 Σ -------- ni 3595, 60 | |||||||||
| Σ Нi ni | 5, 96 | 5, 95 | 5, 95 | 6, 00 | 6, 04 | 5, 90 | 3, 61 | 3, 72 | 3, 65 | Σ Hi Σ -------- ni = 77, 51 | |||||||||
|
|
|
Решение задачи состоит из трех этапов:
1. доказательство существенности различий между гибридными комбинациями;
2. доказательство наличия эффектов комбинационной способности;
3. анализа комбинационной способности отдельных родителей и вариантов скрещивания.
1 этап.
Различия между гибридными комбинациями оцениваются по F критерию Фишера в двухфакторном дисперсионном комплексе (табл. ***).
1. Вычисляем общую сумму квадратов отклонений:

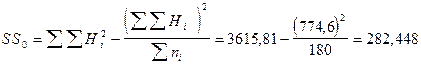 .
. 
2. На следующем этапе находим межгрупповой квадрат отклонений – общий факториальный квадрат отклонений:


Здесь величина
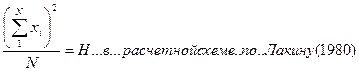
3. Далее находим вспомогательную промежуточную величину – сумму взвешенных квадратов сумм по фактору А (по отношению к числу вариант в пределах каждой соответствующей градации фактора А) для расчета суммы квадратов отклонений по фактору А:


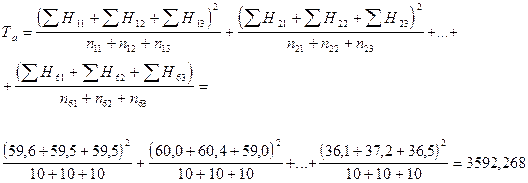
4. После этого определяем сумму квадратов отклонений по первому фактору – фактору высшего уровня иерархии (фактору А):

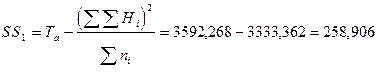
5. Рассчитываем остаточную сумму квадратов отклонений (по неорганизованным факторам):

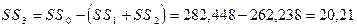
6. На следующем этапе вычисляем вариансы или средние квадраты отклонений: вариансу по первому фактору – фактору высшего уровня иерархии (А) – ms1 и остаточную вариансу – по неорганизованным факторам (Z) – ms3:
|
|
|
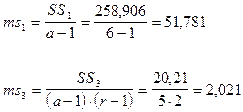
7. В заключении находим критерий Фишера:

Сравнение фактического значения критерия Фишера с его табличным значением (на трех уровнях значимости) показывает наличие существенных различий между гибридными комбинациями.
2 этап.
1. Вычисляются средние высоты гибридов по вариантам скрещивания, включая все повторности. Результаты заносятся в диаллельную таблицу. (табл. ****).
ВНИМАНИЕ!
В учебнике М. М. Котова (1997) не объясняется порядок заполнения таблицы!
При этом заполнение таблицы осуществляется так, что нижняя треугольная часть таблицы является соответствующим повторением её верхней треугольной части. В этом случае принимается во внимание тот факт, что обратных скрещиваний и самоопыления не проводилось. Тогда (! ) в нижней треугольной части (! ) будем иметь значения признака гибридного потомства, у которого номер материнского дерева является номером отцовского дерева, а номер отцовского – соответственно номером материнского.
Здесь уместнее было бы указать не номера отцовских и материнских деревьев, а «номера особей в прямых диаллельных скрещиваниях». Тогда становится понятным, что нижняя треугольная часть является соответствующим повторением (поскольку повторяются те же комбинации прямых скрещиваний) верхней треугольной части таблицы.
Таблица ****
| Номера отцовских деревьев | Номера материнских деревьев |
| |||
| - | 5, 95 | 5, 98 | 3, 15 | 15, 08 | |
| 5, 95 | - | 3, 24 | 3, 84 | 13, 03 | |
| 5, 98 | 3, 24 | - | 3, 66 | 12, 88 | |
| 3, 15 | 3, 84 | 3, 66 | - | 10, 65 | |
2. Находим общую полусумму средних значений высот деревьев – сумму одной из частей (верхней или нижней) полученной равномерной прямоугольной матрицы (только верхняя треугольная часть или только нижняя треугольная часть), т. е. суму значений признака (в нашем случае высоты деревьев) у особей, являющихся гибридным потомством при прямых диалльльных скрещиваниях.
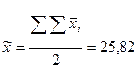
3. Подсчитываем суммы квадратов, обусловленные общей и специфической комбинационной способностью (SSg, SSs).
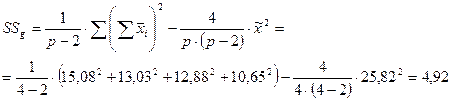
|
|
|
4. Подсчитываем суммы квадратов, обусловленные специфической комбинационной способностью (SSs):

где:
р – число родительских пар.
5. Проводим дисперсионный анализ комбинационной способности (табл. ****):
Таблица ****
Дисперсионный анализ комбинационной способности
родительских деревьев дуба
| № | Источники варьирования | Сумма квадратов отклонений SS | Число степеней свободы df | Средний квадрат отклонений ms | Критерий Фишера опытный Fфактич. |
| 1. | Общая комбинационная способность | SSg=4, 92 | df = p-1 = 3 | 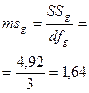
| 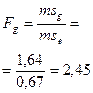
|
| 2. | Специфическая комбинационная способность | 
| 
| 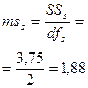
| 
|
| 3. | Случайные отклонения | 
| 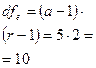 
| 
|  -
-
|
| Стандартные значения F | Fg = 3, 8 – 7, 0 – 13, 1 Fs = 4, 1 – 7, 9 – 14, 9 | ||||
Различия по общей и специфической комбинационной способности оказались недостоверными.
Если бы Fg был достоверен, можно было бы приступить к третьему этапу анализа.
3 этап.
Рассчитывается средний эффект (u) и эффекты общей комбинационной способности отдельных родителей (gi).
1. Рассчитываем средний эффект:

ВНИМАНИЕ!
Здесь уместнее объяснить, что средний эффект по сути является общим средним значением селектируемого (анализируемого) признака, отклонение от которого частного среднего значения признака гибридного потомства отдельного дерева во всех комбинациях его скрещивания со всеми остальными особями есть мера оценки ОКС.
Тогда предложенный алгоритм расчета общего среднего уместнее представить в более развернутой форме:
 , где
, где
 .
.
2. Рассчитываем эффекты общей комбинационной способности отдельных родителей:
ВНИМАНИЕ!
Возможно приведен не точный алгоритм расчета.

ВЫВОД.
Лучшей комбинационной способностью обладает первое дерево.
Сходный вывод напрашивается даже при общем знакомстве с исходными данными. В двух комбинациях из трех средняя высота гибридного потомства этого дерева почти в два раза превосходит высоту гибридных растений в других вариантах скрещивания.
ВНИМАНИЕ!
Скорее всего, более корректным будет алгоритм расчета, в котором при вычислении «средних» значений «контрольных» деревьев и полусибсового потомства, происходящего от одной особи и разных опылителей, в знаменателе первого сомножителя должна стоять разность между числом родительских пар и «единицей», а не «двойкой».
В этом случае ОКС каждого из родителей рассчитывается как разность между общим средним значение признака всех гибридов прямого диаллельного скрещивания во всех его комбинациях (когда растение выступает и как отцовское, и как материнское) и средним значение признака гибридного потомства одного из испытываемых родителей во всех комбинациях скрещивания, где одним (любым – материнским или отцовским) из родителей было испытываемое дерево.
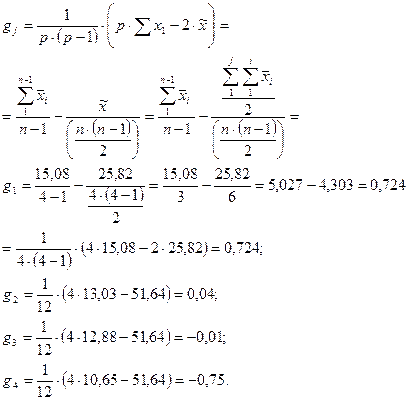
3. В случае достоверности mss далее вычисляются константы специфической комбинационной способности по формуле:

Для нашего примера получим:

4. Полученные значения констант (Sij) заносим в следующую таблицу (табл. *****):
Таблица ****
Эффекты общей (gi), константы специфической (Sij) и
вариансы специфической комбинационной способности (  )
)
| Номера отцовских деревьев | Константы СКС по номерам материнских деревьев, Sij | Эффекты ОКС, gi
| Вариансы СКС,
| |||
| - | 0, 50 | 0, 61 | -1, 10 | 1, 11 | 0, 56 | |
| 0, 50 | - | -1, 11 | 0, 61 | 0, 06 | 0, 60 | |
| 0, 61 | -1, 11 | - | 0, 51 | -0, 01 | 0, 60 | |
| -1, 11 | 0, 61 | 0, 51 | - | -1, 13 | 0, 59 | |
5. Вычисляются вариансы специфической комбинационной способности по каждому дереву:

6. Значения варианс СКС по каждому дереву заносим в ту же таблицу (табл. ***).
ВЫВОД.
По специфической комбинационной способности взятые для скрещивания деревья не отличаются друг от друга, на что и указывала раньше недостоверность mss.
|
|
|



