 |
Двухфакторный иерархический дисперсионный анализ
|
|
|
|
Двухфакторный иерархический дисперсионный анализ
| № |
Показа-тели |
Отцы |
Сумма | |||||||
|
А1 |
А2 |
А3 | ||||||||
|
Матери | ||||||||||
| В1 | В2 | В3 | В4 | В5 | В6 | В7 | В8 | |||
| 1. | Запас древеси-ны, м3 | 1, 0 0, 8 0, 6 0, 8 | 0, 9 0, 7 0, 8 0, 7 0, 5 | 1, 0 1, 1 0, 9 1, 0 | 1, 2 1, 0 1, 0 0, 9 1, 0 1, 1 0, 8 | 0, 9 0, 9 1, 0 0, 8 | 1, 1 1, 2 1, 0 0, 9 1, 0 0, 8 | 1, 0 1, 1 1, 1 0, 8 0, 9 | 0, 9 0, 9 0, 8 1, 1 0, 6 | a=3 b=8 |
| 2. | 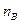
| Σ n=N | ||||||||
| 3. | 
| 3, 2 | 3, 6 | 4, 0 | 7, 0 | 3, 6 | 6, 0 | 4, 9 | 4, 3 | 36, 6 |
| 4. | 
| 10, 24 | 12, 96 | 16, 0 | 49, 0 | 12, 96 | 36, 0 | 24, 01 | 18, 49 | 1339, 56 |
| 5. | 
| 2, 56 | 2, 59 | 4, 0 | 7, 0 | 3, 28 | 6, 0 | 4, 80 | 3, 70 | 33, 93 |
| 6. | 
| 2, 64 | 2, 68 | 4, 02 | 7, 10 | 3, 26 | 6, 10 | 4, 87 | 3, 83 | 34, 50 |
| 7. | 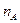
| |||||||||
| 8. | 
|
6, 8 |
14, 6 |
15, 2 | 36, 6 | |||||
| 9. | 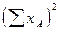
|
46, 24 |
213, 16 |
231, 04 | - | |||||
| 10. | 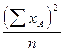
|
5, 14 |
14, 21 |
14, 44 | 33, 79 | |||||
2. Используя материалы первичных наблюдений, приведенные в таблице, вычисляем промежуточные вспомогательные величины.
2. 1. Средний квадрат суммы вариант:
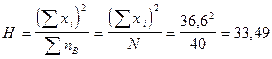 .
.
3. Затем находим суммы квадратов отклонений.
3. 1. Общая сумма квадратов отклонений:
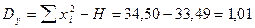 .
.
3. 2. Межгрупповая сумма квадратов отклонений:
 .
.
3. 3. Остаточная сумма квадратов отклонений:
 .
.
3. 4. Сумма квадратов отклонений по фактору А:
 .
.
3. 5. Сумма квадратов отклонений по фактору В:
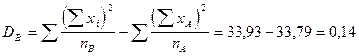 .
.
4. Определяем числа степеней свободы.
4. 1. Общее число степеней свободы (для общей дисперсии):
 .
.
4. 2. Число степеней свободы по фактору А (для дисперсии по фактору А ):
 .
.
4. 3. Число степеней свободы по фактору В (для дисперсии по фактору В ):
|
|
|
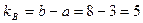 .
.
4. 4. Число степеней свободы по случайным факторам (для остаточной дисперсии, которую рассматривают как неорганизованный фактор и обозначают индексом Z ):
 .
.
5. Находим средние квадраты отклонений по факторам, используя полученные величины соответствующих сумм квадратов отклонений и числа степеней свободы.
5. 1. По фактору А – фактору высшего уровня иерархии:
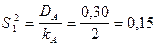
5. 2. По фактору В – фактору низшего уровня иерархии:

5. 3. По остаточной вариации – по случайным факторам – Z:

5. 4. Результат записываем в таблицу 2:
Таблица 2.
Результаты дисперсионного анализа гибридов тополей
|
Вариация | Степени свободы | Суммы квад-ратов | Средние квад-раты |
Дисперсионные отношения | ||
| Fфакт | Fст | |||||
| 5% | 1% | |||||
| По фактору А | 0, 30 | 0, 150 | FA = S21/S22 = 0, 150/0, 028 = 5, 4 | 3, 3 | 5, 3 | |
| По фактору В | 0, 14 | 0, 028 | FB = S22/S2Z = 0, 028/0, 018 = 1, 6 | 2, 7 | 3, 7 | |
| Остаточная | 0, 57 | 0, 018 | - | - | - | |
| Общая | 1, 01 | - | - | - | - | |
Статистически доказанным оказалось влияние фактора А.
6. Определяем усредненные значения степеней свободы для неравномерных комплексов, позволяющие учесть различия в числе степеней свободы по градациям организованных факторов. Необходимость такого преобразования вызвана тем, что в расчетах факториальных дисперсий при неодинаковой численности вариант в градациях комплекса используются усредненные значения bn и n.
6. 1. Усредненное значение для расчета дисперсии по первому фактору – фактору А (коррекция неравномерности численностей градаций фактора высшей иерархии):
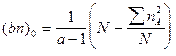 .
.

6. 2. Усредненное значение для расчета дисперсии по второму фактору – фактору В:
 , где
, где
6. 3. Усредненное значение числа наблюдений по фактору А (а - 1 – адекватно числу степеней свободы по фактору А ) – коррекция неравномерности численностей градаций фактора низшей иерархии в градациях фактора высшей иерархи – поправка на неравномерность численностей градаций фактора низшей иерархии с учетом неравномерности численностей в градациях фактора высшей иерархии (в учебнике Г. Ф. Лакина (1980, стр. 251) приведена некорректная запись:
|
|
|
 ;
;

6. 4. Усредненное значение числа наблюдений по фактору В (b – a – адекватно числу степеней свободы по фактору В ) – коррекция неравномерности градаций фактора низшей иерархи:
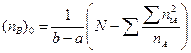 .
.
 .
.
ВНИМАНИЕ
В учебнике Г. Ф. Лакина Биометрия (Лакин, 1980, стр. 251) приведена некорректная запись! Нами исправлено!
6. 5. После чего:
 .
.
7. На следующем этапе рассчитываем факториальные и общую дисперсии.
7. 1. Дисперсия по фактору А:
 .
.
7. 2. Дисперсия по фактору В:
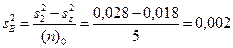 .
.
7. 3. Общая дисперсия:
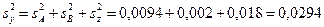 .
.
8. Далее рассчитываем силу влияния факторов.
8. 1. Сила влияния фактора А (отцовский эффект):
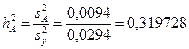 .
.
8. 2. Сила влияния фактора В, включая совместное влияние АВ (материнский эффект совместно с эффектом взаимодействия материнской и отцовской компоненты):
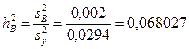 .
.
8. 3. Сила влияния неорганизованных факторов
 .
.
8. 4. Проверяем правильность расчета показателей силы влияния факторов, исходя из того, что сумма оценок доли влияния каждого из факторов должна быть равна «единице»:
 .
.
ВНИМАНИЕ!
9. В данной ситуации более корректным является расчет по следующей схеме, исключающей расчет силы влияния по фактору В и предусматривающей расчет общей «исправленной дисперсии» без учета величины или доли дисперсии по фактору В.
9. 1. Рассчитываем общую «исправленную дисперсию» как сумму «исправленной дисперсии» по фактору А и остаточной дисперсии:
 .
.
9. 2. Сила влияния фактора А (отцовский эффект) рассчитывается как:
 .
.
9. 3. Сила влияния фактора В, включая и совместное влияние АВ (материнский эффект совместно с эффектом взаимодействия отцовского и материнского факторов) не рассчитывается. Эффект от совместного влияния факторов А и В не учитывается на том основании, что один из компонентов совместного влияния, а именно фактор В, не имеет достоверного влияния.
9. 4. Сила влияния неорганизованных факторов будет вычислена как:
|
|
|
 .
.
9. 4. Проверяем правильность расчета показателей силы влияния факторов, исходя из того, что сумма оценок доли влияния каждого из факторов должна быть равна «единице»:
 .
.
Исходное условие удовлетворяется, следовательно, анализ выполнен верно.
Полученные оценки силы влияния факторов можно выразить в процентном отношении, для чего каждую из оценок умножают на 100%. В этом случае при интерпретации полученных результатов можно говорить о том, на сколько процентов изменчивость результирующего признака обусловлена влиянием каждого из учтенных факторов.
Таким образом, удается разложить общую дисперсию комплекса на составляющие её компоненты и выяснить силу влияния каждого компонента на общую изменчивость результативного признака.
Полученные оценки силы влияния факторов можно выразить в процентном отношении, для чего каждую из оценок умножают на 100%. В этом случае при интерпретации полученных результатов можно говорить о том, на сколько процентов изменчивость результирующего признака обусловлена влиянием каждого из учтенных факторов.
Таким образом, удается разложить общую дисперсию комплекса на составляющие её компоненты и выяснить силу влияния каждого компонента на общую изменчивость результативного признака.
Таблица
|
|
|


