Запишем (13) в форме кубического уравнения

. (15)

Найдем решение уравнения (15) для действительного корня K_{ру opt} с использованием формулы Кардано

K_{ру opt} = A + B, (16)

где

, , (17)

. (18)

В соотношениях (17) и (18) искомые m и p выражаются через коэффициенты уравнения (15)

, . (19)

Определим область изменения задаваемого параметра q – отношения цель/риск, соответствующую условиям (12) устойчивости принятой модели ресурсного управления по параметру K_{ру opt}.

Примем нижнее значение K_{ру opt} = 0,1, а верхнее K_{ру opt} = 1,9, т.е

0,1 ≤ K_{ру opt}≤ 1,9. (20)

Для определения границ изменения ситуационно-задаваемого параметра q воспользуемся уравнением (13), выразив из него в явном виде отношение цель/риск q

. (21)

Подставив в выражение (21) K_ру = 0,1, получим нижнюю границу параметра q, значению K_ру = 1,9 соответствует верхняя граница искомого параметра q

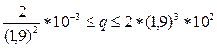. (22)

С учетом корректности постановки задачи ресурсной оптимизации (14) ограничим область изменения параметра q на интервале

1 < q < 10³. (23)

Малые интервальные оценки (23) параметра q соответствуют рискованным ситуациям ресурсного управления, большие – управлению при малых рисках.

Для примера получения численной оценки K_{ру opt} по соотношениям (16) – (19) выберем значение параметра

q = 3, (24)

соответствующее управлению ресурсами предприятия в рисковой ситуации

1 < q < 10. (25)

Для q = 3 (24) параметры p и m (19) равны

, (26)

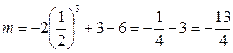. (27)

Подставив найденные значения p и m (26), (27) в выражение (18), вычислим параметр M

. (28)

Определим параметры A и B (17) по найденным значениям m (27) и M (28)

,

(29)

.

Подставив найденные параметры A и B (29) в выражение (16) для оптимальной интенсивности управления ресурсами предприятия в рисковой ситуации, получим

K_{ру opt} = 1,65 – 1,1 = 0,55. (30)

Выводы.

1. При эффективной организации функции контроля оптимальная интенсивность управления ограниченными ресурсами предприятия определяется ситуационно-оцениваемым параметром – отношением цель/риск – q. Для моделирования ситуаций практической деятельности ресурсного управления на предприятии целесообразно ввести три возможных случая:

- больших рисков – 0,1 < q < 10,

- средних рисков – 10 < q < 10²,

- малых рисков – 10² < q < 10³.

2. Численные значения оптимальной интенсивности ресурсного управления должны выбираться с учетом условий устойчивости модели деятельности предприятия, учитывающей функцию «контроль» за счет организации отрицательной обратной связи.

3. Найденное значение оптимальной интенсивности ресурсного управления является определяющим параметром структурной схемы модели и уравнений ее динамики, доставляющим минимальное значение прогнозируемому критерию эффективности управления, учитывающему параметры запланированного изменения целевой функции и интенсивности рисков.

4. С уменьшением интенсивности рисков значение оптимальной интенсивности ресурсного управления K_{ру opt} увеличивается. В рассмотренной ситуации больших рисков оно меньше единицы, т.е. не совпадает с оптимальным значением интенсивности ресурсного управления, найденным по критерию максимального быстродействия модели (K_o = 1), соответствующего условиям бесконечной степени устойчивости [3] (см. рис. 3.36 п. 3.2.4).

 

Ситуационный анализ целевой динамики на эффективность ресурсного управления предприятием

Задача 3.

Оценить ситуационное влияние внешних сред на эффективность ресурсного управления предприятием.

Этапы решения.

1. Определяем ресурсную ситуацию на предприятии экспертным выбором одной из трех возможных:

ситуация 1 – существенно ограниченные ресурсы деятельности и управления;

ситуация 2 –ограниченные ресурсы деятельности и управления;

ситуация 3 – условно-ограниченные ресурсы деятельности и управления.

Примем результатом экспертного выбора ситуацию 2 наличия на предприятии ограниченных ресурсов деятельности (материальных, финансовых, трудовых) и управления – менеджмента.

2. Формируем критерий эффективности ресурсного управления.

2.1. Выбираем под ситуацию 2 типовой закон ресурсного управления в форме ТЗРУ 2 [3] (см.п. 3.2.2.1) – управление с учетом скорости изменения целевой функции, например желаемой – запланированной прибыли с течением времени работы предприятия.

2.2. Записываем в формализованном виде критерий эффективности при ситуационно-выбранном законе ресурсного управления с учетом обобщенного рискового возмущения (угроз) внешних сред выражения ((1) – (6), задача 2).

. (1)

В выбранном квадратическом критерии качества управления (1), показывающем, насколько результаты деятельности предприятия y(i) в установившемся режиме его работы отличаются от запланированных x(i)

, (2)

способствующие возможности внешних сред определяют величину «скорости» изменения целевой функции , препятствующие возмущения внешних сред отражаются интенсивностью – дисперсией рисков (угроз) N_v, а возможности ресурсного управления в принятой ситуации 2 – параметром K_ру, характеризующим интенсивность использования всех видов ресурсов предприятия при выбранном законе управления ими – ТЗРУ 2.

2.3. Преобразуем критерий эффективности ресурсного управления (1) к расчетному виду, положив для номинального – нормального режима работы предприятия коэффициент преобразования измерителя целевого рассогласования K_r =1, что отражает высокую эффективность реализации функции «контроль» на предприятии, и введя обобщенный ситуационный параметр

(3)

как отношение цель/риск, характеризующий относительные возможности и риски-угрозы внешних сред, тогда

. (4)

В критерии качества ресурсного управления (4) интенсивность использования ресурсов – параметр K_ру выбирается из области устойчивости математической модели ресурсного управления предприятием по ТЗРУ 2 [3] (см. п.3.2.3.2).

0 < K_ру < 2.

При оптимальном выборе интенсивности использования ресурсов

K_ру = K_{ру opt}

существует однозначная связь K_{ру opt}(q) для заданного экспертно-оцененного обобщенного ситуационного параметра цель/риск внешних сред – q (соотношение (15), (16), задача 2 для ТЗРУ 2), например, для рисковой ситуации q = 3 значение K_{ру opt} = 0,55 (результат (30), задача 2).

Запишем критерий (4) для оптимальных соотношений параметров q и K_{ру opt}

. (5)

После выполнения числовых преобразований

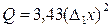, (6)

или

. (7)

Тогда в соотношении (2) для результатов деятельности предприятия y(i)

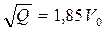. (8)

Соотношение (8) характеризует отклонение результатов деятельности предприятия y(i) от запланированных x(i) в установившемся режиме его функционирования по отношению к использованию всех видов ресурсов. Возможности внешней среды отражаются параметром V₀ – «скоростью» изменения целевой функции при линейной динамике ее нарастания или убывания. «Весовой» коэффициент, в данном случае 1,85, определяется интенсивностью ресурсного управления при выбранном ТЗРУ (параметром K_ру) и отношением цель/риск (параметром q).

3. Оцениваем тенденцию влияния возможностей внешней среды на величину целевых отклонений.

3.1. Абсолютные оценки

Так как «весовой» коэффициент, в данном случае 1,85, в выражении (8) является безразмерным в силу относительности параметров K_ру и q в соотношениях (4) и (5), то оценки целевых отклонений оказываются полученными в абсолютных единицах, если «скорости» изменения целевых функций V₀ также определяются в абсолютных единицах, совпадающих по единицам измерения с запланированными целевыми функциями x(i) и результатами деятельности предприятия y(i). Для удовлетворения этому требованию необходимо в выражении для первой конечной разности

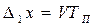(9)

линейно нарастающей целевой функции

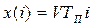, (10)

где i = 0, 1, 2, 3, …. отсчитывают дискретные интервалы времени работы предприятия величиной T_П (дни, недели, месяцы, годы и т.д.).

В выражениях (9) и (10) величина скорости изменения целевой функции V имеет принятые единицы измерения относительно планируемого периода, например, если под целевой функцией x(i) понимается планируемая прибыль, измеряемая в у.е., то единицами измерения скорости ее изменения являются , где в знаменателе отражаются периоды планирования. Величина T_П в соотношениях (9) и (10)отражает периоды времени «контроля», т.е. измерения (получения оценок) реальной прибыли y(i), полученной в результате деятельности предприятия. В общем случае планируемые и контрольные интервалы времени могут не совпадать. Для получения состоятельных оценок «скорости» V₀ изменения целевой функции в (8) синхронизируем интервалы времени планирования и контроля, т.е. выберем их одинаковыми

. (11)

В этом случае численная оценка V₀ в (11) будет совпадать со значением V в (9) и (10).

Пример.

Пусть множество возможных экспертных скоростей изменения V планируемой прибыли в (9) и (10), обусловленное возможностями внешней среды и ограниченными ресурсами предприятия, принимает значения

.

выберем период контроля эффективности работы предприятия – измерения реальной прибыли, целевых рассогласований и целевых отклонений (8) T_П в (9) и (10) равным периоду планирования

. (12)

На основании (12) численная оценка первой конечной разности целевой функции V₀ (11) равна

, (13)

но выражена в [ у.е. ] измерения.

При выполнении условия синхронизации (12) множество конечных разностей «скоростей» изменения целевой функции V₀ принимает значения

.

На основании (8) множество соответствующих V₀ значений целевых отклонений равно

.

Множество целевых отклонений (2) характеризует отклонение реальной прибыли предприятия от запланированной

(14)

по окончании пускового периода его деятельности.

Так за год работы после окончания пускового периода множество планируемой прибыли X₁, соответствующее множествам V и V₀, составит

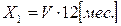, (15)

.

Множество реальной прибыли равно

, (16)

.

3.2. Относительные оценки

Относительные оценки используются при информационной неопределенности в исходных данных для выявления тенденций влияния факторных возможностей внешних сред, отраженных в параметрах целевых функций и законах их изменения, на величины целевых отклонений, а также для соблюдения условия конфиденциальности – защиты исходной и расчетной информации об эффективности деятельности предприятия.

Переход от абсолютных оценок к относительным в множествах исходных данных скоростей изменения целевых функций V и V₀ осуществляется делением каждого значения соответствующего множества на наибольшее по абсолютной величине значение его элемента.

Пример.

Приведем относительные значения планируемых показателей и оценок результатов деятельности предприятия по примеру, рассмотренному в п.3.1.

Относительное множество скоростей изменения целевых функций

V {0,25; 0,5; 0,75; 1}.

Относительное множество конечных разностей (приращений) как «скоростей» изменения целевых функций для условий временной синхронизации

V₀ {0,25; 0,5; 0,75; 1}.

Относительное множество целевых отклонений рассчитывается в соответствии с выражением (8)

{0,46; 0,93; 1,39; 1,85}.

 

Относительное множество планируемой прибыли по окончании 1 года установившегося режима работы предприятия рассчитывается по формуле 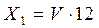, (17)

где V – относительное множество скоростей изменения целевых функций, безразмерное число 12 соответствует числу месяцев в году.

На основании (17)

X₁ {3; 6; 9; 12}.

Относительное множество реальной прибыли за 1 год установившегося режима работы предприятия рассчитывается по (16), где под X₁ понимается относительное множество планируемой прибыли, а за - относительное множество целевых отклонений,

Y₁ {2,5; 5,1; 7,6; 10,2}.

По определению все элементы относительных множеств являются безразмерными величинами.

Выводы.

1. При линейной динамике целевых функций и согласованным с ней законом ресурсного управления ТЗРУ 2 «по скорости» изменения целевой функции целевые отклонения в установившемся режиме работы предприятия факторно определяются интенсивностью использования ресурсов, соотношением факторов внешних сред по возможностям и угрозам - отношением цель/риск и пропорциональны скорости изменения целевой функции. При этом целевые отклонения всегда отличны от нуля, т.е. результаты деятельности предприятия отличаются от запланированных на конечную величину.

2. Пропорциональный характер зависимости между целевым отклонением и «скоростью» V₀ изменения целевой функции в форме соотношения (8) имеет место для асимптотического случая высокой эластичности внешних сред, например, рынка, т.е. при жесткой их реакции на запланированные и реальные действия предприятия, что проявляется в сохранении постоянного значения отношения q – цель/риск в выражениях (4)-(8) (во сколько раз увеличивается «скорость» изменения целевой функции, во столько же раз возрастают угрозы со стороны внешних сред, например, со стороны конкурентов). Ситуация слабой реакции со стороны внешних сред требует пересчета отношения цель/риск – q с увеличением скорости изменения целевой функции V₀ и расчетов целевых отклонений по исходному выражению (4).

3. Возможности внешних сред по повышению эффективности деятельности предприятия ограничиваются инерционным характером выбранного закона управления всеми видами ресурсов – ТЗРУ 2. Для устранения (обнуления) целевых отклонений при линейной динамике целевых функций необходим переход к ТЗРУ 3 – по «ускорению»изменения целевой функции, что требует больших ресурсных возможностей, т.к. ему соответствуют ресурсные затраты во времени с отличным от нуля ускорением.

Задание.

Построить зависимости X₁ (V), (V₀), Y₁ (V).

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: