 |
9.3.2 Графический метод. Данные, полученные при продольном точении конструкционной стали 45 ( МПа) на токарно-винторезном
|
|
|
|
9. 3. 2 Графический метод
Графический метод имеет широкое приложение, но дает точные результаты только в том случае, когда экспериментальные точки достаточно плотно группируются вдоль прямой линии. Чтобы не рассчитывать логарифмы величин х и у, экспериментальные точки при графической обработке наносят в двойной логарифмической системе координат, где по осям от исходной точки в некотором масштабе откладываются отрезки, равные десятичным логарифмам ряда чисел. Таким образом, на логарифмической шкале расстояние от метки 1 к метке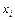 
равняется в избранном масштабе 
.
Примечание. Для построения логарифмической сетки можно использовать любую шкалу логарифмической линейки.
Пример. Нужно установить зависимость главной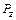 
и радиальной 
составляющих силы резания от подачи.
1. Для установления зависимостей главной 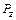и радиальной составляющих силы резания от подачи проводят серию опытов при 
и 
. При каждом опытном подходе по показаниям приборов и тарировочному графику определяют измеряемые силы 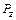и .
Данные и результаты опытов вносят в журнал наблюдений (табл. 9. 1).
Таблица 9. 1
Данные, полученные при продольном точении конструкционной стали 45 ( МПа) на токарно-винторезном
станке модели 16К20
|
Вариант |
Условия процесса резания ( мм, Ø 100 мм, об/мин) | |||||
 , мм/об
| 0, 10 | 0, 15 | 0, 20 | 0, 25 | 0, 3 | 0, 4 |
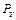 , Н
| ||||||
 , Н
| ||||||
9. 4 ПОСТРОЕНИЕ ГРАФИКОВ В ДВОЙНЫХ ЛОГАРИФМИЧЕСКИХ
КООРДИНАТАХ
9. 4. 1 Общая методика построения логарифмических шкал
Построение графиков необходимо начать с построения логарифмических шкал.
|
|
|
Общее уравнение логарифмических шкал имеет вид:
, (9. 10)
где 
– длина отрезка шкалы, которая соответствует значению переменной 
, мм; 
– модуль соответствующей шкалы; – текущее значение переменной величины;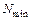 
– минимальное значение переменной, которое выбирают за начало шкалы.
Необходимо учесть, что на логарифмической шкале нельзя показать точку, которая отвечает 
. Значения переменной, которые отвечают началу и концу логарифмической шкалы, отличаются в С раз, где С – основание логарифмов. Если 
, то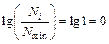 
.
Аналогично при после следующей формулы поставить (, ) 
и 
. Таким образом, модуль логарифмической шкалы переменной – это отрезок между значениями 1…10, 10…100, 100…1000 и т. д. При определенной длине шкалы L ее модуль рассчитывают по формуле:
.
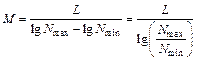Логарифмические шкалы могут строиться несколькими способами.
1. Копированием стандартных логарифмических шкал, например, логарифмической линейки, на которой имеется три логарифмические шкалы: основная шкала, модуль которой равняется 
мм, шкала квадратов, модуль которой равняется – 
мм и шкала кубов – 
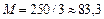мм.
2. Расчетным путем целесообразно строить шкалы, когда принятое значение модуля шкалы существенно отличается от тех, которые имеются на логарифмической линейке или если предварительно установлены определенные размеры шкал графика.
При построении логарифмических шкал следует помнить, что они не могут начинаться с нуля. Начало координат на логарифмическом графике всегда отвечает положительным значениям обеих переменных.
Последовательность построения графиков в логарифмической системе координат и методику определения неизвестных параметров математических моделей рассмотрим непосредственно на конкретном примере.
|
|
|
