 |
9.4.2 Построение логарифмических шкал для
|
|
|
|
9. 4. 2 Построение логарифмических шкал для
графика расчетным методом
Математические модели общего вида составляющих силы резания:
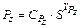 , (9. 11)
, (9. 11)
 .
.
Неизвестными параметрами этих моделей являются показатели степени 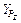 ,
,  и коэффициенты пропорциональности
и коэффициенты пропорциональности  ,
, 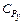 . Неизвестные показатели степени определяются по графику зависимости составляющих силы резания
. Неизвестные показатели степени определяются по графику зависимости составляющих силы резания 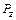 и
и  от подачи по формулам:
от подачи по формулам:
 ,
,
 ,
,
где 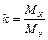 – отношение модуля шкалы абсцисс и модуля шкалы ординат (масштабный коэффициент); a и a1 – соответственно угол наклона графика зависимости главной
– отношение модуля шкалы абсцисс и модуля шкалы ординат (масштабный коэффициент); a и a1 – соответственно угол наклона графика зависимости главной 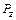 и радиальной
и радиальной 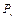 составляющей силы резания к оси абсцисс.
составляющей силы резания к оси абсцисс.
Для построения графика предварительно принимаем размеры отрезков шкал: абсцисс, например,  =160 мм, ординат
=160 мм, ординат  =140 мм. Соответствующие модули шкал рассчитываем по общей формуле:
=140 мм. Соответствующие модули шкал рассчитываем по общей формуле:
 . (9. 12)
. (9. 12)
Для построения шкал расширяем диапазон изменения аргументов и функции, а именно принимаем  = 0, 05 мм/об;
= 0, 05 мм/об; 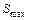 = 0, 5 мм/об;
= 0, 5 мм/об; 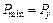 = 50 Н;
= 50 Н;  = 400 Н.
= 400 Н.
Для принятых значений переменных величин рассчитываем модули шкал:
 [мм]. (9. 13)
[мм]. (9. 13)
Принимаем  = 160 мм.
= 160 мм.
 [мм]. (9. 14)
[мм]. (9. 14)
Принимаем 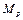 = 155 мм.
= 155 мм.
Для построения шкалы абсцисс рассчитаем положение целочисленных значений аргумента с применением зависимости:
 . (9. 15)
. (9. 15)
Все результаты расчетов сводим в таблицы.
Таблица 9. 2
Исходные данные для построения шкалы абсцисс
| S, мм/об | 0, 05 | 0, 10 | 0, 15 | 0, 2 | 0, 25 | 0, 3 | 0, 4 | 0, 5 |
| l, мм | 48, 16 | 76, 34 | 96, 33 | 111, 8 | 124, 5 | 144, 5 |
Таблица 9. 3
Исходные данные для построения шкалы ординат
| Р, Н | |||||||||
| l, мм | 27, 3 | 46, 7 | 74, 0 | 93, 3 | 108, 3 | 120, 6 | 131, 0 | 139, 98 |
|
|
|
Таблица 9. 4
Исходные данные для построения графика составляющих силы резания от подачи
| Рz, Н | ||||||
| l, мм | 69, 3 | 98, 9 | 104, 2 | 116, 0 | 135, 6 | |
| Рy, Н | ||||||
| l, мм | 45, 3 | 58, 9 | 66, 9 | 80, 4 |
По данным, которые приведены в табл. 9. 2…9. 4, строим график зависимости составляющих силы резания от подачи.
Определяем неизвестные показатели степени:
 . (9. 16)
. (9. 16)
Принимаем  =0, 71.
=0, 71.
 . (9. 17)
. (9. 17)
Принимаем 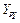 =0, 74.
=0, 74.
Определяем коэффициенты пропорциональности:
 . (9. 18)
. (9. 18)
Результаты расчетов приведены в табл. 9. 5.
Таблица 9. 5
Определение коэффициентов пропорциональности 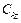
| S, мм/об | 0, 10 | 0, 15 | 0, 20 | 0, 25 | 0, 3 | 0, 4 |
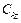
| 730, 7 | 736, 8 | 749, 2 | 752, 3 | 718, 7 |
 . (9. 19)
. (9. 19)
Принимаем 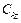 =734, 2.
=734, 2.
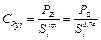 . (9. 20)
. (9. 20)
Результаты расчетов приведены в таблице 9. 6.
Таблица 9. 6
Определение коэффициентов пропорциональности 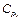
| S, мм/об | 0, 10 | 0, 15 | 0, 20 | 0, 25 | 0, 3 | 0, 4 |
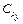
| 318, 7 | 317, 5 | 322, 5 | 334, 7 | 329, 0 | 325, 1 |
 . (9. 21)
. (9. 21)
Принимаем 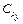 =324, 6. В результате расчетов получены следующие математические модели (рис. 9. 15).
=324, 6. В результате расчетов получены следующие математические модели (рис. 9. 15).
 ,
,
 . (9. 22)
. (9. 22)
9. 4. 3 Построение математических моделей с применением
стандартных логарифмических шкал
Для построения графика используем логарифмические шкалы, которые имеются на логарифмической линейке, и соответствующий график (рис. 9. 15).
Определяем неизвестные показатели степени:
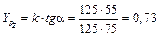 .
.

|
Рис. 9. 15. График зависимости составляющих силы
резания  и и  от подачи S от подачи S
|
Принимаем  =0, 73.
=0, 73.
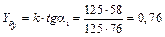 .
.
Принимаем  =0, 76.
=0, 76.
Определение коэффициентов пропорциональности
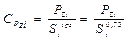 . (9. 23)
. (9. 23)
Результаты расчетов приведены в табл. 9. 7.
Таблица 9. 7
Определение коэффициентов пропорциональности 
|
|
|
| S, мм/об | 0, 10 | 0, 15 | 0, 20 | 0, 25 | 0, 3 | 0, 4 |
| 751, 8 | 758, 9 | 760, 9 | 770, 6 | 770, 6 |
 .
.
Принимаем 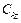 =757, 4.
=757, 4.
 . (9. 24)
. (9. 24)
Таблица 9. 8
Определение коэффициентов пропорциональности 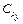
| S, мм/об | 0, 10 | 0, 15 | 0, 20 | 0, 25 | 0, 3 | 0, 4 |
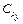
| 333, 8 | 329, 8 | 333, 0 | 344, 1 | 337, 1 | 331, 1 |
 . (9. 25)
. (9. 25)
Принимаем 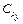 =334, 3.
=334, 3.
В результате расчетов получены следующие математические модели для составляющих силы резания:
 ,
,
 . (9. 26)
. (9. 26)
Проверяем работоспособность математических моделей (9. 22) и (9. 26 )
Для этого выполним расчеты составляющих силы резания при исходных значениях подачи. Результаты расчетов приведены в табл. 9. 9.
Таблица 9. 9
Расчет составляющих силы резания по
математическим моделям
| S, мм/об | 0, 10 | 0, 15 | 0, 20 | 0, 25 | 0, 3 | 0, 4 |
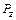 , Н , Н
| ||||||
 , Н , Н
| ||||||
 , Н , Н
| 143, 2 | 190, 9 | 234, 2 | 274, 4 | 312, 3 | 383, 1 |
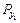 , Н , Н
| 59, 1 | 79, 7 | 98, 7 | 116, 4 | 132, 2 | 164, 8 |
 , Н , Н
| 141, 0 | 189, 6 | 233, 9 | 275, 3 | 314, 5 | 388, 0 |
 , Н , Н
| 58, 1 | 79, 1 | 98, 4 | 116, 6 | 133, 9 | 166, 6 |
Определяем погрешность расчетов по формуле:
 , (9. 27)
, (9. 27)
где 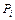 – экспериментальное значение составляющей силы резания;
– экспериментальное значение составляющей силы резания; 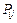 – рассчитанное значение составляющей силы резания по математической модели.
– рассчитанное значение составляющей силы резания по математической модели.
Результаты расчетов приведены в табл. 9. 10.
Таблица 9. 10
|
|
|


