 |
Определение погрешности расчетов
|
|
|
|
Определение погрешности расчетов
| S, мм/об | 0, 10 | 0, 15 | 0, 20 | 0, 25 | 0, 3 | 0, 4 |
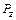 , Н , Н
| ||||||
 , % , %
| 2, 29 | 0, 47 | 0, 34 | 2, 0 | 2, 41 | 2, 16 |
 , % , %
| 0, 7 | 0, 21 | 0, 45 | 1, 68 | 1, 72 | 3, 47 |
 , Н , Н
| ||||||
 , % , %
| 1, 9 | 2, 18 | 0, 71 | 3, 0 | 1, 33 | 0, 12 |
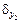 , % , %
| 0, 17 | 1, 41 | 0, 41 | 2, 83 | 0, 81 | 0, 97 |
Вывод: погрешность расчетов составляющих силы резания 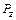 и
и  не превышает
не превышает 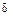 = 3, 5% (табл. 9. 10). Это свидетельствует о возможности использования математических моделей (9. 22) и (9. 26) для определения составляющих силы резания
= 3, 5% (табл. 9. 10). Это свидетельствует о возможности использования математических моделей (9. 22) и (9. 26) для определения составляющих силы резания 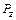 и
и  в диапазоне изменения подачи
в диапазоне изменения подачи  = (0, 1¸ 0, 4) мм/об.
= (0, 1¸ 0, 4) мм/об.
9. 5 МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Метод основан на том положении, что наиболее точная аппроксимация любой функции  будет в том случае, если сумма квадратов отклонений расчетных значений
будет в том случае, если сумма квадратов отклонений расчетных значений  от экспериментальных
от экспериментальных  является минимальной, то есть:
является минимальной, то есть:
 . (9. 28)
. (9. 28)
В случае определения неизвестных, например,  и
и  прологарифмируем выражение
прологарифмируем выражение 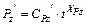 , что позволяет представить функционал, характеризующий силу резания в виде линейной зависимости относительно параметров
, что позволяет представить функционал, характеризующий силу резания в виде линейной зависимости относительно параметров  и
и  :
:
 .
.
Тогда условие (9. 28) будет иметь вид:
 . (9. 29)
. (9. 29)
Минимум функции Е можно определить из системы уравнений: 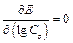 и
и  . После дифференцирования и соответствующих преобразований получаем систему уравнений относительно неизвестных
. После дифференцирования и соответствующих преобразований получаем систему уравнений относительно неизвестных  и
и 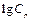 :
:
 (9. 30)
(9. 30)
из которых определяются неизвестные для отдельных зависимостей:
 ; (9. 31)
; (9. 31)
 , (9. 32)
, (9. 32)
где n – число опытов в соответствующей серии.
Параметры другой отдельной зависимости находим аналогично. Для нахождения численных значений  ,
,  и
и  в обобщенном уравнении решается общая задача, то есть задача определения неизвестных для обеих серий опытов. Путем логарифмирования степенная зависимость подана в виде линейного полинома
в обобщенном уравнении решается общая задача, то есть задача определения неизвестных для обеих серий опытов. Путем логарифмирования степенная зависимость подана в виде линейного полинома
|
|
|
 . (9. 33)
. (9. 33)
Аналогично предыдущему примеру после дифференцирования суммы квадратов отклонений и соответствующих преобразований получим систему уравнений:
 (9. 34)
(9. 34)
где n – общее количество опытов.
Эта система является системой линейных уравнений с постоянными коэффициентами:
 (9. 35)
(9. 35)
Ее легко можно решить методом Гаусса.
Пример. 1. Для получения обобщенной эмпирической зависимости 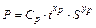 занесем в табл. 9. 11 результаты.
занесем в табл. 9. 11 результаты.
Таблица 9. 11
Пример расчета коэффициентов системы уравнений (9. 35)
|
Номер опыта |
S, мм/об |
t, мм |
, Н |
n |
lg(t) |
lg(s) |
lg(P) |
lg(t) | lg(t)2 |
lg(S)× lg(t) |
lg(P) × lg(t) |
lg(s) |
lg(t)× lg(s) | lg(s)2 |
lg(P)× lg(s) |
Р, Н | |
| 0, 3 | 1, 0 | 0, 000 | -0, 523 | 3, 322 | 0, 000 | 0, 000 | 0, 000 | 0, 000 | -0, 523 | 0, 000 | 0, 273 | -1, 737 | 2095, 7 | 18, 4 | |||
| 0, 3 | 2, 0 | 0, 301 | -0, 523 | 3, 602 | 0, 301 | 0, 091 | -0, 157 | 1, 084 | -0, 523 | -0, 157 | 0, 273 | -1, 883 | 4076, 8 | 5899, 5 | |||
| 0, 3 | 3, 0 | 0, 477 | -0, 523 | 3, 792 | 0, 477 | 0, 228 | -0, 249 | 1, 809 | -0, 523 | -0, 249 | 0, 273 | -1, 983 | 6016, 8 | 33550, 5 | |||
| 0, 1 | 2, 0 | 0, 301 | -1, 000 | 3, 255 | 0, 301 | 0, 091 | -0, 301 | 0, 980 | -1, 000 | -0, 301 | 1, 000 | -3, 255 | 1788, 5 | 133, 2 | |||
| 0, 3 | 2, 0 | 0, 301 | -0, 523 | 3, 519 | 0, 301 | 0, 091 | -0, 157 | 1, 059 | -0, 523 | -0, 157 | 0, 273 | -1, 840 | 4076, 8 | 603431, 0 | |||
| 0, 5 | 2, 0 | 0, 301 | -0, 301 | 3, 778 | 0, 301 | 0, 091 | -0, 091 | 1, 137 | -0, 301 | -0, 091 | 0, 091 | -1, 137 | 5980, 1 | 396, 9 | |||
| Сумма | 1, 681 | -3, 393 | 21, 269 | 1, 681 | 0, 590 | -0, 956 | 6, 070 | -3, 393 | -0, 956 | 2, 184 | -11, 836 |
| 643429, 4 | ||||
|
| a11 | a12 | a13 | b1 | a21 | a22 | a23 | b2 | a31 | a33 | a32 | b3 |
| 214476, 5 | |||
| Коэффициенты уравнений системы |
|
| |||||||||||||||
На основании полученных расчетных данных составим систему уравнений:
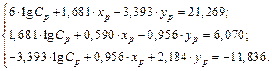 (9. 36)
(9. 36)
Выполняя деление каждого уравнения на коэффициент, записываем систему в матричной форме:
 .
.
Используем метод Гаусса:  ,
,  ,
,  и получаем эмпирическую зависимость
и получаем эмпирическую зависимость 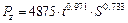 .
.
Оценка адекватности полученного уравнения и доверительный интервал величины силы, рассчитанной по полученным эмпирическим уравнениям.
Полученное эмпирическое уравнение необходимо проверить на адекватность экспериментальным данным. Как критерий в этом случае можно использовать критерий Фишера:
 , (9. 37)
, (9. 37)
где  – дисперсия адекватности, которая определяется по формуле:
– дисперсия адекватности, которая определяется по формуле:
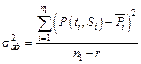 ; (9. 38)
; (9. 38)
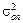 – дисперсия эксперимента;
– дисперсия эксперимента;  – количество неизвестных коэффициентов в эмпирическом уравнении;
– количество неизвестных коэффициентов в эмпирическом уравнении;
 , (9. 39)
, (9. 39)
где 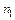 – общее количество опытов;
– общее количество опытов;  – количество повторений каждого опыта;
– количество повторений каждого опыта; 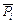 – математическое ожидание величины силы резания.
– математическое ожидание величины силы резания.
Величина критического значения функции Фишера определяется по таблицам или может быть вычислена при:
– заданном уровне значимости и известных степенях свободы;
– дисперсии адекватности эмпирического уравнения;
– объединенной дисперсии плана эксперимента.
В рассмотренном примере (табл. 9. 11):
 ;
;  ;
;  ;
; 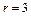 ;
;  ;
; 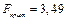 (табл. А. 1);
(табл. А. 1);  214476 Н2;
214476 Н2; 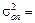 132116 Н2;
132116 Н2;
 .
.
Так как критерий Фишера в рассмотренном примере удовлетворяется, то адекватность полученной эмпирической зависимости доказана.
Поскольку определенное эмпирическое уравнение отображает влияние режима резания на силу с некоторой погрешностью, то для практического использования этой зависимости необходимо оценить доверительный интервал, то есть интервал, в котором наиболее вероятно будет находиться сила резания в реальном процессе.
Доверительный интервал полученной зависимости можно оценить, зная среднее квадратичное отклонение в заданной выборке. Для этого определяется среднее квадратичное отклонение результатов опытов с одинаковыми режимами резания:
 , (9. 40)
, (9. 40)
где К – общее количество повторений опытов с одинаковым режимом резания; 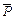 – математическое ожидание величины силы резания в этих опытах.
– математическое ожидание величины силы резания в этих опытах.
|
|
|
Тогда доверительный интервал  определяется:
определяется:
 , (9. 41)
, (9. 41)
где  – величина распределения Стьюдента при числе степеней свободы
– величина распределения Стьюдента при числе степеней свободы  и доверительной значимости a (из таблиц приложения А). В рассмотренном примере получаем следующие результаты (табл. 9. 12):
и доверительной значимости a (из таблиц приложения А). В рассмотренном примере получаем следующие результаты (табл. 9. 12):
Таблица 9. 12
|
|
|




