Среднее квадратическое отклонение

по х:

по у:

Эта величина называется также стандартным отклонением, выражается в тех же единицах, что и величины, полученные в результате эксперимента. И зачастую оказывается более удобной характеристикой, чем дисперсия. Чем слабее варьирует признак, тем меньше среднее квадратическое отклонение.

Коэффициент вариации

Коэффициент вариации необходим для сравнения изменчивости признаков, выраженных разными единицами. Дисперсия и среднее квадратическое отклонение – величины абсолютные, именованные, выражаемые в тех же единицах, что и характеризуемый ими признак.

Коэффициент вариации – относительный показатель, представляет процентное отношение среднего квадратического отклонения к математическому ожиданию

по х:

по у:

Нормированное отклонение

Нормированное отклонение – показатель, представленный отклонением той или иной величиной от математического ожидания, отнесённое к величине среднего квадратического отклонения:

по х:

по у:

Коэффициент корреляции

Коэффициент корреляции характеризует степень линейной зависимости (степень связи) между величинами х и у.

Вычисляется по формуле:

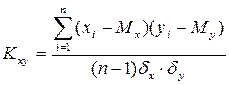
Или

Значение К_ху изменяется в пределах от -1 до +1. Если значение К_ху > 0, то корреляция положительная (с ростом х значение у увеличивается), если К_ху < 0, то корреляция отрицательная (с ростом х значение у уменьшается).

При значении | К_ху | близком к 1 существует линейная зависимость между х и у, т.е. 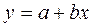, знак корреляции совпадает со знаком коэффициента .

Определение значимости коэффициента корреляции

Уровень значимости коэффициента корреляции может быть определён по критерию Стьюдента:

Если , где - уровень значимости =0.95, а - число степеней свободы =n-2, то можно утверждать, что между х и у существует линейная зависимость, в противном случае – линейная зависимость отсутствует.

Значение T _табл выбирается по таблице значений критерия Стьюдента.

Отчет выполненной данной работы содержит:

1. Содержательную постановку задачи (выбор значений x и у, полученных в результате эксперимента)

2. Математическую постановку задачи (функции, по которым проводились расчеты)

3. Блок-схему алгоритма решения задач

4. Программу на алгоритмическом языке

5. Результат работы программы

6. Вывод по расчётам

7. Расчет, полученный в Excel

Содержательную постановку задачи каждый студент выполняет самостоятельно.

Пример выполнения работы

Провести расчет на Qbasic и в Excel.

Содержательная постановка задачи

Проведён эксперимент по определению зависимости коэффициента активности от ионной силы раствора.

Для этих величин необходимо рассчитать все характеристики случайных величин. Сделать вывод о наличии или отсутствии линейной зависимости

№	Ионная сила раствора Х(i)	Коэффициент активности Y(i)
	0,001 0,002 0,005 0,01 0,04 0,05 0,1 0,2 0,3 0,4 0,5	0,98 0,97 0,95 0,92 0,9 0,84 0,81 0,8 0,81 0,82 0,84

Табличные значения коэффициента Стьюдента = 2.201

Таблица значений критерия Стьюдента

f	q
0.80	0.90	0.95	0.98	0.99	0.995	0.998	0.999
	3.0770	6.3130	12.7060	31.820	63.656	127.656	318.306	636.619
	1.8850	2.9200	4.3020	6.964	9.924	14.089	22.327	31.599
	1.6377	2.35340	3.182	4.540	5.840	7.458	10.214	12.924
	1.5332	2.13180	2.776	3.746	4.604	5.597	7.173	8.610
	1.4759	2.01500	2.570	3.649	4.0321	4.773	5.893	6.863
	1.4390	1.943	2.4460	3.1420	3.7070	4.316	5.2070	5.958
	1.4149	1.8946	2.3646	2.998	3.4995	4.2293	4.785	5.4079
	1.3968	1.8596	2.3060	2.8965	3.3554	3.832	4.5008	5.0413
	1.3830	1.8331	2.2622	2.8214	3.2498	3.6897	4.2968	4.780
	1.3720	1.8125	2.2281	2.7638	3.1693	3.5814	4.1437	4.5869
	1.363	1.795	2.201	2.718	3.105	3.496	4.024	4.437
	1.3562	1.7823	2.1788	2.6810	3.0845	3.4284	3.929	4.178
	1.3502	1.7709	2.1604	2.6503	3.1123	3.3725	3.852	4.220
	1.3450	1.7613	2.1448	2.6245	2.976	3.3257	3.787	4.140
	1.3406	1.7530	2.1314	2.6025	2.9467	3.2860	3.732	4.072
	1.3360	1.7450	2.1190	2.5830	2.9200	3.2520	3.6860	4.0150
	1.3334	1.7396	2.1098	2.5668	2.8982	3.2224	3.6458	3.965
	1.3304	1.7341	2.1009	2.5514	2.8784	3.1966	3.6105	3.9216

Значения критерия Стьюдента (t-критерия) для различного уровня значимости q и числа степеней свободы f (f = n-2 или n, n-число опытов).

1. Математическое ожидание: 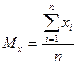и

2. Дисперсия: и

3. Среднее квадратическое отклонение: и

4 Коэффициент вариации: и

5. Нормированное отклонение: и

6. Коэффициент корреляции:

7. Критерий Стьюдента:

БЛОК-СХЕМА

ПРОГРАММА НА ЯЗЫКЕ QBASIC

CLS

n = 11

INPUT "Введите Коэффициент Стьюдента="; tt

DIM x(1 TO n), y(1 TO n), tx(1 TO n), ty(1 TO n)

DATA 0.001, 0.002, 0.005, 0.01, 0.04, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5

FOR i = 1 TO n

READ x(i)

NEXT i

DATA 0.98, 0.97, 0.95, 0.92, 0.9, 0.84, 0.81, 0.8, 0.8, 0.81, 0.82, 0.84

FOR i = 1 TO n

READ y(i)

NEXT i

mx = 0: my = 0

FOR i = 1 TO n

mx = mx + x(i)

my = my + y(i)

NEXT i

mx = mx / n: my = my / n

dx = 0: dy = 0: S = 0

FOR i = 1 TO n

dx = dx + (x(i) - mx) ^ 2

dy = dy + (y(i) - my) ^ 2

S = S + (x(i) - mx) * (y(i) - my)

NEXT i

dx = dx / (n - 1): dy = dy / (n - 1)

CKOx = SQR(dx): CKOy = SQR(dy)

Vx = CKOx * 100 / mx: Vy = CKOy * 100 / my

FOR i = 1 TO n

tx(i) = (x(i) - mx) / CKOx

ty(i) = (y(i) - my) / CKOy

NEXT i

Kxy = S / ((n - 1) * CKOx * CKOy)

tr = ABS(Kxy) * SQR(n - 2) / SQR(1 - Kxy ^ 2)

PRINT " N", "x", "y", "tx", "ty"

FOR i = 1 TO n

PRINT i, x(i), y(i), tx(i), ty(i)

NEXT i

PRINT "число ответов ="; n

PRINT "табличное значение критерия Стьюдента ="; tt

PRINT "математическое ожидание:"; "по x="; mx, "по y="; my

PRINT "дисперсия:"; "по x="; dx, "по y="; dy

PRINT "среднеквадратическое отклонение:"; "по x="; CKOx, "по y="; CKOy

PRINT "коэффициент вариации:"; "по x="; Vx, "по y="; Vy

PRINT "коэффициент корреляции ="; Kxy

PRINT "рассчитанное значение критерия Стьюдента ="; tr

IF tr >= tt THEN

PRINT "линейная зависимость между x и y Cуществует"

ELSE

PRINT "линейная зависимость между x и y Отсутствует"

END IF

END

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: