Графическое решение задачи

 

Графический метод решения состоит в том, что в одной системе координат строим область допустимых значений для неизвестных величин задачи. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств: х₁=0; х₂=0; ; ; .

Построив полученные прямые, найдем соответствующие полуплоскости допустимых значений переменных и их пересечение. Чтобы определить в каждом случае, какая полуплоскость удовлетворяет данному неравенству, достаточно взять произвольную точку, через которую не проходит соответствующая граничная прямая, и проверить, удовлетворяет ли эта пробная точка ограничению-неравенству. Если удовлетворяет, то данное неравенство выполняется в полуплоскости, содержащей пробную точку. В противном случае берется полуплоскость, не содержащая пробной точки. В качестве пробной точки возьмем точку (10; 10).

 

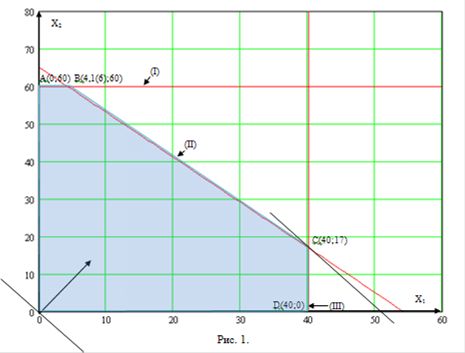
Рис. 1.

радиоприемник оптимальный прибыль предел

Две пары параллельных прямых задают две пересекающиеся полосы, которые в пересечении образуют прямоугольник. Последняя прямая отсекает от этого прямоугольника правый верхний угол, превращая его в пятиугольник ОАВСD, координаты граничных и внутренних точек которого удовлетворяют условию неотрицательности переменных и неравенствам системы ограничений задачи.

Координаты точек пересечения легко установить, и сразу же вычислим значения целевой функции в этих точках:

 

O(0; 0) - F(O)=0,(0; 60) - F(A)=600,(4,1(6), 60) - F(B)=660,(40; 17) - F(С)=770,

D(40; 0) - F(D)=600.

 

Строим нормаль линии уровня 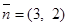 и одну из этих линий, например, 3x₁+2x₂=0.

Так как решается задача на отыскание максимума целевой функции, то линию уровня перемещаем в направлении нормали до опорной линии или точки (Рис. 1). При данных условиях решением будет точка С(40; 17).

Можно было обойтись без нормали и линий уровня, так как доказано, что своего максимума целевая функция достигает в одной из вершин многоугольника ограничений.

Максимальное значение целевой функции равно F(40; 17)=770 в точке (40; 17).

Это означает, что оптимальные суточные объемы производства составляют: радиоприемников первой модели - 40, радиоприемников второй модели - 17. При этом прибыль от реализации произведенных объемов изделий составит 770 условных единиц. Максимальный суточный запас используемых элементов будет израсходован полностью.

 

Решение симплекс методом

 

Получение начального опорного плана

С помощью дополнительных неотрицательных переменных перейдем к системе уравнений:

.

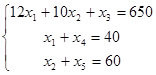Для нахождения первоначального базисного решения разобьём переменные на две группы: основные и неосновные. Так как определитель, составленный из коэффициентов при дополнительных переменных х₃, х₄, х₅ отличен от нуля, то эти переменные можно взять в качестве основных на первом шаге решения задачи. Столбцы коэффициентов при дополнительных переменных представляют собой единичные векторы, которые линейно независимы. Следовательно, соответствующие этим векторам переменные х₃, х₄, х₅ являются базисными.

Разрешим систему уравнений относительно базисных переменных.

Целевую функцию запишем в виде уравнения F(X)=0-(-15х₁-10x₂).

Положим неосновные переменные равными нулю, т.е. х₁=х₂=0, получим первый опорный план .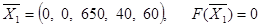

Первый опорный план заносим в симплексную таблицу, которая состоит из коэффициентов системы ограничений и свободных членов. В левом столбце таблицы записываются основные переменные (базис), во втором столбце - свободные члены. Последняя строка таблицы называется индексной и заполняется коэффициентами целевой функции, взятыми с противоположными знаками. Значение целевой функции проставляется в индексной строке в столбце «Значения, базисных переменных». Последний столбец подготовлен для оценочных отношений, необходимых при расчете наибольшего возможного значения переменной. Он обозначен Θ.

Проверка плана на оптимальность Если все коэффициенты индексной строки симплексной таблицы при решении задачи на максимум целевой функции неотрицательны, то план является оптимальным.

Первый опорный план в задаче не оптимальный, так как в индексной строке находятся отрицательные коэффициенты.

Таблица 1.

Базисные переменные	Значения базисных переменных	х1	х2	х3	х4	х5	Θ
х3	650	12	10	1	0	0	54,1(6)
х4	40	1	0	0	1	0	40
х5	60	0	1	0	0	1	∞
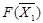
	0	-15	-10	0	0	0	max

 

Определение направляющих столбца и строки

Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине. Направляющий столбец, соответствующий выбранному коэффициенту, показывает, какая переменная на следующем шаге перейдет из свободных в основные (базисные). Так как 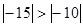, то направляющий столбец соответствует переменной х₁. Элементы столбца значений базисных переменных симплексной таблицы делим на соответствующие положительные коэффициенты направляющего столбца. В результате получаем значения столбца Θ. Из значений столбца Θ выбираем минимальное. Строка симплексной таблицы, соответствующая минимальному значению Θ, является направляющей. Она определяет переменную х₄, которая на следующем шаге выйдет из базиса и станет свободной. На пересечении направляющих столбца и строки находится разрешающий элемент, равный 1.

Определение нового опорного плана

Для перехода к, новому опорному плану производится пересчет симплексной таблицы методом Жордана-Гаусса.

Формируем следующую симплексную таблицу. В левом столбце «Базисные переменные» записываем новый базис: вместо основной переменной х₄ записываем переменную х₁. Строку, соответствующую переменной х₁, получаем путем деления всех элементов строки х₄ первой таблицы на разрешающий элемент, равный 1, то есть она остается без изменения. В остальных клетках столбца х₁ проставляем нули. Все остальные элементы , вычисляем по правилу прямоугольника. Аналогично проводятся расчеты по всем строкам таблицы, включая индексную. Далее возвращаемся к этапу - проверка плана на оптимальность. Выполняя последовательно все этапы алгоритма, заполняем таблицы.

 

Таблица 2.

Базисные переменные	Значения базисных переменных	х1	х2	х3	х4	х5	Θ
х3	170	0	10	1	-12	0	17
х1	40	1	0	0	1	0	∞
х5	60	0	1	0	0	1	60
	600	0	-10	0	15	0	max

 

.

Второй план в задаче тоже не оптимальный, так как в индексной строке еще остается отрицательный коэффициент. Направляющий столбец, соответствующий выбранному коэффициенту, показывает, какая переменная на следующем шаге перейдет из свободных в основные (базисные). Так как, отрицательное число в индексной строке стоит в столбце, который соответствует переменной х₂, то этот столбец будет направляющим. Элементы столбца значений базисных переменных симплексной таблицы делим на соответствующие положительные коэффициенты направляющего столбца. В результате получаем значения столбца Θ. Из значений столбца Θ выбираем минимальное. Строка симплексной таблицы, соответствующая минимальному значению Θ, является направляющей. Она определяет переменную х₃, которая на следующем шаге выйдет из базиса и станет свободной.

Определение нового опорного плана

Для перехода к, новому опорному плану производится пересчет симплексной таблицы методом Жордана-Гаусса. Формируем следующую симплексную таблицу. В левом столбце «Базисные переменные» записываем новый базис: вместо основной переменной х₃ записываем переменную х₂. Строку, соответствующую переменной х₂, получаем путем деления всех элементов строки х₃ первой таблицы на разрешающий элемент. На месте разрешающего элемента в таблице 3 получаем единицу. В остальных клетках столбца х₂ проставляем нули. Все остальные элементы , вычисляем по правилу прямоугольника.

 

Таблица 3.

Базисные переменные	Значения базисных переменных	х1	х2	х3	х4	х5	Θ
х2	17	0	1	0,1	-1,2	0
х1	40	1	0	0	1	0
х5	43	0	0	-0,1	1,2	1
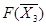
	770	0	0	1	3	0	max

 

На третьем шаге в таблице получен оптимальный план, так как все коэффициенты в индексной строке неотрицательны.

. Используя табличный симплекс метод, получили решение, совпадающее с решением, полученным графическим методом.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: