 |
Задача 3. Определение пределов изменения коэффициентов целевой функции
|
|
|
|
В каких пределах допустимо изменение коэффициентов целевой функции?
Изменение коэффициентов целевой функции, которые определяются ценами на готовую продукцию, оказывает влияние на наклон прямой, которая представляет эту функцию в принятой системе координат. Очевидно, что идентификация конкретной угловой точки в качестве оптимума зависит, прежде всего, от наклона этой прямой.
Это означает, что вариация коэффициентов целевой функции может привести к изменению совокупности связывающих ограничений и, следовательно, статуса того или иного ресурса (т. е. сделать недефицитный ресурс дефицитным, и наоборот). Таким образом, в рамках анализа модели на чувствительность к изменениям коэффициентов целевой функции могут исследоваться следующие вопросы.
· Каков диапазон изменения (увеличения или уменьшения) того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?
· Насколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным и, наоборот, дефицитный ресурс сделать недефицитным?
Обсудим эти вопросы на нашем примере.
Рассматривая первый вопрос, обозначим через с1 и c2 доходы предприятия от продажи одного радиоприемника первой м второй модели соответственно. Тогда целевую функцию можно представить в следующем виде:
.
Из рис. <mk:@MSITStore:C:\DOCUME~1\User\LOCALS~1\Temp\Rar$DI00.938\iop.chm::/part3p3.html>1 видно, что при увеличении c1 или уменьшении c2 прямая, представляющая целевую функцию F, вращается (вокруг точки С) по часовой стрелке. Если же c1 уменьшается или c2 увеличивается, эта прямая вращается в противоположном направлении - против часовой стрелки. Таким образом, точка С будет оставаться оптимальной точкой до тех пор, пока наклон прямой не выйдет за пределы, определяемые наклонами прямых, соответствующих ограничениям (II) и (III).
|
|
|
Когда наклон прямой F станет равным наклону прямой для ограничения (II), получим две альтернативные оптимальные угловые точки С и B. Аналогично, если наклон прямой F станет равным наклону прямой для ограничения (III), будем иметь альтернативные оптимальные угловые точки C и D. Наличие альтернативных оптимумов свидетельствует о том, что одно и то же оптимальное значение F может достигаться при различных значениях переменных. Как только наклон прямой F выйдет за пределы указанного выше интервала, получим некоторое новое оптимальное решение (точка В или точка D).
Чтобы проиллюстрировать сказанное, рассмотрим, каким образом можно найти допустимый интервал изменения с1, при котором точка С остается оптимальной. Исходное значение коэффициента с2=10 оставим неизменным. Из рис. <mk:@MSITStore:C:\DOCUME~1\User\LOCALS~1\Temp\Rar$DI00.938\iop.chm::/part3p3.html>1 видно, что значение с1 можно уменьшать до тех пор, пока прямая F не совпадет с прямой (II), или увеличивать, пока прямая F не совпадет с прямой (III). Эти крайние значения коэффициента с1 можно определить из равенства наклонов прямой F и прямой (III) (максимальное значение с1) и равенства наклонов прямой F и прямой (II) (минимальное значение с1).
Так как тангенс угла наклона для прямой F равен с1/10, а для прямых (II) и (III) соответственно 1.2 и ∞, минимальное значение с1 определяем из равенства 
, а максимальное значение 
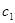находим из равенства 
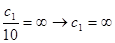.Интервал изменения 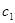, в котором точка С по-прежнему остается единственной оптимальной точкой, определяется неравенством 
.
Аналогично проведем вычисления для приемника второй модели.
Найдем допустимый интервал изменения с2, при котором точка С остается оптимальной. Исходное значение коэффициента с1=15 оставим неизменным. Из рис. <mk:@MSITStore:C:\DOCUME~1\User\LOCALS~1\Temp\Rar$DI00.938\iop.chm::/part3p3.html>1 видно, что значение с2 можно увеличивать до тех пор, пока прямая F не совпадет с прямой (II), или уменьшать, пока прямая F не совпадет с прямой (III). Эти крайние значения коэффициента с2 можно определить из равенства наклонов прямой F и прямой (II) (максимальное значение с2) и равенства наклонов прямой F и прямой (III) (минимальное значение с2).
|
|
|
Так как тангенс угла наклона для прямой F равен 15/с2, а для прямых (III) и (II) соответственно ∞ и 1.2, минимальное значение с2 определяем из равенства 
, а максимальное значение 
находим из равенства 
. Интервал изменения , в котором точка С по-прежнему остается единственной оптимальной точкой, определяется неравенством 
.
Заключение
Имея первоначальные суточные запасы используемых элементов в количестве 650 единиц, суточную производительность первой технологической линии - 40 изделий, суточную производительность второй технологической линии - 60 изделий, для достижения оптимального плана производства необходимо произвести и реализовать 40 радиоприемников первой модели и 17 радиоприемников второй модели. При этом остатков суточных запасов используемых элементов не будет. Сумма от реализации всех выпущенных радиоприемников является при этом максимальной и равна 770 условных единиц. Анализ полученного решения на чувствительность дает следующие результаты:
. Предел увеличения производительности первой технологической линии, превышение которого уже не будет улучшать значение целевой функции равен 54 единицам.
. Предел уменьшения производительности второй технологической линии, при котором полученное оптимальное решение останется неизменным, равен 17 единицам.
. Предел увеличения суточного запаса элементов электронных схем, при превышении которого улучшить значение целевой функции оказывается невозможным, равен 1080 единицам.
. Дефицитным ресурсом, который имеет наибольший приоритет при возможности увеличения ресурсов, является суточный объем производства первой технологической линии.
5. Интервал изменения прибыли от продажи радиоприемника 1-ой модели, в котором оптимально решение остается неизменным, равен 
. 6. Интервал изменения прибыли от продажи радиоприемника 2-ой модели, в котором оптимально решение остается неизменным, равен .
|
|
|
|
|
|
