 |
Вопрос 3. Понятие дисконта и дисконтирования
|
|
|
|
В самом широком смысле дисконт представляет собой разницу между наращенной суммой (S) и первоначальной суммой (Р), т.е. S- P.
Расчет дисконта имеет достаточно важное значение при совершении целого ряда финансовых расчетов. Например, при осуществлении операций с векселями.
Вексель представляет собой особый вид письменного долгового обязательства, дающий его владельцу бесспорное право требовать по истечении указанного в нем срока уплаты денег с должника. При этом в векселе должна указываться только одна - конечная сумма денег.
Векселедержатель (он же кредитор), или владелец других денежных обязательств, в случае необходимости получения денег по векселю или другим долговым обязательствам, ранее указанных в них срока, может продать его банку или другому субъекту по пониженной пене, т.е. по цене ниже той суммы, которая указана на векселе. Такая сделка носит название учета векселя или дисконтирование.
В этом случае дисконтом называется разница между номинальной стоимостью долгового обязательства и суммой, полученной векселедержателем (владельцем векселя) в результате учета векселя.
Дисконт рассчитывается на основе учетной ставки (d). Величина учетной ставки зависит от срока, остающегося до оплаты обязательства и существующих банковских процентных ставок.
В настоящее время термин «дисконтирование» употребляется в финансовом менеджменте весьма широко. Под этим термином может пониматься способ нахождения стоимости величины «Р» на некоторый момент времени, при условии, что в будущем при начислении на нее процентов, она могла бы составить наращенную сумму «S». Величину «Р», найденную дисконтированием наращенной величины «S», называют современной или приведенной стоимостью. С помощью дисконтирования в финансовых вычислениях учитывается также фактор времени.
|
|
|
В финансовых вычислениях выделяют математический и банковский методы дисконтирования.
Математическое дисконтирование (учет)
В финансовой практике часто приходится сталкиваться с задачей, обратной определению наращенной суммы, т.е. по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму Р. При этом под Р понимают как первоначальную сумму, так и сумму на любую другую дату до момента уплаты S. Такая задача возникает, к примеру, тогда, когда проценты удерживаются непосредственно при выдаче ссуд. В этом случае сумма S дисконтируется.
Итак, для определения первоначальной суммы Р по заданным S, n и i из формул S = P (l+ ni) и S = P (1+ i)n выражаем Р:
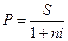 |
- при простых процентах:
при сложных процентах:
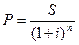 |
Величину Р, если она найдена по S, называют дисконтированной величиной S. Напомним, что ее также называют современной (приведенной, капитализированной) величиной платежа S.
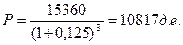 |
Банковское дисконтирование (учет)
Банковский учет используется при операциях с векселями и другими краткосрочными обязательствами (переводом векселей, тратт и т.д.). Суть этой операции заключается в том, что банк или иное финансовое учреждение до наступления срока платежа по векселю покупает его у владельца (векселедержателя) и берет весь риск по получению денег на себя. При этом цена, по которой банк покупает вексель, должна быть меньше той суммы, которая должна быть выплачена по нему в конце срока (т.е. цены, выплачиваемой по векселю, вместе с причитающейся ему частью дисконта).
Итак, получив при наступлении срока деньги по векселю, банк, таким образом, реализует дисконт. Прежний владелец векселя с помощью учета векселя получает деньги ранее указанного в нем срока, т.е. в определенном выигрыше оказываются обе стороны сделки.
|
|
|
При учете векселей банки применяют банковский учет. Согласно этому методу проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды. Применительно к учету векселя это означает, что проценты начисляются на сумму, которую должен выплатить должник в конце срока векселя.
Расчет суммы, получаемой владельцем при учете векселя в банке, производится по формуле:
P=S-Snd =S (1-nd),
где (1- nd) — дисконтный множитель.
Из этой суммы банк может удержать и комиссионные за проведение операции, которые обычно пропорциональны выкупной цене обязательства.
Следует иметь ввиду, что дисконтирование по учетной ставке чаще всего производится при условии, что временная база равна 360 дням, а число дней кредита обычно берется точным.
Пример. Выдана товарная тратта на сумму 2000 д.е. с уплатой 16 ноября. Владелец документа учел ее в банке 23 сентября, при этом учетная ставка составила - 6%. Требуется рассчитать полученную при учете сумму.
Решение;
Так как оставшийся до уплаты срок равен 54 дням, то согласно формуле:
P=S( 1 -nd)
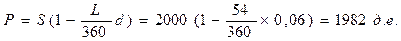 |
имеем:
Все вышеуказанные расчеты касались вексельных операций с использованием простых процентов, но в банковской сфере широко применяются сложные проценты.
Расчет первоначальной суммы по учетной ставке с использованием сложных процентов осуществляется по следующей формуле:
Р = S(1 - d) n
В некоторых случаях возникает необходимость рассчитать наращенную сумму по учетной ставке (при определении цены товара, поставляемого на условиях коммерческого кредита). Формула наращения будет иметь вид:
а) проценты простые
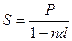
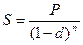 |
б) проценты сложные
|
|
|


